コイルに流れる電流が変化すると、電磁誘導によりコイル自身に発生する現象を「自己誘導」といいます。
コイルに発生する起電力の比例定数を「自己インダクタンス」といいます。
ここでは、自己誘導と自己インダクタンスの説明をします。
自己誘導と自己インダクタンス
自己誘導
コイルに流れる電流の大きさが変化すると、磁束の大きさも変化します。
実はこのときに、コイルの中で不思議なことが起こっています。
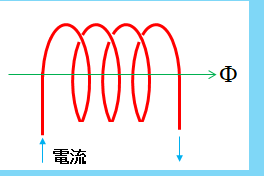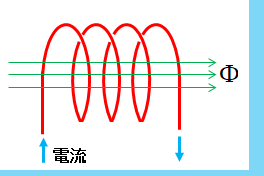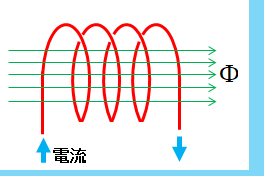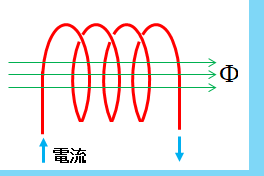
図のようなコイルに電流を \(1\) [A] 流したときに \(1 \Phi\) の磁束が発生したとします。
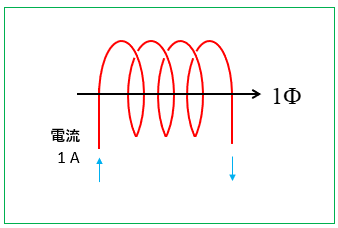
次に電流を \(2\) [A] に増加させるたとき、磁束が \(2 \Phi\) になったとします。
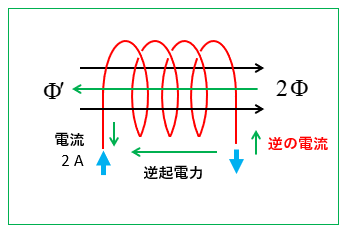
このとき、増加した磁束を減少させようとする磁束 \(\Phi^{\prime}\) が発生します。
この磁束 \(\Phi^{\prime}\) を発生する起電力は、元の起電力に対して逆向きなので 逆起電力 といいます。
磁束 \(\Phi\) が変化することで 電磁誘導作用 により コイル自身に磁束 \(\Phi\) の変化を妨げる現象が起こります。
この現象を 自己誘導 といいます。
自己インダクタンス
また、電流の変化によって、コイル自身に生じる起電力の大きさを表す量のことを
自己インダクタンス といい記号に \(L\) 単位に [H](ヘンリー)を使います。
自己インダクタンスに比例する起電力が発生する
コイルに流れる電流が変化すると、電磁誘導作用により起電力が発生します。
その起電力の方向はレンツの法則によるものです。
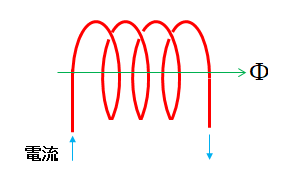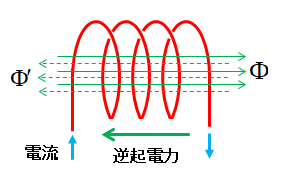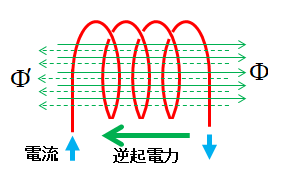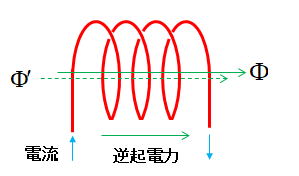
\(\Phi\) はコイルに流れる電流による磁束
\(\Phi^{\prime}\) は逆起電力による磁束
- コイルに流れる電流が増加している時は、磁束 \(\Phi\) が増えているので、磁束 \(\Phi\) を減らす方向の起電力が発生する。
- 逆に、電流が減少している時は、磁束 \(\Phi\) が減っているので、磁束 \(\Phi\) を増やす方向の起電力が発生する。
- コイルに流れる電流の増減により、発生する起電力の向きは反対になる。
■ 磁束鎖交数
N巻のコイルに \(I\) [A] の電流を流したとき
磁束が \(\phi\) [Wb] (ウエーバー)生じたときの
磁束数は \(N\phi\) となり、電流 \(I\) に比例します。
\(L\) は比例定数で、磁束鎖交数を \(\psi\) プシー又はプサイ) で表わすと次のようになります。
\(\psi=N\phi=LI\) [Wb]\(\cdots(1)\)
磁束鎖交数の記号について
磁束鎖交数を \(\Phi\)(ファイ)、\(\psi\)(プシー、プサイ) などで表現している文献があります。
このサイトでは、磁束鎖交数を \(\psi\)(プシー、プサイ)、磁束を \(\Phi\) や \(\phi\) で表示します。
■ 自己インダクタンス
\(L=\cfrac{N\phi}{I}\) [H]
\(L\) を 自己インダクタンス または、単に インダクタンス といいます。
自己インダクタンスの記号は \(L\) で表わし
単位は [Wb/A] ですが 新しい単位 [H] (ヘンリー)を使います。
誘導起電力の大きさは電流の変化率に比例する
自己インダクタンス \(L\) [H] で \(N\) 巻のコイルに流れる電流 \(I\) [A] が流れています。
\(Δt\) 秒間に \(ΔI\) の電流が増加し
磁束が \(Δ\phi\) 増加したとき、磁束の変化量は \(NΔ\phi\) です。
\(\psi=N\phi=LI\) [Wb]\(\cdots(1)\)
式(1)から、次の式が成り立ちます。
\(NΔ\phi=LΔI \cdots(2)\)
コイル(自己インダクタンス)に誘導される起電力は ファラデーの法則 により
ファラデーの法則
\(e=-N\cfrac{Δ\phi}{Δt}\)\(\cdots(3)\)
式(2)を式(3)に代入すると
自己誘導起電力
\(e=-L\cfrac{ΔI}{Δt}\)\(\cdots(4)\)
誘導される起電力は ー(マイナス) で表されます。
\(e=-L\cfrac{ΔI}{Δt}\) [V] または
\(e=-L\cfrac{dI}{dt}\) [V]
練習問題
問題1
コイルに流れる電流が 2秒間に \(0\) [A] から \(1\) [A] に変化しました。
コイルに発生する自己誘導起電力 \(e\) [V] を求めよ。
ただし、コイルの自己インダクタンス \(L\) を \(60\) [mH] とします。
<解答例>
コイルの自己インダクタンスの単位を揃えます。
\(L=60\) [mH] = \(60×10^{-3}\) [H]
自己誘導起電力の公式に代入します。
\(e=-L\cfrac{ΔI}{Δt}=-60×10^{-3}×\cfrac{1}{2}=-0.03\) [V]
\(e=-0.03\) [V] になります。
以上で「自己誘導と自己インダクタンス」の説明を終わります。