コイル回路の電圧と電流の波形図や、ベクトル図の表示方法を説明します。
コイル回路の表示
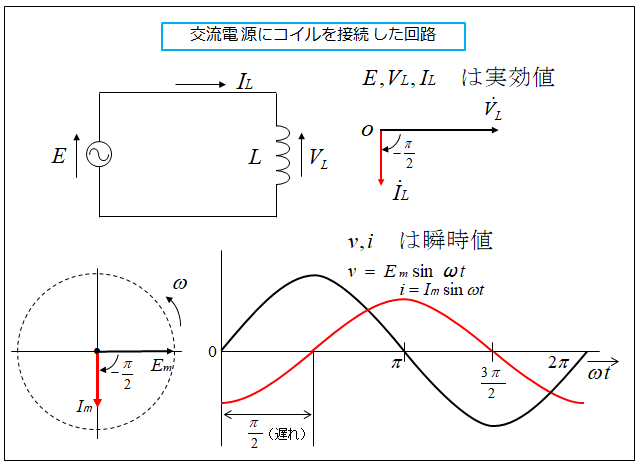
交流電源にコイルを接続した回路の場合、図のように表すことができます。
■ 表示方法の一覧

電流を基準にした回転ベクトルと電流・電圧波形
電流 \(i\) を基準にした回転ベクトルと電流と電圧の波形を示すと図のようになります。
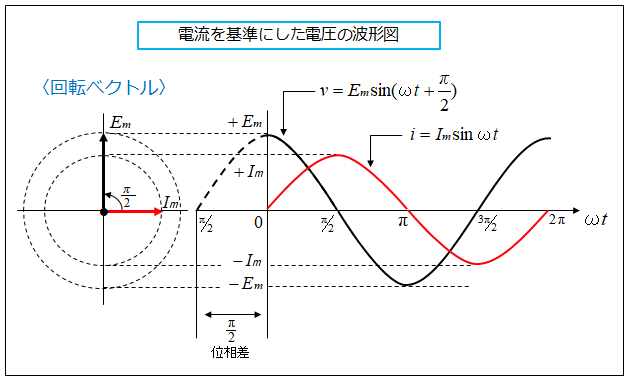
電流を基準にした電流・電圧波形の関係
コイル(自己インダクタンス) \(L\) に
誘導される電圧 \(V\) は 電流 \(i\) より
位相が \(\cfrac{π}{2}\) [rad] 進んでいます。
電圧の正負と電流の増減の関係
- 電圧が正(プラス)にある「\(0\) から \(\cfrac{π}{2}\) の間」は、電流は増加しています。
- 電圧が負(マイナス)にある「\(\cfrac{π}{2}\) から \(\cfrac{3π}{2}\) の間」は、電流は減少しています。
これは、コイルに誘導される電圧が、レンツの法則 によるためです。
電流が増加している時は、電流の増加を妨げるように
電流が減少している時は、電流の減少を妨げるように働くためです。
この誘導電圧が電源の電圧とつり合っていることになります。
電流を基準にした、電流・電圧の瞬時値の表示方法
電流 (i\) を基準にするとその瞬時値 \(i\) は次のとおりです。
\(i=I_m\sinωt\) [A]
電圧 \(v\) は図のように
電流 \(i\) より位相が
\(\cfrac{π}{2}\) [rad] 進んでいるので
その瞬時値 \(v\) は次のとおりです。
\(v=E_m\sin(ωt+\cfrac{π}{2})\) [V]
電圧を基準にした回転ベクトルと電圧・電流波形
電圧 \(v\) を基準にした回転ベクトルと電圧と電流の波形を示すと図のようになります。
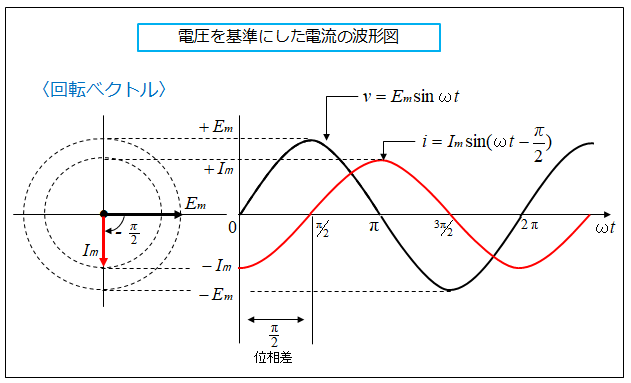
■ 電圧を基準にした電圧・電流波形の関係
次に、コイル(自己インダクタンス \(L\) に誘導される電圧 \(v\) を基準にすると、
電流 \(i\) は、位相が \(\cfrac{π}{2}\) [rad] 遅れています。
進みと遅れは、電流を基準にするか
または、電圧を基準にするかで異なるわけですから、相対的なものになります。
■ 電圧を基準にした、電圧・電流の瞬時値の表示方法
電圧 \(v\) を基準にするとその瞬時値 \(v\) は次のとおりです。
\(v=E_m\sinωt\) [A]
電流 \(i\) は図のように、電圧 \(v\) より
位相が \(\cfrac{π}{2}\) [rad] 遅れているので
その瞬時値 \(i\) は次のとおりです。
\(i=I_m\sin(ωt-\cfrac{π}{2})\) [A]
コイル回路の電圧・電流のベクトル表示
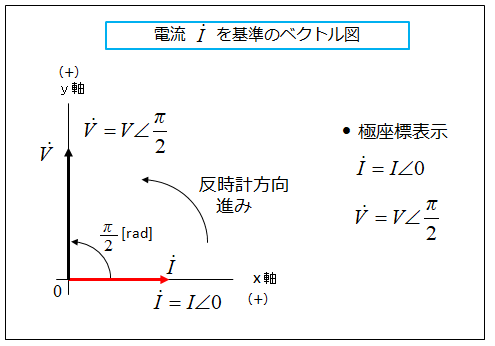
■ 電流を基準にした場合
コイル(自己インダクタンス)に
誘導される電圧のベクトル \(\dot{V}\)
電流のベクトル \(\dot{I}\) とすると、
電圧の位相は電流より \(\cfrac{π}{2}\) [rad] 進んでいます。
極座標表示で表すと次のようになります。
\(\dot{I}=I∠0\)
\(\dot{V}=V∠\cfrac{π}{2}\)
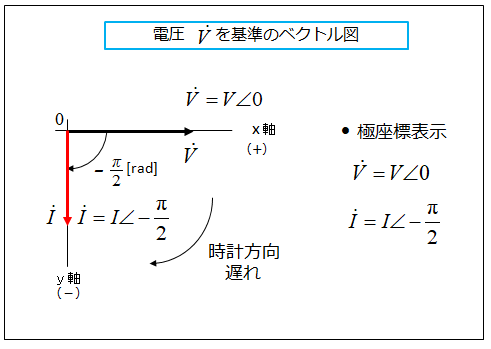
■ 電圧を基準にした場合
基準を変えて、電圧 \(\dot{V}\) を基準のベクトルにして見ると、
電流の位相は電圧より \(\cfrac{π}{2}\) [rad] 遅れています。
極座標表示で表すと次のようになります。
\(\dot{V}=V∠0\)
\(\dot{I}=I∠-\cfrac{π}{2}\)
コイル回路のオームの法則
交流回路において、コイルは電流の流れを妨げる働きをします。
これは抵抗回路の抵抗に相当するものです。
この電流の流れを妨げる \(X_L\) を
「誘導リアクタンスまたは、誘導性リアクタンス」といいます。
単位は抵抗と同じで [Ω](オーム を使います。

練習問題
問題1
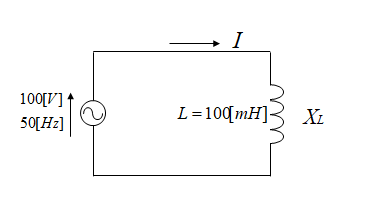
インダクタンス \(L\) が 100 [mH] のコイルに 50 [Hz]
100[V] の交流電圧を加えたときの誘導性リアクタンス \(X_L\) と電流を求めよ。
ただし、\(π=3.14\) とする。
<解 答>
誘導性リアクタンス \(X_L\) は
\(X_L=ωL=2πfL\)\(=2×3.14×50×100×10^{-3}\)
\(X_L=31.4\) [Ω]
流れる電流 \(I\) は
\(I=\cfrac{V}{X_L}=\cfrac{100}{31.4}\)
\(I≒3.18\) [A]
以上で「コイル回路の電圧と電流の表示方法」の説明を終わります。