コイルに電流を流すと、コイルには磁気エネルギーが貯まります。
また、コイルに流れる電流は、位相が90度遅れます。
ここでは、コイルに貯まるエネルギーと電流が遅れについて説明します。
コイルに蓄えられるエネルギーの公式
自己インダクタンス \(L\) [H] のコイルに
電流 \(I\) [A] が流れたときに
コイルに蓄えられるエネルギーの公式は、次のようになります。
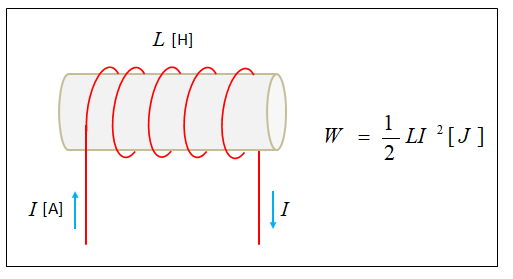
コイルに蓄えられるエネルギーの公式
\(W=\cfrac{1}{2}LI^2\) [J]
- \(W\) [J]\(\cdots\)コイルに蓄えられる電磁エネルギー
- \(L\) [H]\(\cdots\)コイルの自己インダクタンス
- \(I\) [A]\(\cdots\)コイルに流れる電流
公式の求め方
\(W=\cfrac{1}{2}LI^2\) [J] の求め方。
電荷 \(Q\) [C] の持つ位置エネルギー\(U\) [J] は
\(U=QV\) [J]\(\cdots(1)\) になります。
ファラデーの法則から \(e=-L\cfrac{Δi}{Δt}\) [V]
自己インダクタンス \(L\) [H] に発生する起電力の大きさ \(V\) は
\(V=L\cfrac{I}{t}\) [V]\(\cdots(2)\)
電流の定義は、単位時間あたりの電荷量になります。
\(I=\cfrac{Q}{t}\) [A]
\(t\) 秒間に \(I\) [V] まで
一定の大きさで増加すると
電荷量 \(Q\) [C] は図の三角形の面積になります。
\(Q=\cfrac{1}{2}It\) [C]\(\cdots(3)\) になります。
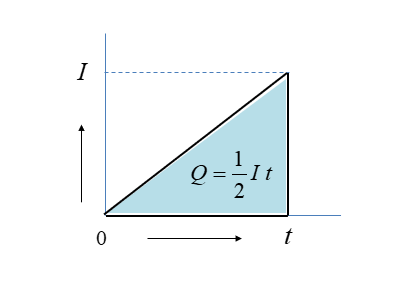
式(1)に式(2)と式(3)を代入します。
\(U=QV=\cfrac{1}{2}It×L\cfrac{I}{t}=\cfrac{1}{2}LI^2\) [J]
コイルに蓄えられるエネルギーを \(W\) とすると
\(\large W=\cfrac{1}{2}LI^2\) [J] となります。
コイルに流れる電流が90°遅れるわけ
コイルに流れる電流が90°遅れるわけ
三角関数で誘導起電力と電流の位相を計算します。
位相の進みと遅れは基準にするもので違う。
電流を基準に、起電力の大きさを考えます。
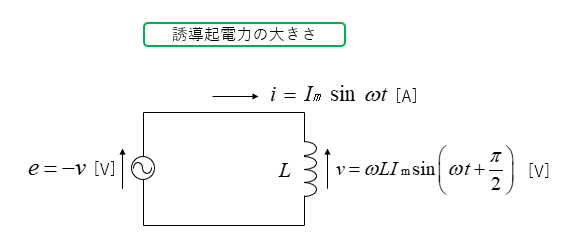
コイルに流れる電流の瞬時値は
\(i=I_m\sinωt\) [A] です。
コイルに誘導される、起電力は ファラデーの法則 により、電流の変化率に比例します。
\(v=L\cfrac{Δi}{Δt}\cdots(1)\)
電流の変化率
図において、コイルに流れる電流の瞬時値 \(i_1\) は
\(i_1=I_m\sinωt \cdots(2)\)
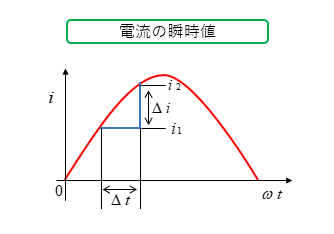
時間が \(Δt\) [S] 経過したときの電流 \(i_2\) は
\(i_2=I_m\sin(ωt+ωΔt) \cdots(3)\)
電流の変化分 \(Δi\) は
\(Δi=i_2-i_1 \cdots(4)\)
式(4)に式(2)と式(3)を代入します。
\(Δi=i_2-i_1 \cdots(4)\)
\(Δi=I_m\sin(ωt+ωΔt)-I_m\sinωt\)\(\cdots(5)\)
式(5)の \(\sin(ωt+ωΔt)\) を三角関数の加法定理で展開すると
加法定理 \(\sin(α+β)=\sinα\cosβ+\cosα\sinβ\) ですから
\(\sin(ωt+ωΔt)\)\(=\sinωt\cosωΔt+\cosωt\sinωΔt\)\(\cdots(6)\)
ここで、\(Δt\) が非常に小さい時間の場合は
\(\cosωΔt≒\cos0=1\)
\(\sinωΔt≒ωΔt\) になります。
これを、式(6)に代入します。
\(\sin(ωt+ωΔt)\)\(≒\sinωt×1+\cosωt×ωΔt\)
\(\sin(ωt+ωΔt)\)\(≒\sinωt+\cosωtωΔt\)\(\cdots(7)\)
式(7)を式(5)に代入すると、次のようになります。
\(Δi=I_m\sin(ωt+ωΔt)-I_m\sinωt\)\(\cdots(5)\)
\(Δi=I_m(\sinωt+\cosωtωΔt)-I_m\sinωt\)
\(Δi=I_m\sinωt+I_m\cosωtωΔt-I_m\sinωt\)
\(Δi=ωΔtI_m\cosωt \cdots(8)\)
初めの誘導起電力の式(1)に式(8)を代入すると
\(v=L\cfrac{Δi}{Δt}\)\(\cdots(1)\)
\(v=L\cfrac{ωΔtI_m\cosωt}{Δt}\)
\(v=ωLI_m\cosωt \cdots(9)\)
三角関数の公式から、\(cosθ=sin(θ+\cfrac{π}{2})\) なので、式(9)は
\(v=ωLI_m\sin(ωt+\cfrac{π}{2})\cdots(10)\)
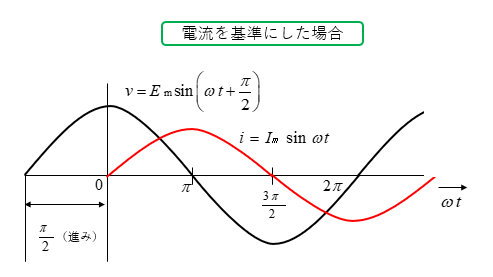
式(10)を見れば分かる通り、誘導起電力 \(v\) は電流 \(i=I_m\sinωt\) より
位相が \(\cfrac{π}{2}\) [rad] 進んで います。
逆にいえば、電流 \(i\) は電圧 \(v\) より位相が \(\cfrac{π}{2}\) [rad] 遅れて いることになります。
導される起電力 \(v\) は電源電圧 \(e\) と釣り合うことになります。
非常に小さい角度の三角関数
いま、図のような半径1 の円を考えるたとき
角度 \(θ\) ラジアン に対する、円弧の長さは \(θ\) です。
\(\sinθ\) は 赤線の長さ、\(\cosθ\) は 青線の長さ になる。
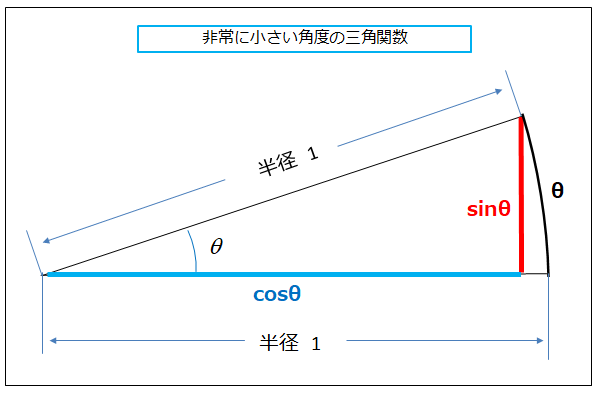
従って、角度 θ の値が 0(ゼロ)に近づいて行くと
\(θ→0\) のとき \(\sinθ→θ\) (赤線の長さは、円弧の長さに近づいて行く)
\(\cosθ→1\) 青線の長さは、円の半径の1 に近づいて行く)
\(\tanθ→θ\) \((\tanθ=\cfrac{\sinθ}{\cosθ}=\cfrac{θ}{1}=θ)\)
\(\cosωΔt≒\cos0=1\)
\(\sinωΔt≒ωΔt\)
位相の進みと遅れの基準
位相の進みと遅れは相対的なものですから、電圧を基準にした場合と電流を基準にした場合では、見方が逆になります。
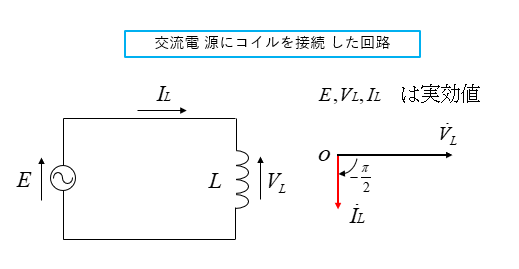
■ 電流を基準にした場合
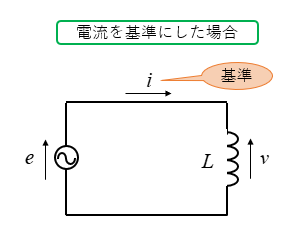
交流電源にコイルを接続した回路の場合、電流に対して、電圧が \(\cfrac{π}{2}\)(90°)進みます。
■ 電圧を基準にした場合
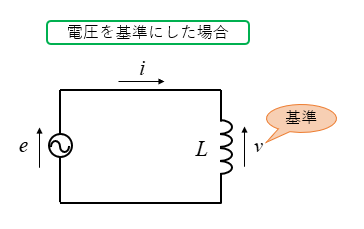
交流電源にコイルを接続した回路の場合、電圧を基準にすれば、電圧に対して、電流が \(\cfrac{π}{2}\)(90°)遅れます。

以上で「コイルに貯まるエネルギーと電流の位相が遅れるわけ」の説明を終わります。