相互誘導とは、磁気的に接続された二つのコイルにおいて
一つのコイルの電流が変化することで、もう一方のコイルに起電力が発生する現象をいいます。
相互インダクタンスとは、一次コイルと二次コイルの相互間の比例定数をいいます。
発生する起電力の大きさは、コイルの形状、大きさ、相互の位置などによる比例定数 M によって決まります。
この比例定数 M を相互インダクタンスといい、単位には自己インダクタンスと同じ [H] (ヘンリー) を使います。
相互誘導と相互インダクタンス
相互誘導
図のように、磁気的に結合されている磁気回路において、一次コイルに交流電流を接続すると磁束が変化するので、二次コイルに交流起電力が発生します。
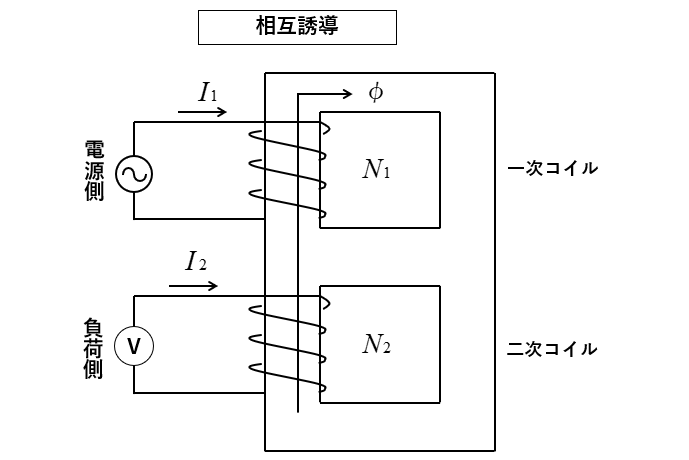
一次コイルの電流が \(Δt\) 秒間に \(ΔI\) [A] 変化して
磁束 \(Δ\phi\) [Wb] だけ変化した時の二次側の誘導起電力 \(e_2\) [V] は
二次コイルの巻数を \(N_2\) とすると
相互誘導起電力は
\(e_2=-N_2\cfrac{Δ\phi}{Δt}\)\(\cdots(1)\)
相互インダクタンス
ま\(e_2\) [V] は \(\cfrac{ΔI}{Δt}\) に比例するので
比例定数を \(M\) とすると
相互誘導起電力は
\(e_2=-M\cfrac{ΔI}{Δt}\)\(\cdots(2)\)
式(1)と式(2)から
\(N_2\cfrac{Δ\phi}{Δt}\)\(=M\cfrac{ΔI}{Δt}\)
\(N_2Δ\phi\)\(=M{ΔI}\) から
相互インダクタンスは
\(M=N_2\cfrac{Δ\phi}{ΔI}\) [H] になります。
相互インダクタンスと自己インダクタンスの関係
コイル1の電流によって、作られる磁束を \(\phi_1\)
コイル2の電流によって、作られる磁束を \(\phi_2\) とします。
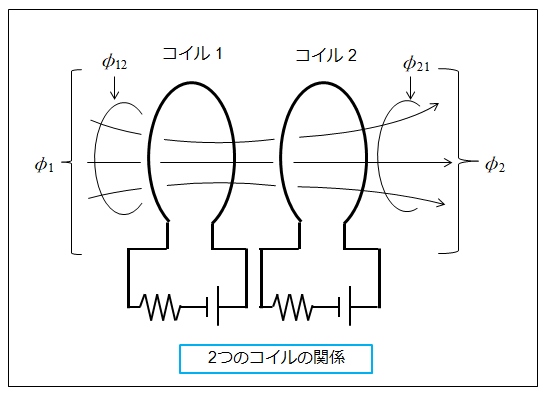
コイル1の磁束 \(\phi_1\) が
コイル2 と鎖交する磁束を \(\phi_{21}\) とすると
\(M_2=\cfrac{\phi_{21}}{I_1}\)
コイル2の磁束 \(\phi_2\) がコ
イル1と鎖交する磁束を \(\phi_{12}\) とすると
\(M_1=\cfrac{\phi_{12}}{I_2}\)
相互インダクタンスを \(M\) とすると
\(M=M_{21}=M_{12}\) となります。
コイル1 の自己インダクタンスを \(L_1\)
コイル2 の自己インダクタンスを \(L_2\) とすると
\(L_1=\cfrac{\phi_1}{I_1}\) [H]
\(L_2=\cfrac{\phi_2}{I_2}\) [H]
コイル1 の作る磁束が全てコイル2に交わるのであれば
\(\phi_1=\phi_{21}\) であり、 \(\phi_2=\phi_{12}\) が成立します。
\(M^2=\cfrac{\phi_{21}\phi_{12}}{I_1I_2}\)\(=\cfrac{\phi_1\phi_2}{I_1I_2}=L_1L_2\)
\(M=\pm\sqrt{L_1L_2}\) となります。
一般には、磁気的に完全に結合することはないので
\(\phi_1>\phi_{21}、\phi_2>\phi_{12}\) となります。
\(M=\pm k\sqrt{L_1L_2} (0≦k≦1)\)
相互インダクタンスの公式
\(M=\pm k\sqrt{L_1L_2} (0≦k≦1)\)
- \(k\):結合係数 (0~1)
- \(M\) [H] :相互インダクタンス
- \(L\) [H] :自己インダクタンス
コイルの接続方法(和動接続と差動接続)
二つのコイルを磁気的に接続した時、和動接続と差動接続があります。
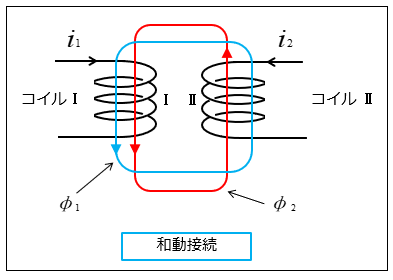
■ 和動接続
和動接続は、二つのコイルの磁束が互いに加わりますので、合成インダクタンスは
\(L=L_1+L_2+2M\) [H]
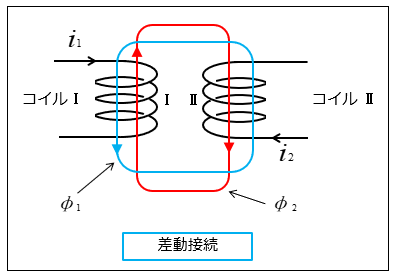
■ 差動接続
差動接続は、二つのコイルの磁束が互いに打ち消し合うので、合成インダクタンスは
\(L=L_1+L_2-2M\) [H]
以上で「相互誘導と相互インダクタンス」の説明を終わります。