電気回路の 電圧、電流、抵抗、電力の関係を説明します。
電圧、電流、抵抗はオームの法則に関係します。
電力は電圧と電流の積になります。
電圧、電流、抵抗、電力の関係
電熱器を例にして 電圧、電流、抵抗、電力の関係を考えてみましょう。
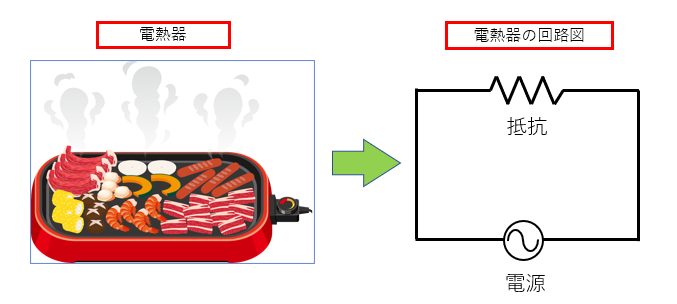
電熱器が加熱されるのは、ニクロム線などの抵抗に電流が流れることで
電流の三大作用 の一つである 電流の発熱作用 により熱が発生するからです。
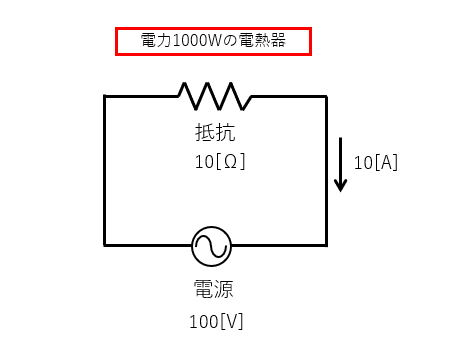
次の図のような、抵抗が 10 [Ω] (オーム) の
電熱器を 100 [V] (ボルト) の電源に接続すると
回路には 10 [A] (アンペア) の電流が流れます。
このときの消費電力は 1000 [W] (ワット) になります。
オームの法則
■ 記号の説明
抵抗は記号に \(R\)、単位に [Ω] (オーム)
電流は記号に \(I\)、単位に [A] (アンペア)
電圧は記号に \(E\)、単位に [V] (ボルト)
電力は記号に \(P\)、単位に [W] (ワット)を使います。
抵抗 \(R\) 、電流 \(I\) 、電圧 \(E\) の間には
電気回路の基礎になる オームの法則 があります。
オームの法則
\(I=\cfrac{E}{R}\)
★ 電熱器の図でそれぞれの関係を見てみると、次のようになります。

回路に流れる電流の大きさは
電圧と抵抗の大きさがわかれば求めることができます。
\(I=\cfrac{E}{R}=\cfrac{100}{10}=10\) [A]
回路の抵抗の大きさは
電圧と電流の大きさがわかれば求めることができます。
\(R=\cfrac{E}{I}=\cfrac{100}{10}=10\) [Ω]
回路の電圧の大きさは
電流と抵抗の大きさがわかれば求めることができます。
\(E=R×I=10×10=100\) [V]
電力を求める公式
電力 \(P\) を求める公式は、次のようになります。
\(P=EI\) [W]
電力の大きさは、電圧と電流の大きさがわかれば求めることができます。
\(P=E×I=100×10=1000\) [W]
電力の大きさは、抵抗と電流の大きさがわかれば求めることができます。
\(P=EI=RI×I=R×I^2=10×100=1000\) [W]
電力の大きさは、電圧と抵抗の大きさがわかれば求めることができます。
\(P=EI=E×\cfrac{E}{R}=\cfrac{E^2}{R}=\cfrac{10000}{10}=1000\) [W]
電気製品の電力
電気製品には消費電力が表示されています。
電気製品の消費電力がわかると
その電気製品に流れるおおよその電流を知ることができます。
家庭用のコンセントに来ている電気の電圧は \(100\) [V] です。
たとえばテレビの消費電力が \(100\) [W] であるならば
電力の公式から
\(P=E×I\)より
\(I=\cfrac{P}{E}=\cfrac{100}{100}=1\) [A]
のように求めることができます。
電力については、直流と交流では求め方が異なる場合があります。
ここでは電力を単純に電圧と電流の積として説明しています。
以上で「電気回路ーよく分かる抵抗、電流、電圧、電力の関係」の説明を終わります。