豆電球を電池につないだ回路で電圧、電流、抵抗の関係を説明します。
豆電球と電池をつないだ回路です。
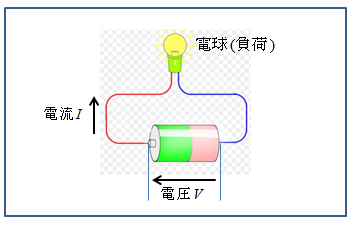
電気回路としては、最も簡単な回路で懐中電灯の回路でもあります。
この回路で電圧、電流、抵抗の関係を説明します。
電圧、電流、抵抗の関係でオームの法則を説明します。
電流について
電池に豆電球をつなぐと、導線に電流が流れて豆電球が光ります。
最も簡単な電気回路ですが、この回路によって電圧・電流・抵抗の関係を知ることができます。

- 電池は電圧
- 電流は回路に流れるもの
- 電球は抵抗で負荷(ふか)といいます。
電流の向き
電流が流れる導線の中では電子が移動しています。
この電子が移動することで電流が流れます。
図のように、電子の流れる向きと電流の流れる向きは逆向きになります。
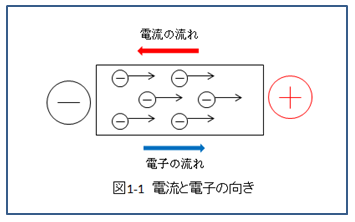
電子の流れる向きと電流の流れる向きは逆向きになります。
これは電流と電子の発見時期による歴史的な事情によるものです。
- 電磁気学の初期の頃、正の電気の粒(電子)の流れを電流と呼ぶことにしました。
- そして、電流は+(プラス)から-(マイナス)に流れることに決めました。
- 後になって電子は負の電気を持つことが判明したのです。
つまり、電流と電子の流れは向きが反対だったということがあとから分かったのです。
この頃になると、電磁気学は確立されていたので、いまさら電流の流れの向きを変えることはできませんでした。
そこで、電流は電子の流れと反対の向きに流れると定義したのです。
電流の大きさ
電流とは電気の粒(電荷)の流れであり、電流の大きさは電気の粒(電荷)の密度になります。
電流の単位は \(\rm A\) (アンペア)です。
\(1\) [A] とは、ある断面に1秒間に1 [C](クーロン、電気の粒の単位)の電荷が流れると定義されています。
数式で表すと、電流の定義は次のように表わせます。
\(I=\cfrac{Q}{t}\) [A]
- \(I\) [A] は電流
- \(Q\) [C] は電荷
- \t(\) [s] は時間
電圧について
水道の蛇口から水が出るのは、水圧がかかっているからです。
同じように、電気回路に電流が流れるには電流を流すための圧力、つまり電圧が必要です。
電流を流すための圧力である電圧の性質は、水の圧力と同じように考えることができます。
水槽を例にして、圧力(電圧) を考えて見ましょう。
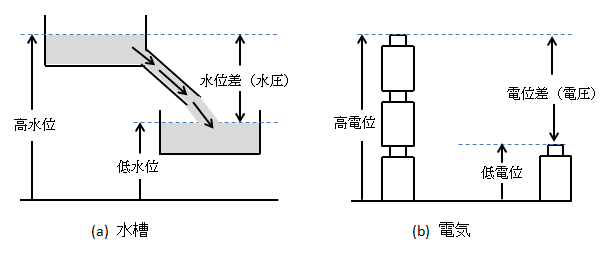
(a)のように、水槽に高低差がある時は、水位の 「高い所」から「水位の低い所」 へ水が流れます。
(b)のように電池に置き変えて考えると、電圧(電位)の高い方から低い方へ電流が流れます。
しかし、(c)のように同じ水位の場合は、ABの水槽に水の流れは起きません。

これは電気の場合も同じで同電位(電圧が同じ)の場合は電流の流れは起きません。
- 電気の世界では、この「水位」に対応するものを「電位」といいます。
- 電位間の差のことを電位差といい、この電位差のことを単に電圧と呼んでいます。
電圧の表わし方と基準点
電圧は各点の電位の差のことですから、基準点をどこに取るかによって大きさが変わってきます。
例えば、次の図のように 基準点をゼロ の所にする
- a点の電圧は1.5Vになる。
- b点の電圧は3Vになる。
- c点の電圧は4.5Vになる。
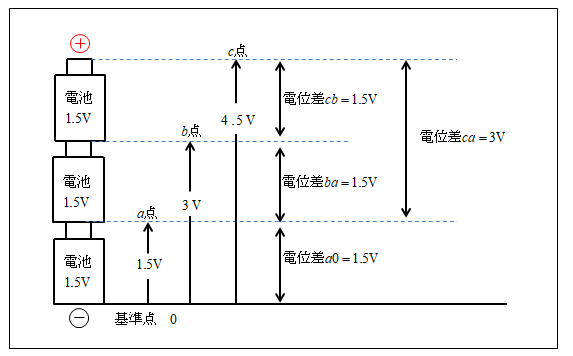
また、図のように「基準点」をa点の所にすると
- 0点の電圧は-1.5Vになる。
- b点の電圧は1.5Vになる。
- c点の電圧は3Vになる。
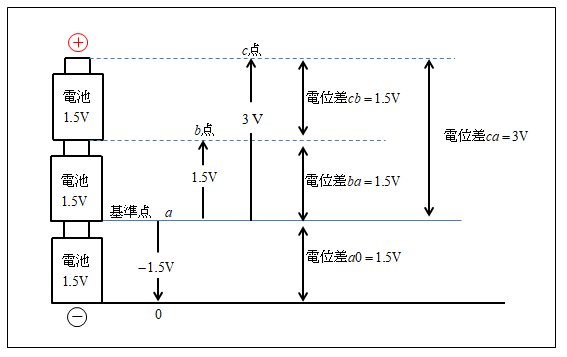
このように、基準点をどこにするかによって、各点の電圧は変わってきます。
負荷とオームの法則
最も簡単な電気回路でつないだ電球に、電流を流すと電球は光ります。
これは電気エネルギーが、光のエネルギーに変化した訳です。
負荷のことを抵抗という
実際にはこの時には光だけでなく、熱としてもエネルギーが使われています。
電気のエネルギーを消費して、仕事をするものを負荷(ふか)といいます。
この電球のような負荷を、電気抵抗または単に抵抗と呼んでいます。

- 抵抗は \(R\)
- 電流は \(I\)
- 電圧は \(V\) で表わします。
これら電流 \(I\)、電圧 \(V\)、抵抗 \(R\) の間には次のような関係が成り立ちます。
\(I=\cfrac{V}{R}\)
この関係式のことをオームの法則といいます。
オームの法則
- 電流の大きさは、電圧の大きさに比例する。
- 電流の大きさは、抵抗の大きさに反比例する。
ということを示す法則で、電気の最も基本になるものです。
抵抗の接続
抵抗の直列接続
(a) のような抵抗の接続方法を抵抗の直列接続といいます。
\(R_1\) と \(R_2\) を流れる電流 \(I\) は同じ大きさです。
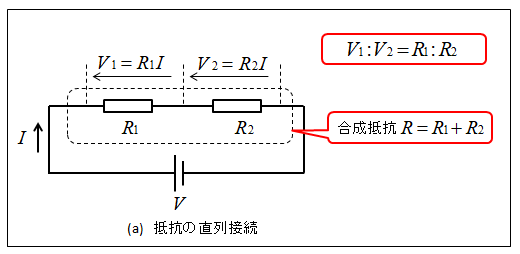
各抵抗の端子間電圧を \(V_1、V_2\) とすると、オームの法則から
\(V=V_1+V_2\)
\(V=R_1I+R_2I\)
\(V=(R_1+R_2)I\) となり、合成抵抗を \(R\) とすれば、\(R=R_1+R_2\) になります。
- 2個以上の抵抗を直列に接続した場合も、同様に計算することができる。
- 多数の抵抗を直列に接続した場合の合成抵抗は、それぞれの抵抗の和で求められます。
- この時の各抵抗にかかる電圧の大きさは、各抵抗の大きさに比例します。
\(R_1:R_2=V_1:V_2\) となります。
このことを抵抗による電圧の分圧といいます。
抵抗の並列接続
(b)のように抵抗を接続する方法を抵抗の並列接続といいます。
\(R_1\) と \(R_2\) にかかる電圧 \(V\) は同じ大きさです。
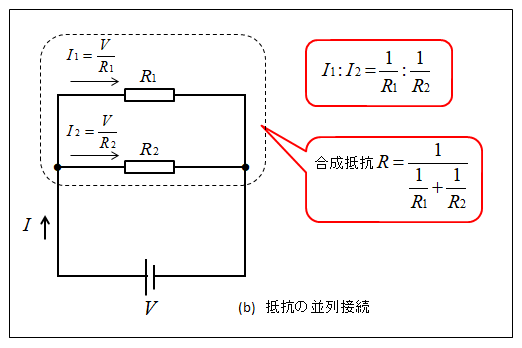
各抵抗に流れる電流を \(I_1、I_2\) とすると、オームの法則から
\(I=I_1+I_2\)
\(I=\cfrac{V}{R_1}+\cfrac{V}{R_2}\)
\(I=\left( \cfrac{1}{R_1}+\cfrac{1}{R_2} \right)V\) になります。
合成抵抗を \(R\) とすれば
\(\cfrac{1}{R}=\cfrac{1}{R_1}+\cfrac{1}{R_2}\)
\(R=\cfrac{1}{\cfrac{1}{R_1}+\cfrac{1}{R_2}}\) になります。
- 2個以上の抵抗を並列に接続した場合も、同様に計算することができる。
- 多数の抵抗を並列に接続した場合の合成抵抗は、それぞれの抵抗の逆数の和で求められます。
- この時の各抵抗に流れる電流の大きさは、各抵抗の大きさの逆数に比例します。
\(\cfrac{1}{R_1}:\cfrac{1}{R_2}=I_1:I_2\) となり、電源からの電流 \(I\) を \(\cfrac{1}{R_1}:\cfrac{1}{R_2}\) に分ける働きをします。
このことを抵抗による電流の分流といいます。
電圧降下の表わし方
電気回路の抵抗に、電流が流れると電圧降下が起こります。
抵抗での電圧降下の表わし方には、決まりがあります。
抵抗での電圧降下は、その抵抗を流れる電流の向きと逆向きの起電力で表現される。


練習問題
問題1
100Ωの抵抗に10Vの電圧を加えた時に流れる電流を求めよ。

<解 答>
オームの法則から
\(I=\cfrac{V}{R}=\cfrac{10}{100}=0.1\quad\rm[A]\)
問題2
次の回路に 10V の電圧を加えたとき、0.2A の電流が流れた。抵抗 R の値を求めよ。
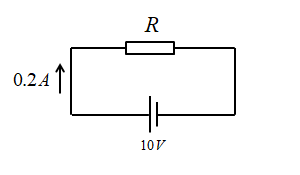
<解 答>
オームの法則から
\(R=\cfrac{V}{I}=\cfrac{10}{0.2}=50\quad\rm[Ω]\)
問題3
200Ω の抵抗に 0.5A の電流が流れている、この時の抵抗の両端の電圧 V を求めよ。

<解 答>
オームの法則から
\(V=I×R=0.5×200=100\quad\rm[V]\)
問題4
次の回路(a)、(b)、(c)、(d)の各回路の合成抵抗を求めよ。
ただし、\(R_1=10\quad\rm[Ω]\)、\(R_2=20\quad\rm[Ω]\)、\(R_3=40\quad\rm[Ω]\) とする。

<解 答>
(a)
\(R=R_1+R_2+R_3=10+20+40=70\quad\rm[V]\)
(b)
\(\cfrac{1}{R}=\cfrac{1}{R_1}+\cfrac{1}{R_2}+\cfrac{1}
{R_3}\)\(=\cfrac{1}{10}+\cfrac{1}{20}+\cfrac{1}{40}\)\(=\cfrac{7}{40}\)
\(R=\cfrac{40}{7}\quad\rm[Ω]\)
(c)
\(\cfrac{1}{R}=\cfrac{1}{R_1+R_2}+\cfrac{1}{R_3}\)\(=\cfrac{1}{10+20}+\cfrac{1}{40}\)\(=\cfrac{7}{120}\)
\(R=\cfrac{120}{7}\quad\rm[Ω]\)
(d)
\(R=R_1+\cfrac{1}{\cfrac{1}{R_2}+\cfrac{1}{R_3}}\)\(=10+\cfrac{1}{\cfrac{1}{20}+\cfrac{1}{40}}\)\(=10+\cfrac{40}{3}\)\(=\cfrac{70}{3}\quad\rm[Ω]\)
問題5
10s(秒)間に70C(クーロン)の電気量が流れました。
電流が均一に流れているものとしたとき、流れている電流を求めよ。
<解 答>
電流は1秒間に流れる電気量で表されます。
\(I=\cfrac{Q}{t}\quad\rm[A]\) より
\(I=\cfrac{70}{10}=7\quad\rm[A]\)
問題6
6 A(アンペア)の電流が 12s(秒)間流れています。移動した電気量を求めよ。
また電気はすべて電子によって運ばれているものとすると、移動した電子の個数はおよそ何個か求めよ。
電子1個の持つ電荷量 \(q\) は\(q=-1.602×10^{-19}\hspace{8px}\rm [C]\) とします。
<解 答>
\(I=\cfrac{Q}{t}\) を変形して
\(Q=It=6×12=72\quad\rm[C]\)
移動した電子の数 \(n\)
\(n=\cfrac{Q}{q}≒44.9×10^{19}\) 個
以上で「最も簡単な電気回路」の説明を終わります。