ここでは、直流回路の電力と電力量の求め方を説明します。
直流回路の電力と電力量は、簡単に求めることができます。
電力量は電気エネルギーがする仕事量
電気スタンドに電流が流れると光が発生し、周囲を明るく照らすことができます。
これは電気エネルギーが光エネルギーに変換され、周囲を明るくするという仕事をしたことになります。

その他、電気エネルギーは熱に変換したり、モーターなどで動力に変換したりすることができます。
電流1アンペアは、1秒間に1クーロンの電荷が移動することです。
式で表すと
\(I=\cfrac{Q}{t}\) [A]
したがって、\(t\) 秒間に \(I\) アンペアの電流が流れるとその電気量 \(Q\) は
\(Q=I×t\) クーロンになります。
電力量 \(W\) は 電圧(電位差) \(V\) のところを、電気量 \(Q\) クーロンが移動した仕事量(ジュール)になりますので、
\(W=VQ=VIt\) [J] になります。
直流回路の電力と電力量
電力は記号を \(P\)、単位を \(\rm [W]\) ワット)
電力量は記号を \(W\)、単位を \(\rm [J]\)(ジュール) あるいは \(\rm [Ws]\)(ワット秒)、\(\rm [kWh]\)(キロワット時) などで表します。
■ 電力量は、電力 × 時間 です
電力とは、単位時間(1秒間)当たりの電力量のことです。
電力と電力量の関係は
電力 \(P=\cfrac{電力量}{時間}\)
\(P=\cfrac{VIt}{t}=VI\) [W] になります。
つまり、直流回路の電力 \(P\) は、電圧 \(V\) と電流 \(I\) の積になります。
電力 \(P\) =電圧 \(V\) × 電流 \(I\) [W]
直流回路の電圧、電流、抵抗から電力と電力量を求める時
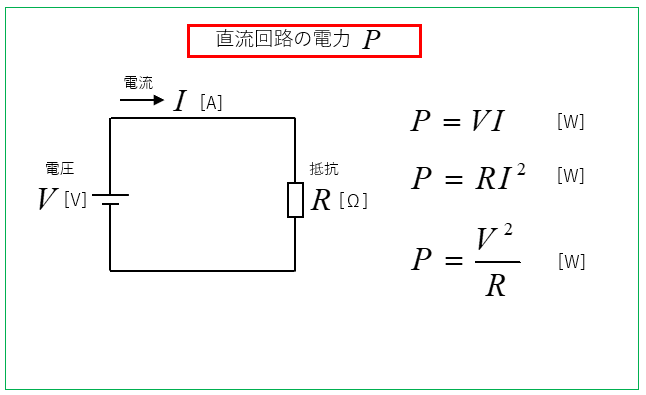
■ 電圧 \(V\) と電流 \(I\)から求める
電力 \(P=VI\) [W]
電力量 \(W=VIt\) [Ws] または \(\rm [J]\)
■ 抵抗 \(R\) と電流 \(I\) から求める
電力 \(P=RI^2\) [W]
電力量 \(W=RI^2t\) [Ws] または \(\rm [J]\)
■ 抵抗 \(R\) と電圧 \(V\) から求める
電力 \(P=\cfrac{V^2}{R}\) [W]
電力量 \(W=\cfrac{V^2}{R}t\) [Ws] または \(\rm [J]\)
練習問題
問題1
豆電球に直流電圧3ボルトを加えたら、2アンペアの電流が流れました。
豆電球を2時間、点灯したときの電力量はいくらになるか求めよ。
<解 答>
電力量は次の式で求められます。
\(W=VQ=VIt\) [J]
電力量の時間の単位は秒ですから、2時間を秒に換算すると、7200秒になります。
電力量= \(3ボルト×2アンペア×7200秒\)
電力量=\(43200\) [J](ジュール)
問題2
800Wの電熱器を30分使用しました。電力量を求めよ。
<解 答>
\(W=EIt=Pt=800×30×60=1.44×10^6 \) [J]
\(W=1.44×10^6×\cfrac{1}{3600×10^3}=0.4\) [kWh]
電力量は
\(0.4\) [kWh] になります。
問題3
1.2KWの電熱器を1日に2時間使用し、100Wの電球4個を5時間、70Wのテレビを6時間、40Wの冷蔵庫を24時間使用する過程における1ヶ月(30日)の使用電力量を求めよ。
<解 答>
\(W\)\(=(1200×2+100×4×5\)\(+70×6+40×24)×30\)
\(W=173400\hspace{8px}\rm Wh=173.4\) [kWh]
以上で「直流回路の電力と電力量」の説明を終わります。