Δ(デルタ)接続から、Y(スター)接続へ変換します。
ここでは、各相の負荷をインピーダンスでなく、抵抗を使って説明していきます。
Δ(デルタ)接続からY(スター)接続へ変換
Δ 接続回路をY 接続回路に変換するには
図1のΔ 接続回路と図2のY 接続回路の端子 A-B、B-C、C-Aの各端子間の合成抵抗が、それぞれ等しいとすることで求められます。

デルタ(Δ)からスター(Y)へ変換後の各抵抗値
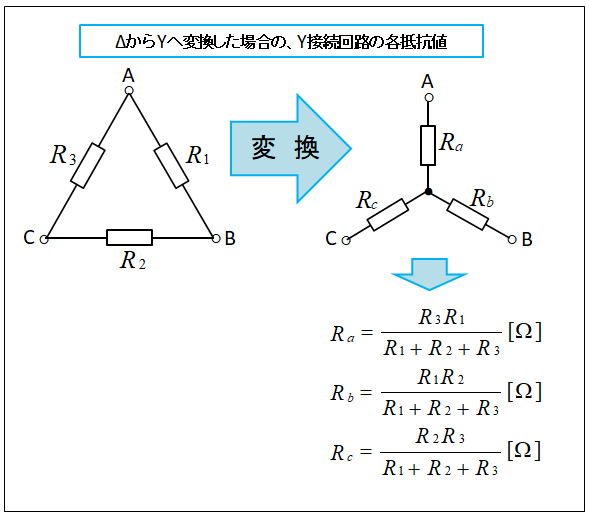
Δ から Y へ変換した場合の、Y 接続回路の各抵抗値は、次のようになります。
\(R_a=\cfrac{R_3R_1}{R_1+R_2+R_3}\) [Ω]
\(R_b=\cfrac{R_1R_2}{R_1+R_2+R_3}\) [Ω]
\(R_c=\cfrac{R_2R_3}{R_1+R_2+R_3}\) [Ω]
各相の抵抗値が等しい場合
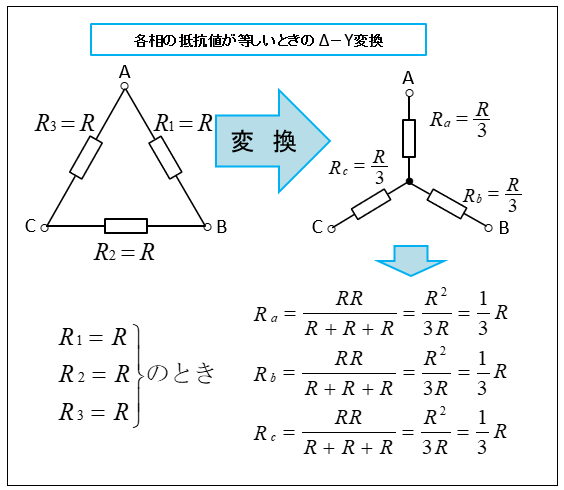
ここで、Δ 回路の抵抗 \(R_1、R_2、R_3\) の大きさが同じで \(R\) とすると、それぞれ \(\cfrac{1}{3}\) の大きさになります。
\(R_a=\cfrac{1}{3}R\) [Ω]
\(R_b=\cfrac{1}{3}R\) [Ω]
\(R_c=\cfrac{1}{3}R\) [Ω]
<証明>
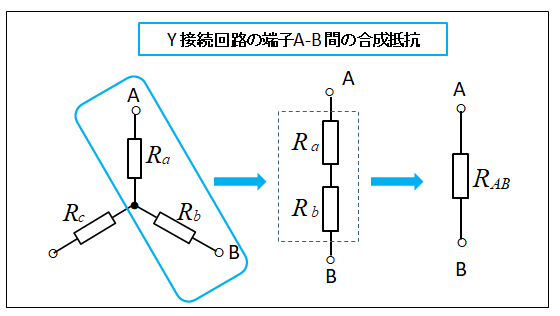
端子 A-B 間の合成抵抗を求めます
■ デルタ(Δ)回路の端子 A-B 間を計算します
端子 A-B 間から見た合成抵抗を \(R_{AB}\) として、合成抵抗値を求めます。
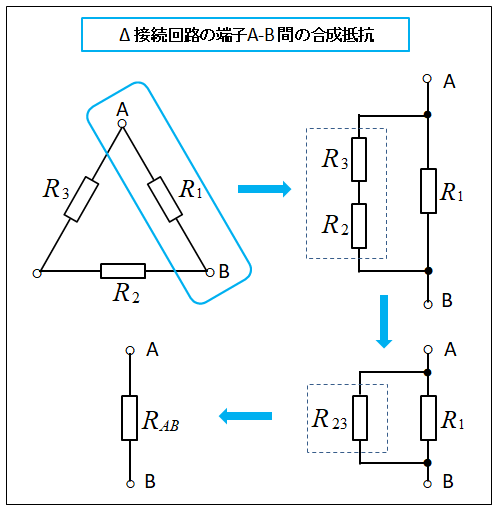
\(R_2\)と \(R_3\) は直列接続なので、この抵抗を \(R_{23}\) とします。
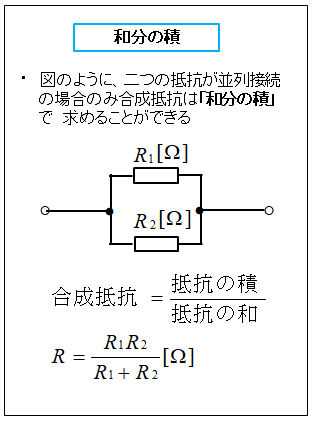
\(R_{AB}\)は \(R_1\) と \(R_{23}\) の並列接続なので、和分の積 で求められます。
\(R_{23}=R_2+R_3\)
\(R_{AB}=\cfrac{R_1R_{23}}{R_1+R_{23}}\)
\(R_{AB}=\cfrac{R_1(R_2+R_3)}{R_1+(R_2+R_3)}\)
\(R_{AB}=\cfrac{R_1R_2+R_3R_1}{R_1+R_2+R_3} \cdots(1)\)
■ スター(Y)回路の端子 A-B 間を計算します
Y 接続回路では A-B 間からみた合成抵抗は、\(R_a\) と \(R_b\) が直列接続ですから、その合成抵抗は、次のようになります。
\(R_{AB}=R_a+R_b \cdots(2)\)
■ Δ-Y 変換が等価であるためには、両回路の \(R_{AB}\) 式(1)と 式(2)が等しい
\(R_{AB}=\cfrac{R_1R_2+R_3R_1}{R_1+R_2+R_3} \cdots(1)\)
\(R_{AB}=R_a+R_b \cdots(2)\)
式(1)と式(2)が等しいとすると
\(R_a+R_b=\cfrac{R_1R_2+R_3R_1}{R_1+R_2+R_3} \cdots(3)\)
端子 B-C 間の合成抵抗を求めます
■ デルタ(Δ)回路の端子 B-C 間を計算します
同様にして、端子 B-C 間からみた合成抵抗 \(R_{BC}\) を求める。
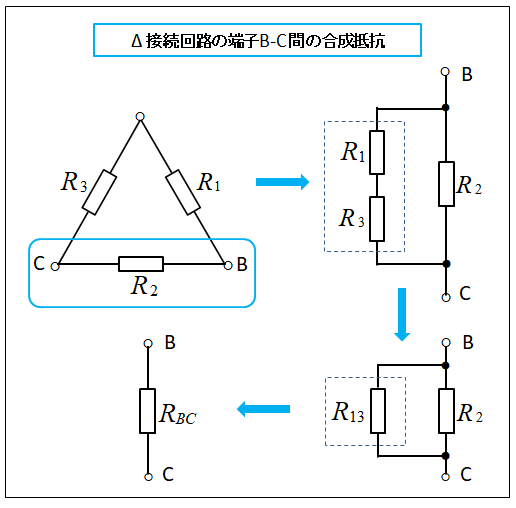
\(R_1\) と \(R_3\) は直列接続なので、合成抵抗を \(R_{13}=R_1+R_3\) とします。
\(R_{BC}\) は \(R_2\) と \(R_{13}\) の並列接続なので
\(R_{13}=R_1+R_3\)
\(R_{BC}=\cfrac{R_2R_{13}}{R_2+R_{13}}\)
\(R_{BC}=\cfrac{R_2(R_1+R_3)}{R_2+(R_1+R_3)}\)
\(R_{BC}=\cfrac{R_1R_2+R_2R_3}{R_1+R_2+R_3} \cdots(4)\)
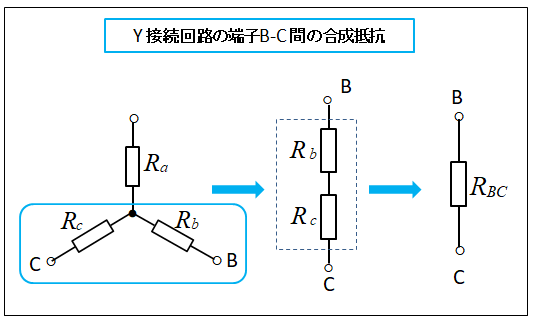
■ スター(Y)回路の端子 B-C 間を計算します
Y接続回路では B-C 間からみた合成抵抗は、\(R_b\) と \(R_c\) が直列接続ですから、その合成抵抗は次のようになります。
\(R_{BC}=R_b+R_c \cdots(5)\)
■ Δ-Y 変換が等価であるためには、両回路の \(R_{BC}\) 式(4)と 式(5)が等しい
\(R_{BC}=\cfrac{R_1R_2+R_2R_3}{R_1+R_2+R_3} \cdots(4)\)
\(R_{BC}=R_b+R_c \cdots(5)\)
式(4)と式(5)が等しいとすると
\(R_b+R_c=\cfrac{R_1R_2+R_2R_3}{R_1+R_2+R_3} \cdots(6)\)
端子 C-A 間の合成抵抗を求めます
■ デルタ(Δ)回路の端子 C-A 間を計算します
同様にして、端子 C-A 間からみた合成抵抗\(R_{CA}\) を求めます。
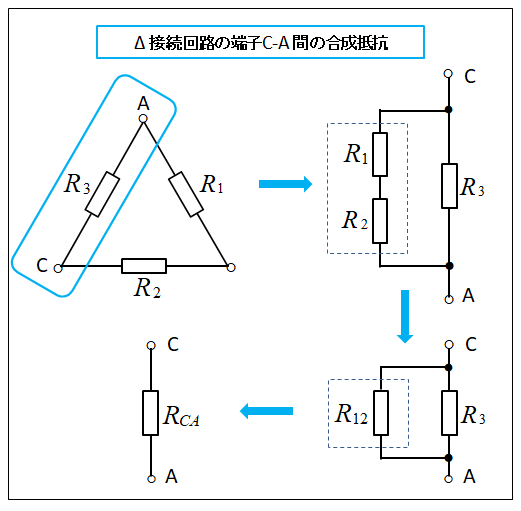
\(R_1\) と \(R_2\) は直列接続で合成抵抗を \(R_{12}=R_1+R_2\) とします。
\(R_{CA}\) は \(R_3\) と \(R_{12}\) の並列接続なので、
\(R_{12}=R_1+R_2\)
\(R_{CA}=\cfrac{R_3R_{12}}{R_3+R_{12}}\)
\(R_{CA}=\cfrac{R_3(R_1+R_2)}{R_3+(R_1+R_2)}\)
\(R_{CA}=\cfrac{R_3R_1+R_2R_3}{R_1+R_2+R_3} \cdots(7)\)
■ スター(Y)回路の端子 C-A 間を計算します
Y接続回路では C-A 間からみた合成抵抗は、\(R_cとR_a\) が直列接続ですから、その合成抵抗は次のようになります。
\(R_{CA}=R_c+R_a\tag{8}\)
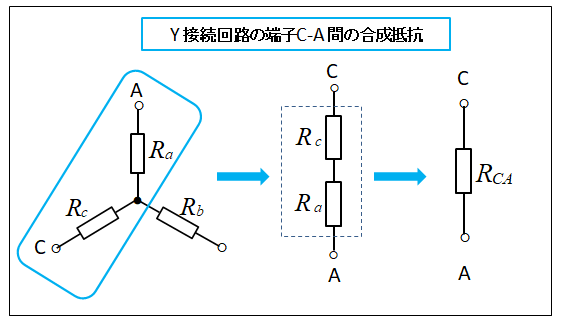
■ Δ-Y 変換が等価であるためには、両回路の \(R_{CA}\) 式(7) と 式(8)が等しくなければなりません。
\(R_{CA}=\cfrac{R_3R_1+R_2R_3}{R_1+R_2+R_3} \cdots(7)\)
\(R_{CA}=R_c+R_a \cdots(8)\)
式(7)と式(8)が等しいとすると
\(R_c+R_a\)\(=\cfrac{R_3R_1+R_2R_3}{R_1+R_2+R_3} \cdots(9)\)
\(R_a、R_b、R_c\) を求めます
上式の式(3)、式(6)、式(9)から
\(R_a+R_b=\cfrac{R_1R_2+R_3R_1}{R_1+R_2+R_3} \cdots(3)\)
\(R_b+R_c=\cfrac{R_1R_2+R_2R_3}{R_1+R_2+R_3} \cdots(6)\)
\(R_c+R_a=\cfrac{R_3R_1+R_2R_3}{R_1+R_2+R_3} \cdots(9)\)
式(3)、式(6)、式(9)の左辺と右辺をそれぞれ加算します。
\(2(R_a+R_b+R_c)\)\(=\cfrac{2(R_1R_2+R_2R_3+R_3R_1)}{R_1+R_2+R_3}\)
\(R_a+R_b+R_c\)\(=\cfrac{R_1R_2+R_2R_3+R_3R_1}{R_1+R_2+R_3}\)\(\cdots(10)\)
\(R_a\) を求めるには、式(10)から式(6)を引くと
\(R_a+R_b+R_c-(R_b+R_c)\)\(=\cfrac{R_1R_2+R_2R_3+R_3R_1}{R_1+R_2+R_3}\)\(-\cfrac{(R_1R_2+R_2R_3)}{R_1+R_2+R_3}\)
\(R_a=\cfrac{R_3R_1}{R_1+R_2+R_3} \cdots(11)\)
\(R_b\) を求めるには、式(10)から式(9)を引くと
\(R_a+R_b+R_c-(R_c+R_a)\)\(=\cfrac{R_1R_2+R_2R_3+R_3R_1}{R_1+R_2+R_3}\)\(-\cfrac{(R_3R_1+R_2R_3)}{R_1+R_2+R_3}\)
\(R_b=\cfrac{R_1R_2}{R_1+R_2+R_3}\)\(\cdots(12)\)
\(R_c\) を求めるには、式(10)から式(3)を引くと
\(R_a+R_b+R_c-(R_c+R_a)\)=\(\cfrac{R_1R_2+R_2R_3+R_3R_1}{R_1+R_2+R_3}-\cfrac{(R_1R_2+R_3R_1)}{R_1+R_2+R_3}\)
\(R_c=\cfrac{R_2R_3}{R_1+R_2+R_3}\)\(\cdots(13)\) となります。
以上のように、\(R_a、R_b、R_c\) の値を求めることができました。
練習問題
問題1
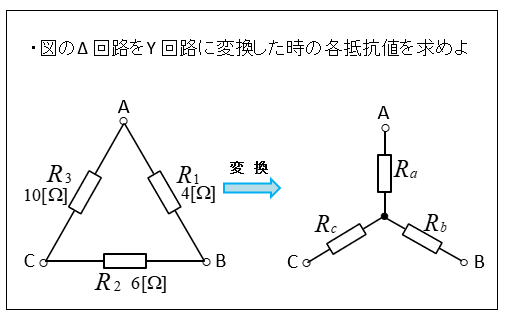
<解 答>
\(R_a=\cfrac{10×4}{4+6+10}=\cfrac{40}{20}=2\) [Ω]
\(R_b=\cfrac{4×6}{4+6+10}=\cfrac{24}{20}=1.2\) [Ω]
\(R_c=\cfrac{6×10}{4+6+10}=\cfrac{60}{20}=3\) [Ω]
問題2
次の回路に流れる電流 \(I\) [A] を求めよ。
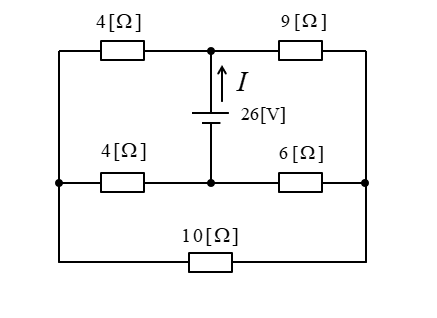
<解 答>
回路図を変形すると、下側の3つの抵抗がΔ(デルタ)接続になっています。
ここで、Δ-Y変換をすると図のようになります。
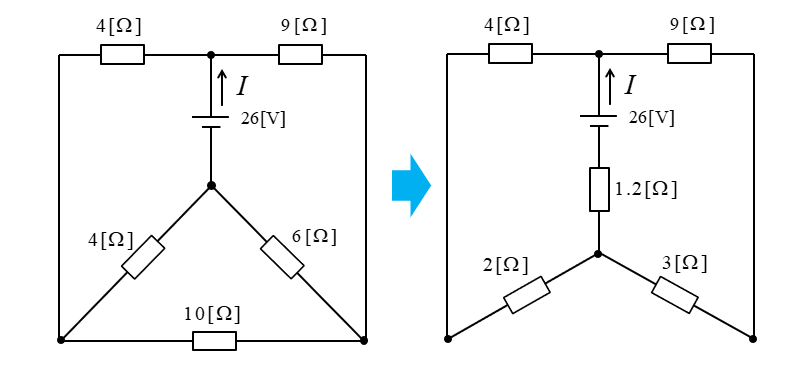
回路図を整理すると次のようになります。
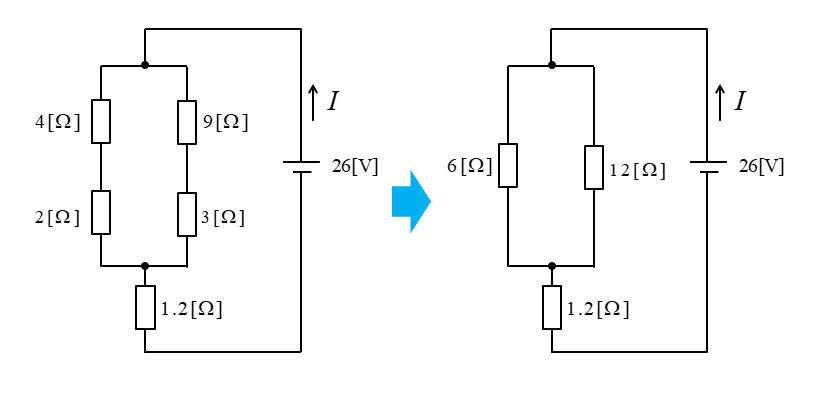
さらに整理すると、次のようになります。
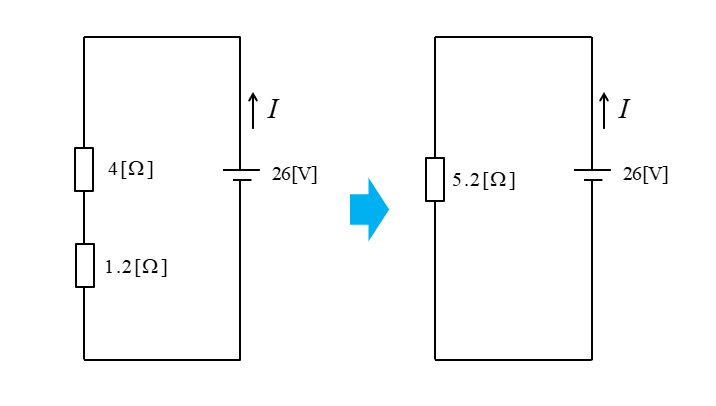
したがって
\(I=\cfrac{26}{5.2}=5\) [A] になります。
以上で「Δ-Y変換回路とは」の説明を終わります。