- この記事では、ブリッジ回路の意味を説明します。
- ブリッジ回路がどういう時に平衡するのか?
- ブリッジ回路は何の役に立つのか? について紹介します。

抵抗のブリッジ回路とは
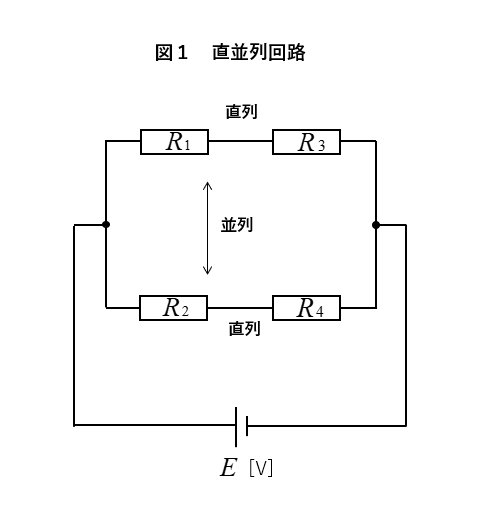
★ 図1は
抵抗 \(R_1\) と \(R_3\) 、抵抗 \(R_2\) と \(R_4\) を直列に接続し、直列接続した抵抗を並列に接続した 抵抗の直並列回路 です。
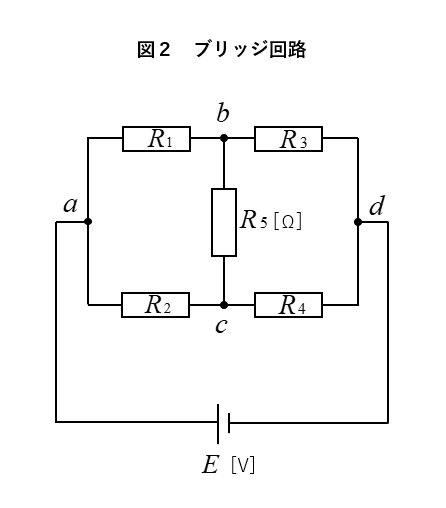
★ 図2のように
抵抗の直並列回路の \(b\) と \(c\) に、抵抗 \(R_5\) を接続します。
カタチが ブリッジ(橋)をかけたような形になるので
この回路を ブリッジ回路 といいます。
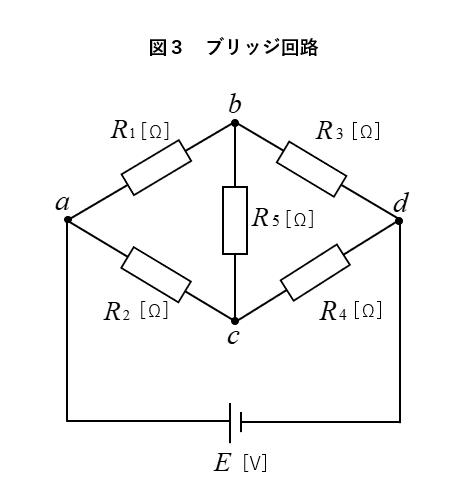
ブリッジ回路の平衡条件
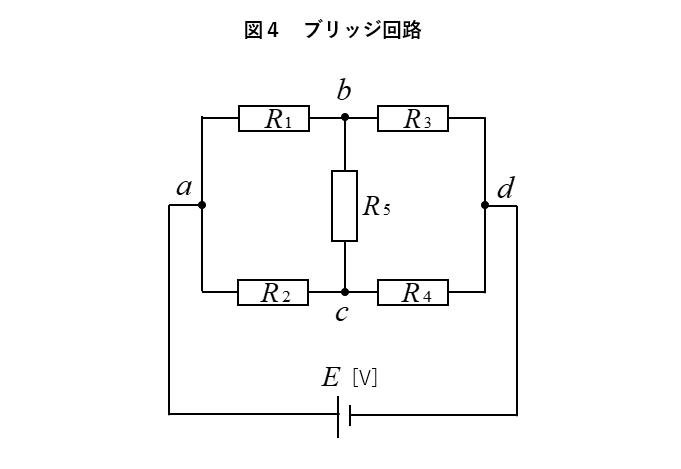
★ 図4のブリッジ回路で
抵抗 \(R_1、R_2、R_3、R_4\) の値が
\(\cfrac{R_1}{R_2}=\cfrac{R_3}{R_4}\) の関係になると
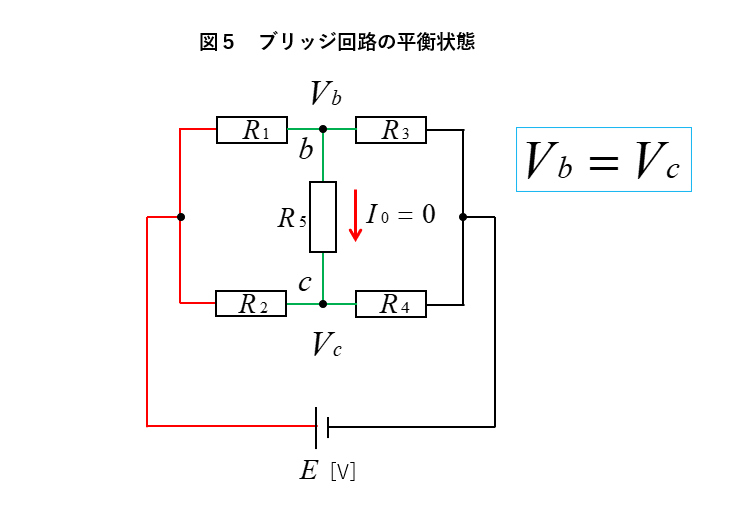
★ 図5のように
\(V_b\) と \(V_c\) の電位が等しくなり
\(R_5\) の抵抗に 電流 \(I_0\) が流れない状態になります。
この状態を ブリッジ回路の平衡状態 といいます。
\(\cfrac{R_1}{R_2}=\cfrac{R_3}{R_4}\)
式を変形すると
\(R_1R_4=R_2R_3\)
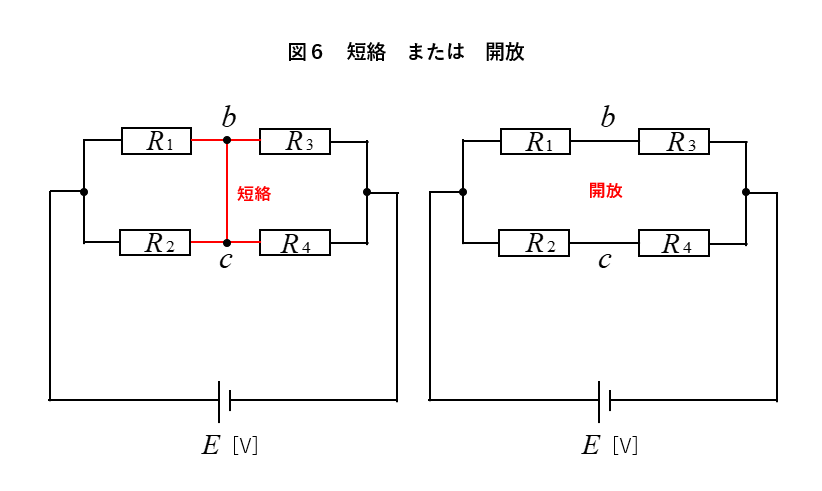
ブリッジ回路が平衡したときは
図6のように \(b\) と \(c\) を
短絡または開放 して
回路を簡単にすることができます。
ブリッジ回路の平衡状態
★ 図7のように
ブリッジ回路の上側と下側の抵抗値が
\(\cfrac{R_1}{R_2}=\cfrac{R_3}{R_4}\) の関係になると
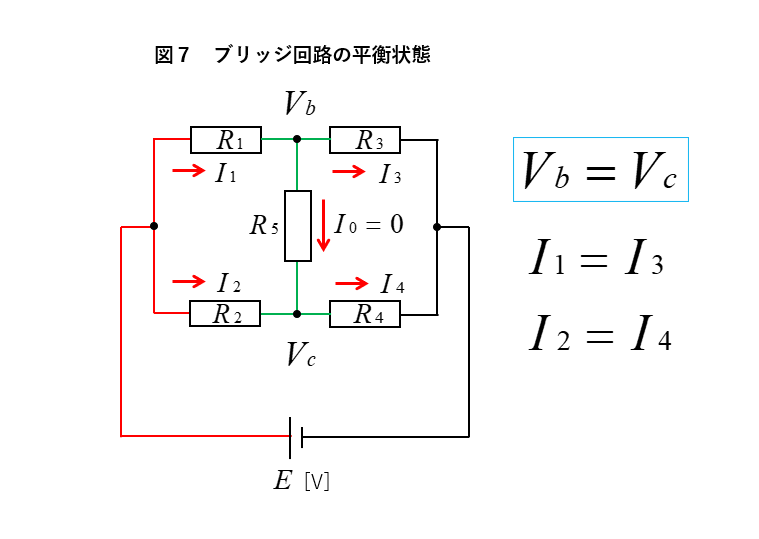
\(R_1I_1\) と \(R_2I_2\) の電圧降下が、等しくなります。
したがって、\(V_b\) と \(V_c\) の 電位 は同じになります。
ブリッジ抵抗 \(R_5\) には、電流が流れません。
\(I_0=0\) なので
\(I_1=I_3\) 、\(I_2=I_4\) になります。
ブリッジ抵抗 \(R_5\) に、電流が流れない状態のことを
ブリッジが平衡している状態 といいます。
ブリッジ回路が平衡したときの電圧
★ ブリッジ回路が平衡しているときは
\(b\) と \(c\) の電位が同じなので
図8のように開放(または短絡)することができます。
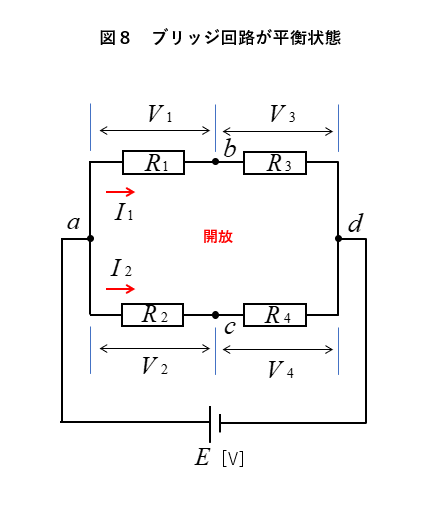
次の式が成立します。
\(V_1=V_2\)
オームの法則から
\(R_1I_1=R_2I_2 \cdots (1)\)
同じように
\(V_3=V_4\)
オームの法則から
\(R_3I_1=R_4I_2 \cdots (2)\)
式(1)を 式(2)で割ります。
\(\cfrac{R_1}{R_3}=\cfrac{R_2}{R_4} \cdots (3)\)
式(3)を変形すると
\(R_1R_4=R_2R_3\)
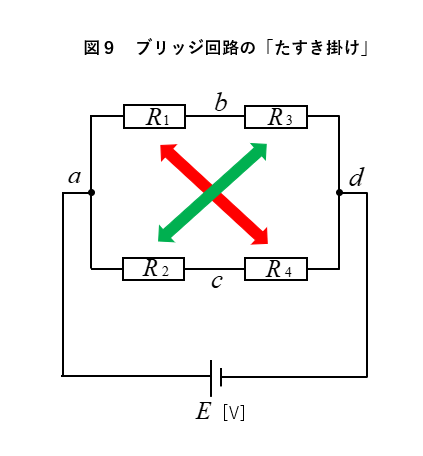
ブリッジ回路が平衡する時は、図9のように
抵抗の たすき掛け になるので
「たすき掛け」といわれます。
★ 式(3)を変形して、次のようにすると
\(\cfrac{R_1}{R_2}=\cfrac{R_3}{R_4} \cdots (4)\)
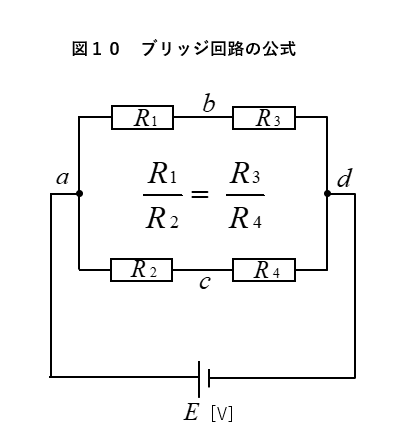
図10のように、上側の抵抗を
下側の抵抗で割った形になります。
例題
★ 図のブリッジ回路が平衡している時
\(R_3\) の抵抗値を求めよ。
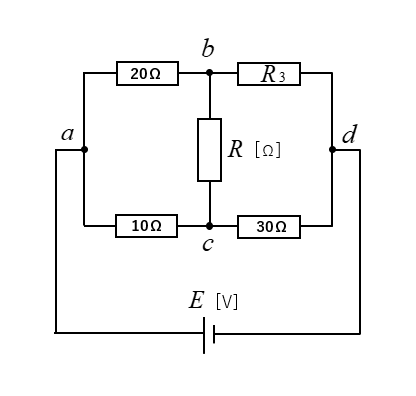
<解答例>
ブリッジ回路の平衡の公式から
\(\cfrac{R_1}{R_2}=\cfrac{R_3}{R_4}\)
\(\cfrac{20}{10}=\cfrac{R_3}{30}\)
\(R_3=60\) [Ω] になります。
まとめ
ブリッジ回路の特徴
ブリッジ回路が平衡した時には、ブリッジ抵抗に電流が流れない状態 になります。
平衡した時には「4つの抵抗」のうち、3つの抵抗値 がわかれば、残りの抵抗値を正確に知ることができます。
\(\cfrac{R_1}{R_2}=\cfrac{R_3}{R_4}\)
式を変形すると
\(R_1R_4=R_2R_3\)
以上で「ブリッジ回路とは」の説明を終わります。