Y(スター)接続からΔ(デルタ)接続への変換について説明します。
ここでは、各相の負荷をインピーダンスでなく、抵抗を使って説明していきます。
Y 結線からΔ 結線接続へ変換
Y 接続回路をΔ 接続回路に変換するには
図1のY 接続回路と図2のΔ 接続回路の端子A-B、B-C、C-Aの各端子間の合成抵抗は、それぞれ等しいとすることで求められます。
Y 結線からΔ 結線へ変換後の各抵抗値
Y からΔ へ変換した場合の、Δ 接続回路の各抵抗値は、次のようになります。
\(R_1\)\(=\cfrac{R_aR_b+R_bR_c+R_cR_a}{R_c}\) [Ω]
\(R_2\)\(=\cfrac{R_aR_b+R_bR_c+R_cR_a}{R_a}\) [Ω]
\(R_3\)\(=\cfrac{R_aR_b+R_bR_c+R_cR_a}{R_b}\) [Ω]

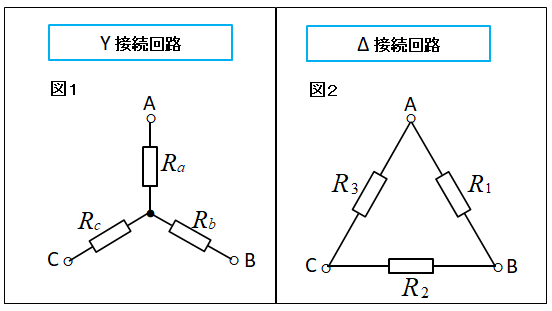
各相の抵抗値が等しい場合
ここで、Y 回路の抵抗 \(R_a、R_b、R_c\) の大きさが同じで \(R\) とすると、それぞれ 3倍の大きさになります。
\(R_1=3R\) [Ω]
\(R_2=3R\) [Ω]
\(R_3=3R\) [Ω]
<証明>
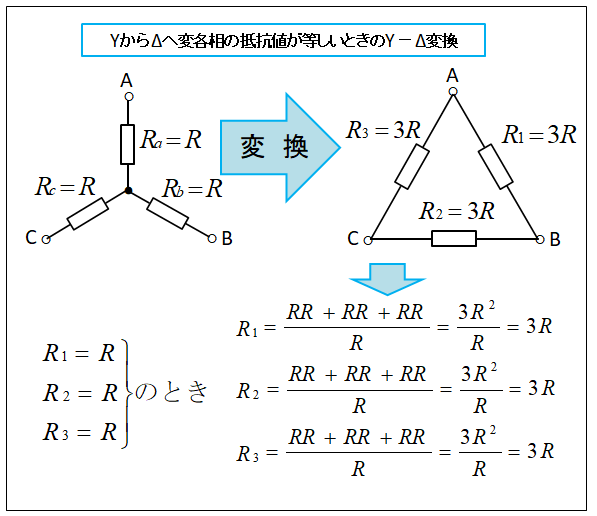
三つの抵抗 \(R_a、R_b、R_c\) が Y に接続された回路と、これと等価な Δ に接続された回路に変換した各抵抗 \(R_1、R_2、R_3\) を求めます。
端 子A-D 間の合成抵抗を求めます
■ スター(Y)回路の端子 A-D 間を計算します
端子 B-C 間を短絡し、この端子を D とします。
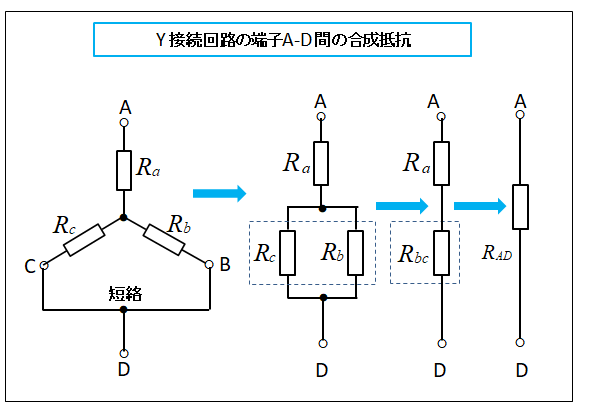
図の端子 A-D 間の抵抗は、抵抗 \(R_b、R_c\) の並列接続に抵抗 \(R_a\) が直列に接続された直並列回路になります。
抵抗 \(R_b、R_c\) の並列回路の合成抵抗 \(R_{bc}\) は、「和分の積」から
\(R_{bc}=\cfrac{R_bR_c}{R_b+R_c}\)
従って、端子 A-D 間の合成抵抗 \(R_{AD}\) は
\(R_{AD}=R_a+R_{bc}\)\(=R_a+\cfrac{R_bR_c}{R_b+R_c}\)
\(R_{AD}=\cfrac{R_aR_b+R_bR_c+R_cR_a}{R_b+R_c}\)
\(R_{AD}\) の逆数をとると、次のようになります。
\(\cfrac{1}{R_{AD}}=\cfrac{R_b+R_c}{R_aR_b+R_bR_c+R_cR_a}\cdots(1)\)
■ デルタ(Δ)回路の端子 A-D 間を計算します
次に、Δ 接続回路で端子 B-C 間を短絡し、この端子を D とします。
端子 A と端子 D から見た合成抵抗 \(R_{AD}\) は抵抗 \(R_1\) と \(R_3\) の並列接続になります。
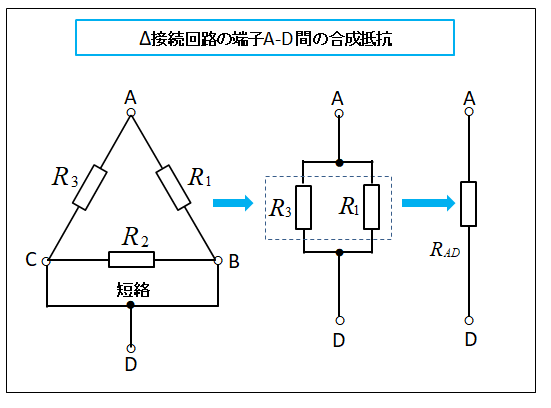
合成抵抗 \(R_{AD}\) の逆数をとると、次のようになります。
\(\cfrac{1}{R_{AD}}\)\(=\cfrac{1}{R_1}+\cfrac{1}{R_3}\cdots(2)\)
■ Y-Δ 変換が等価であるためには、両回路の式(1)と式(2)が等しい
\(\cfrac{1}{R_{AD}}=\cfrac{R_b+R_c}{R_aR_b+R_bR_c+R_cR_a}\cdots(1)\)
\(\cfrac{1}{R_{AD}}=\cfrac{1}{R_1}+\cfrac{1}{R_3}\cdots(2)\)
式(1)と式(2)が等しいとすると
\(\cfrac{1}{R_1}+\cfrac{1}{R_3}=\cfrac{R_b+R_c}{R_aR_b+R_bR_c+R_cR_a}\cdots(3)\)
端子 B-E 間 の合成抵抗を求めます
■ スター(Y)回路の端子 B-E 間 を計算します
端子 C-A 間 を短絡し、この端子を E とします。
同じように、端子 B-E 間 の合成抵抗 \(R_{BE}\) は次のようになります。
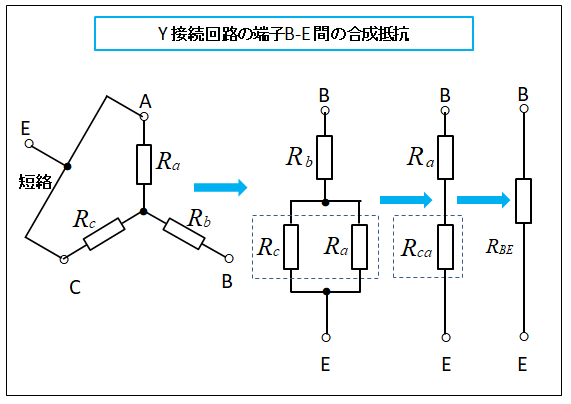
抵抗 \(R_c、R_a\) の並列回路の合成抵抗 \(R_{ca}\) は
\(R_{ca}=\cfrac{R_cR_a}{R_c+R_a}\)
従って、端子 B-E 間 の合成抵抗 \(R_{BE}\) は
\(R_{BE}=R_b+R_{ca}=R_b+\cfrac{R_cR_a}{R_c+R_a}\)
\(R_{BE}=\cfrac{R_aR_b+R_bR_c+R_cR_a}{R_c+R_a}\)
\(R_{BE}\) の逆数をとると、次のようになります。
\(\cfrac{1}{R_{BE}}=\cfrac{R_c+R_a}{R_aR_b+R_bR_c+R_cR_a}\cdots(4)\)
■ デルタ(Δ)回路の端子 B-E 間 を計算します
端子 C-A 間 を短絡し、この端子を E とします。
端子 E と端子 B から見た合成抵抗 \(R_{BE}\) は、抵抗 \(R_1\) と \(R_2\) の並列接続になります。
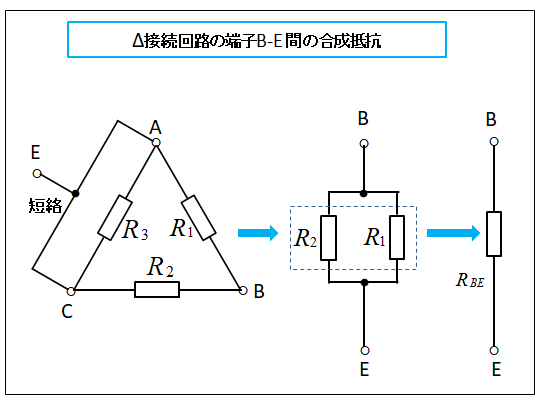
合成抵抗 \(R_{BE}\) の逆数をとると、次のようになります。
\(\cfrac{1}{R_{BE}}=\cfrac{1}{R_1}+\cfrac{1}{R_2} \cdots(5)\)
■ Y-Δ 変換が等価であるためには、両回路の式(4)と式(5)が等しい
\(\cfrac{1}{R_{BE}}=\cfrac{R_c+R_a}{R_aR_b+R_bR_c+R_cR_a}\cdots(4)\)
\(\cfrac{1}{R_{BE}}=\cfrac{1}{R_1}+\cfrac{1}{R_2}\cdots(5)\)
式(4)と式(5)が等しいとすると
\(\cfrac{1}{R_1}+\cfrac{1}{R_2}=\cfrac{R_c+R_a}{R_aR_b+R_bR_c+R_cR_a}\cdots(6)\)
端子 C-F 間 の合成抵抗を求めます
■ スター(Y)回路の端子 C-F 間 を計算します
端子 A-B 間 を短絡し、この端子を F とします。
同じように、端子 C-F 間 の合成抵抗 \(R_{CF}\) は次のようになります。
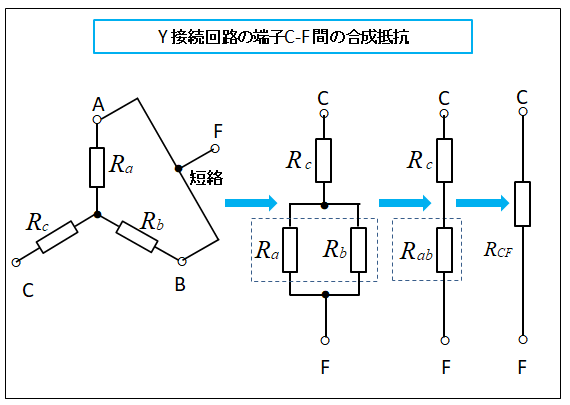
抵抗 \(R_a、R_b\) の並列回路の合成抵抗 \(R_{ab}\) は
\(R_{ab}=\cfrac{R_aR_b}{R_a+R_b}\)
従って、端子 C-F 間 の合成抵抗 \(R_{CF}\) は
\(R_{CF}=R_c+R_{ab}=R_c+\cfrac{R_aR_b}{R_a+R_b}\)
\(R_{CF}=\cfrac{R_aR_b+R_bR_c+R_cR_a}{R_a+R_b}\)
\(R_{CF}\) の逆数をとると、次のようになります。
\(\cfrac{1}{R_{CF}}=\cfrac{R_a+R_b}{R_aR_b+R_bR_c+R_cR_a}\cdots(7)\)
■ デルタ(Δ)回路の端子 C-F 間 を計算します
端子 A-B 間 を短絡し、この端子を F とします。
端子 C と 端子 F から見た、合成抵抗 \(R_{CF}\) は抵抗 \(R_2\) と \(R_3\) の並列接続です。
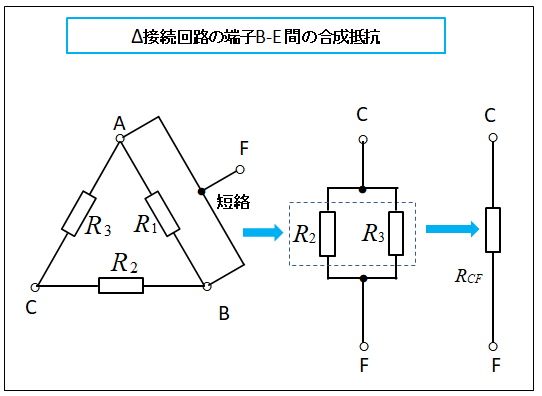
合成抵抗 \(R_{CF}\) の逆数をとると、次のようになります。
\(\cfrac{1}{R_{CF}}=\cfrac{1}{R_2}+\cfrac{1}{R_3}\cdots(8)\)
■ Y-Δ 変換が等価であるためには、両回路の式(7)と式(8)が等しい
\(\cfrac{1}{R_{CF}}=\cfrac{R_a+R_b}{R_aR_b+R_bR_c+R_cR_a}\cdots(7)\)
\(\cfrac{1}{R_{CF}}=\cfrac{1}{R_2}+\cfrac{1}{R_3}\cdots(8)\)
式(7)と式(8)が等しいとすると
\(\cfrac{1}{R_2}+\cfrac{1}{R_3}=\cfrac{R_a+R_b}{R_aR_b+R_bR_c+R_cR_a}\cdots(9)\)
R1、R2、R3 を求めます
上式の式(3)、式(6)、式(9)から
\(\cfrac{1}{R_1}+\cfrac{1}{R_3}=\cfrac{R_b+R_c}{R_aR_b+R_bR_c+R_cR_a}\cdots(3)\)
\(\cfrac{1}{R_1}+\cfrac{1}{R_2}=\cfrac{R_c+R_a}{R_aR_b+R_bR_c+R_cR_a}\cdots(6)\)
\(\cfrac{1}{R_2}+\cfrac{1}{R_3}=\cfrac{R_a+R_b}{R_aR_b+R_bR_c+R_cR_a}\cdots(9)\)
式(3)、式(6)、式(9)の左辺と右辺をそれぞれ加算します。
\(2\left(\cfrac{1}{R_1}+\cfrac{1}{R_2}+\cfrac{1}{R_3}\right)\)
\(=\cfrac{2(R_a+R_b+R_c)}{R_aR_b+R_bR_c+R_cR_a}\cdots(10)\)
式(10)の両辺を2で割ると
\(\cfrac{1}{R_1}+\cfrac{1}{R_2}+\cfrac{1}{R_3}\)
\(=\cfrac{R_a+R_b+R_c}{R_aR_b+R_bR_c+R_cR_a}\cdots(11)\)
\(R_1\) を求めるには、式(11)の右辺と左辺から、式(9)の右辺と左辺を引きます。
\(\cfrac{1}{R_1}+\cfrac{1}{R_2}+\cfrac{1}{R_3}-(\cfrac{1}{R_2}+\cfrac{1}{R_3})\)
\(=\cfrac{R_a+R_b+R_c}{R_aR_b+R_bR_c+R_cR_a}-\cfrac{R_a+R_b}{R_aR_b+R_bR_c+R_cR_a}\)
\(\cfrac{1}{R_1}=\cfrac{R_c}{R_aR_b+R_bR_c+R_cR_a}\cdots(12)\)
両辺の逆数をとると
\(R_1=\cfrac{R_aR_b+R_bR_c+R_cR_a}{R_c}\cdots(13)\)
★ \(R_2\) を求めるには、式(11)の右辺と左辺から式(3)の右辺と左辺を引いて、同様に計算すると
\(R_2=\cfrac{R_aR_b+R_bR_c+R_cR_a}{R_a}\cdots(14)\)
★ \(R_3\) を求めるには、式(11)の右辺と左辺から式(6)の右辺と左辺を引いて、同様に計算すると
\(R_3=\cfrac{R_aR_b+R_bR_c+R_cR_a}{R_b}\cdots(15)\)
以上のように、\(R_1、R_2、R_3\) が求めることができました。
練習問題
問題1
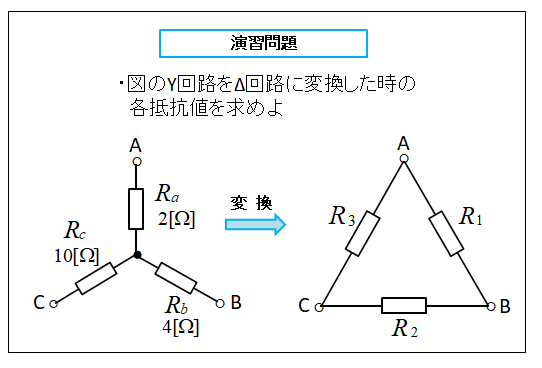
<解 答>
\(R_1=\cfrac{2×4+4×10+10×2}{10}\)\(=\cfrac{68}{10}=6.8\) [Ω]
\(R_2=\cfrac{2×4+4×10+10×2}{2}\)\(=\cfrac{68}{2}=34\) [Ω]
\(R_3=\cfrac{2×4+4×10+10×2}{4}\)\(=\cfrac{68}{4}=17\) [Ω]
以上で「Y-Δ変換回路とは」の説明を終わります。