ここではコンデンサの基本式の導き方とコンデンサが持つ特徴や役割について説明します。
電荷から出る電気力線の公式から、コンデンサの計算に必要な基本式を導いて行きます。
コンデンサの基本式
コンデンサ内部の電気力線
電荷 \(Q\) からは ガウスの法則 により、\(4πkQ\) [本] の 電気力線 が出ます。
1.図のように \(Q\) [C] の電荷を持つコンデンサがあります。
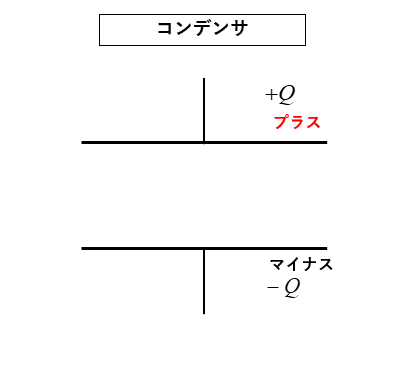
2.図のように \(+Q\) の極板からは、上下に \(2πkQ\) [本] の電気力線が出ています。
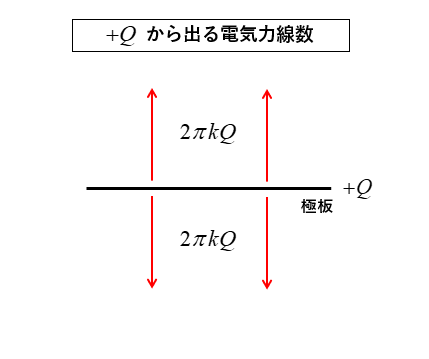
3.図のように \(-Q\) の極板からは、上下に \(2πkQ\) [本] の電気力線が出ています。
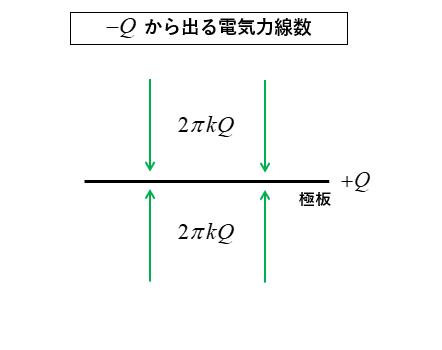
4.図のように コンデンサは2つの極板が向かい合っていますので、上下の電気力線は打ち消し合うのでゼロになります。
結果的にコンデンサの内部に \(4πkQ\) [本] の電気力線が発生します。
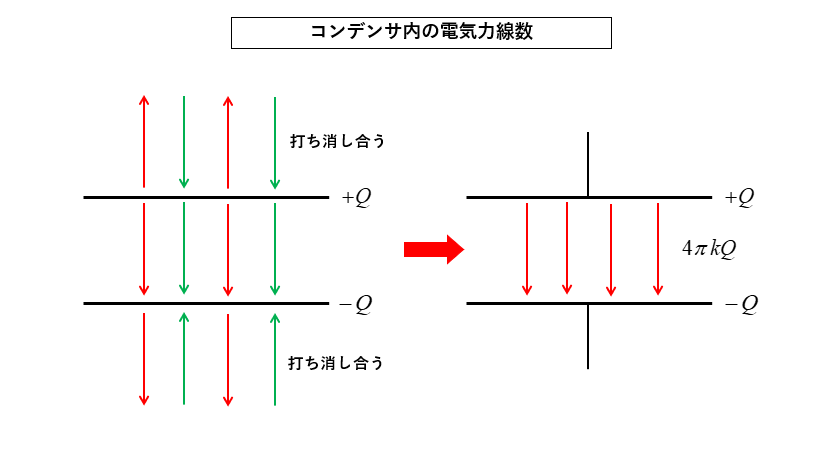
コンデンサの基本式
コンデンサの極板の面積を \(S\) [m2]
コンデンサの極板間隔を \(d\) [m]
コンデンサの電位差を \(V\) [V] とします。
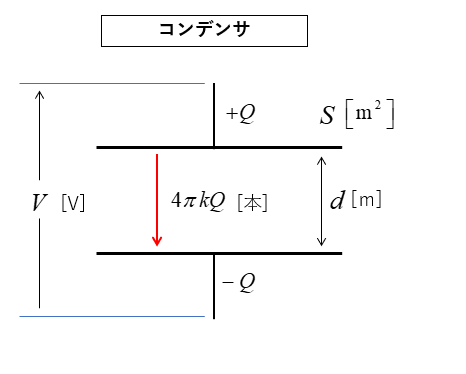
電気力線数 \(4πkQ\) [本] を
極板の面積 \(S\) で割ると
電界の強さ \(E\) になります。
\(E=\cfrac{4πkQ}{S}\cdots(1)\)
コンデンサの内部は、電界の強さが一様な電界ですから
電位差 \(V\) は
\(V=Ed\cdots(2)\)
式(2)に式(1)を代入します。
\(V=Ed=\cfrac{4πkQ}{S}×d\cdots(3)\)
式(3)を変形して
\(Q=\cfrac{1}{4πk}×\cfrac{S}{d}V\cdots(4)\)
誘電率の公式から
\(ε=\cfrac{1}{4πk}\cdots(5)\) ですから
式(4)は
\(Q=ε\cfrac{S}{d}V\cdots(6)\)
静電容量 \(C\) [F] は
\(C=ε\cfrac{S}{d}\) ですから
式(6)は
\(Q=CV\) [C] になります。
コンデンサの基本式
\(Q=CV\) [C]
\(C=ε\cfrac{S}{d}\) [F]
コンデンサの特徴
静電容量とは、コンデンサがどれだけの電荷の量を蓄えることができるかを表します。
キャパシタンスは静電容量の別の呼び方で、「静電容量=キャパシタンス」で同じことをいいます。
同じような用語として、「キャパシタ」というものがあります。
■ コンデンサ
一般的に、電子部品などの呼び名として「コンデンサ」を使いますが、同じようにコンデンサのことを「キャパシタ」と呼ぶこともあります。
コンデンサ=キャパシタで、電子部品の呼び方です。
コンデンサという呼び名は、電子部品だけでなく広く使われています。
エアコンの場合は熱交換器の凝縮器のことを コンデンサ と呼びます。
コンデンサは電極間に電気を蓄える性質がありますから
この性質を利用して音を電気の信号に変換することで コンデンサマイク として利用されています。
コンデンサの静電容量は 記号に \(C\) を使い、単位として [F] ファラド を使います。
■ 静電容量の単位
静電容量 \(C\) の単位は [F] ファラドを使います。
ファラドは非常に大きいので実際には、次のような大きさを使います。
- \(1×10^{-6}\) [μF] \(\cdots\)マイクロファラド
- \(1×10^{-9}\) [nF] \(\cdots\)ナノファラド
- \(1×10^{-12}\) [pF] \(\cdots\)ピコファラド
コンデンサと電荷の関係
■ コンデンサに電荷が無い時
図はコンデンサに電荷が貯まっていない様子を表しています。
コンデンサが充電されていないときは、電荷が無いと思ってしまいますよね。
実際は正電荷と負電荷が打ち消し合っている状態なので、電荷が無いように見えるわけです。
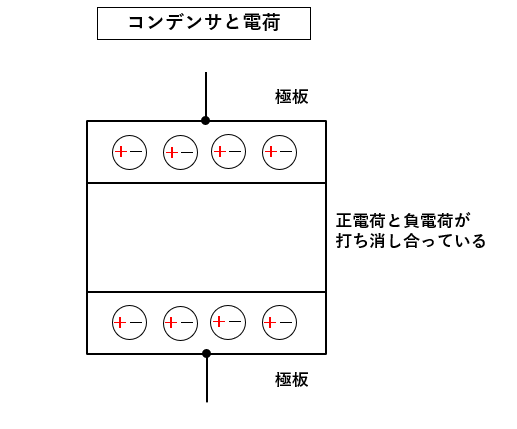
■ コンデンサに直流電圧を加えた時
コンデンサに直流電圧を加えると
図のように 正極 にある 自由電子 が電池の電圧により 負極 に移動します。
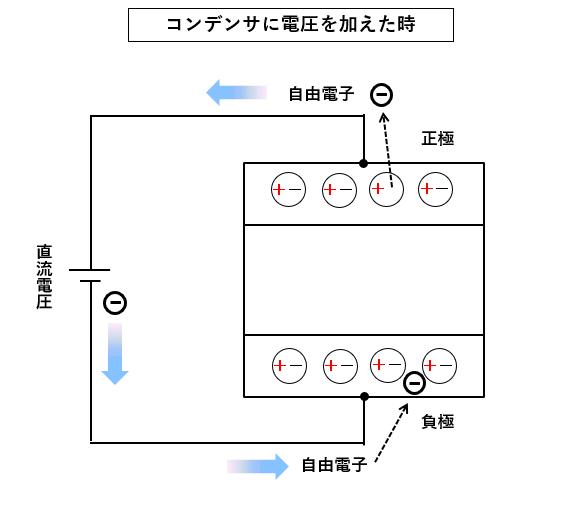
■ コンデンサの電圧が十分経過した時
コンデンサに電荷が十分充電されると、図のように負極に自由電子が貯まります。
正極にはプラスの電荷が多くなり、負極には電子が多くなるのでマイナスになります。
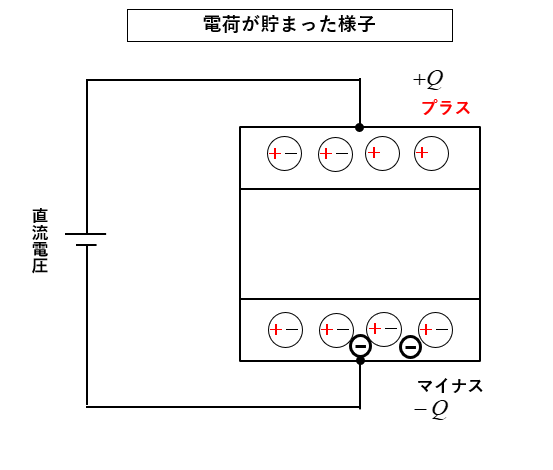
■ コンデンサの書き方
一般的に、図のように簡素化して表示します。
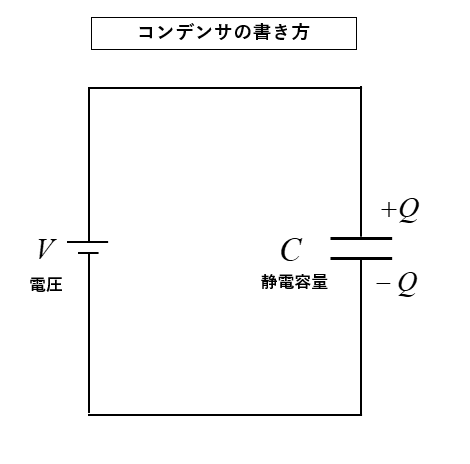
\(V\) [V]\(\cdots\)加える電圧
\(C\) [F]\(\cdots\)コンデンサの静電容量
\(Q\) [C]\(\cdots\)電荷量 とすると、次の関係式になります。
\(Q=CV\) [C]
■ 静電容量の単位
静電容量 \(C\) の単位は [F] ファラドを使います。
ファラドは非常に大きいので実際には、次のような大きさを使います。
- \(1×10^{-6}\) [μF] \(\cdots\)マイクロファラド
- \(1×10^{-9}\) [nF] \(\cdots\)ナノファラド
- \(1×10^{-12}\) [pF] \(\cdots\)ピコファラド
★ コンデンサは直列や並列に接続して使用することができます。
コンデンサを直列や並列に接続したときの静電容量は コンデンサの容量計算 として求めることができます。
コンデンサと電圧
コンデンサに直流電圧を加える時
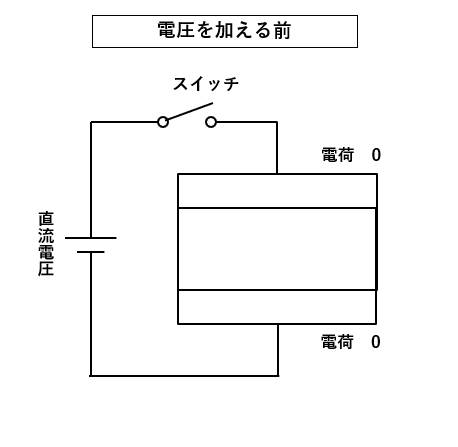
2.電圧を加えた直後では、電流 \(I\) が流れ始めます。
まだ、コンデンサに電荷は貯まっていません。
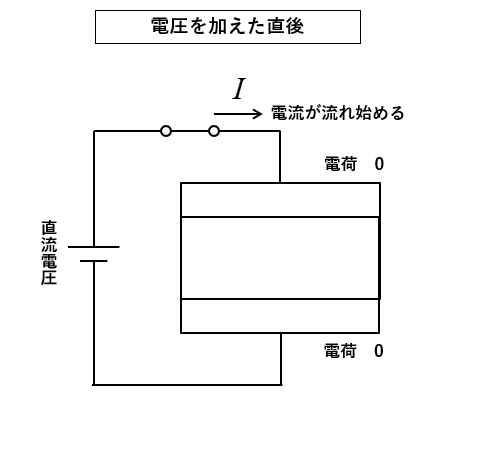
3.電圧を加えた途中では、電荷 \(q\) が貯まり始めます。
電流 \(ΔI\) は流れが小さくなって行きます。
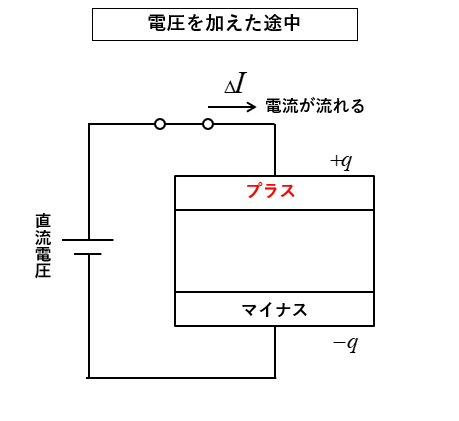
4.電圧を加えて時間が十分経過後になると、電荷 \(Q\) が貯まります。電流は流れなくなります。
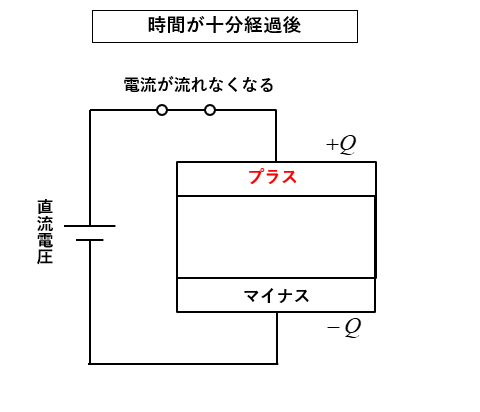
コンデンサの極板には、極性が反対で同じ量の電荷量が貯まります。
プラスが \(+Q\) クーロンなら、マイナスには \(-Q\) クーロンが貯まります。
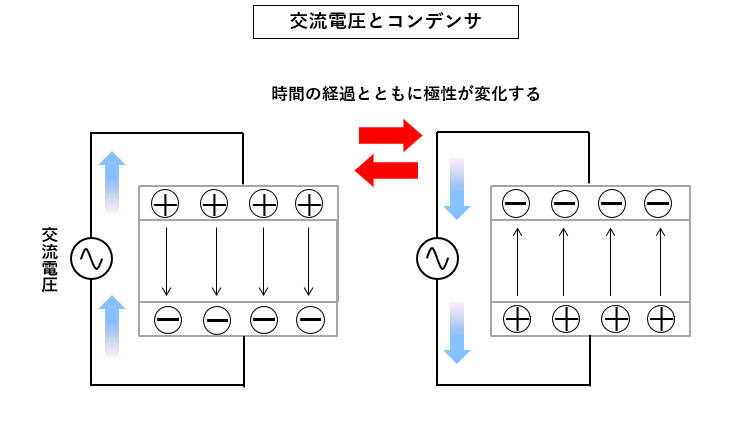
コンデンサに交流電圧を加える時
- コンデンサに交流をつなぐと、電流の向きが交互に変わるので充電と放電を繰り返すことになります。
- コンデンサの電極に貯まる電気も、それに応じて交互に変わります。
- この状態は、コンデンサに交流が流れているように見えます。
- この電流のことを 変位電流 と言います。
コンデンサの直流回路での役割り
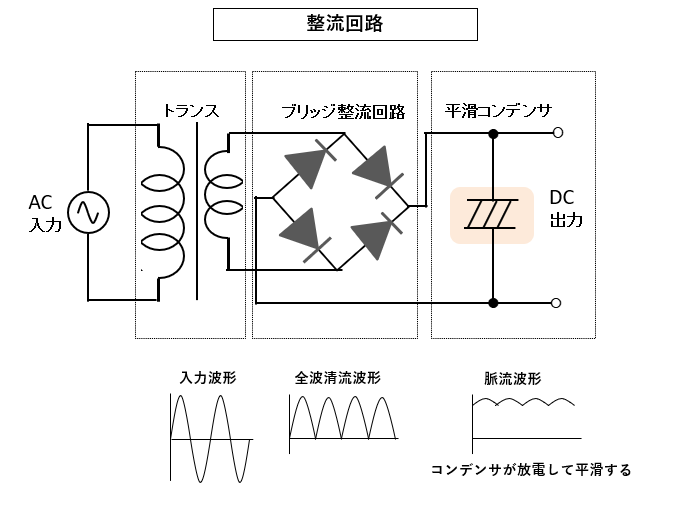
■ 整流回路の平滑コンデンサとしての役割り
図7のような整流回路において
コンデンサの役割りは交流を整流して直流を得る時に
脈流を平均して平らにするための 平滑コンデンサ としての役割りがあります。
この時に使われるのは、主にアルミ電解コンデンサが使われます。
アルミ電解コンデンサは、容量が大きく、プラスマイナスの極性があり、使用できる電圧が決まっています。
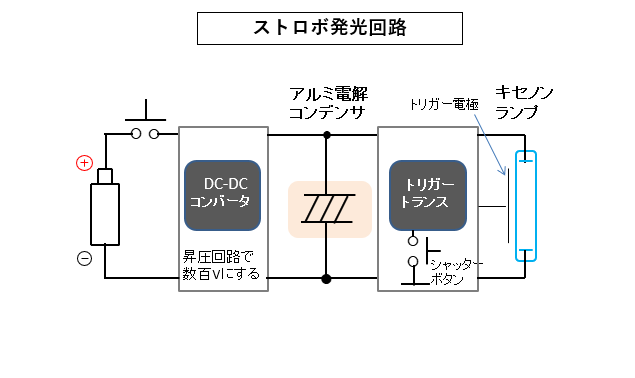
■ コンデンサ充放電を利用したストロボ発光回路
コンデンサに高圧の電気を充電して、コンデンサに蓄えられた電気を放出すればストロボを発光させることができます。
- 乾電池の電圧は数ボルトですから、昇圧回路で数百ボルトにします。
- 昇圧した電気を大容量の電解コンデンサに貯えます。
- トリガートランスでさらに昇圧して、キセノンランプを発光させます。
- 発光が終わると、再びコンデンサに充電させる仕組みです。
コンデンサの交流回路での役割り
■ コンデンサは交流回路では電気を通しますが 交流回路で抵抗 のような働きをします。
このことを 容量性リアクタンス といいます。
■ 容量性リアクタンスのことを \(X_C\) と書いて
\(X_C=\cfrac{1}{2πfC}\) [Ω] で表わします。
この式から分かるように、周波数の大きさに反比例しますので、周波数が高い交流ほど通しやすくなります。
コンデンサの周波数が高い交流ほどよく通るという性質を利用して、ある周波数の信号だけを通過させたりすることができます。
このことを同調と言いますが、ラジオやテレビなどがチャンネルで映るのはこの同調を利用して特定の電波を捉えているからです。
コンデンサの直流を通さずに交流だけを通すという機能を利用して、それぞれの電子回路の信号に合わせています。
このために使われているのが、カップリングコンデンサです。
また交流の信号の中のノイズを、アース側に逃がすという役目もあります。
このように交流回路において、コンデンサの役割りはたくさんあります。
練習問題
問題1
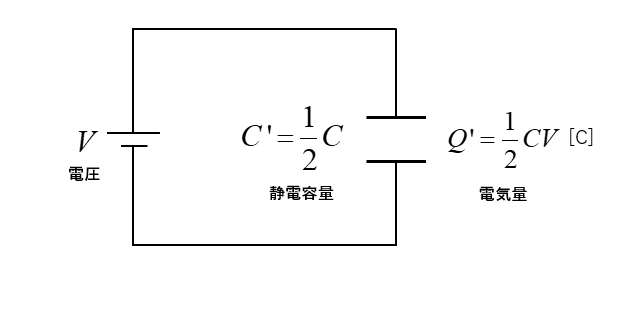
図のようなコンデンサ回路があります。
電池を接続したままで、コンデンサの極板間隔を2倍にしたときの電気量を求めよ。
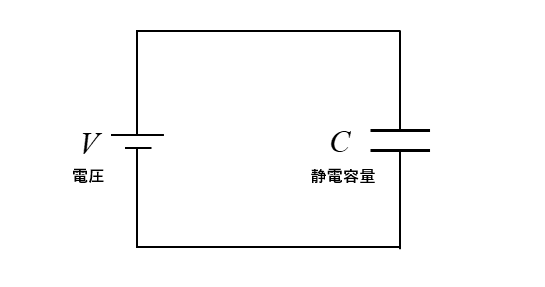
<解答例>
極板間隔を変更する前のコンデンサに貯まる電気量 \(Q\) は
\(Q=CV\) [C]
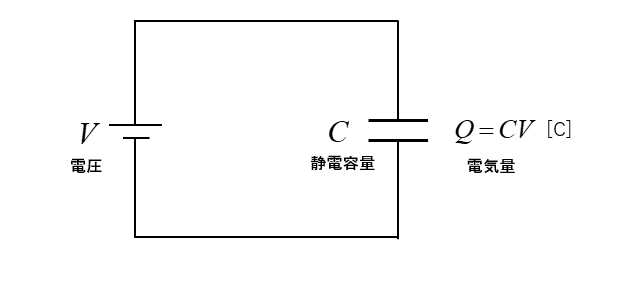
■ 極板間隔を2倍にした場合
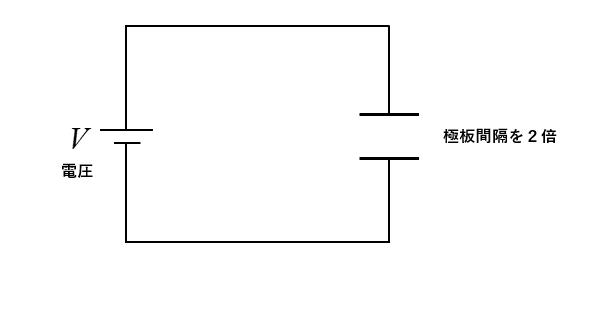
極板間隔を変えるとコンデンサの静電容量が変わります。
静電容量
\(C=ε\cfrac{S}{d}\) の式で極板間隔 \(d\) が2倍になるので
変化後の静電容量を \(C’\) とすると
\(C’=ε\cfrac{S}{2d}=\cfrac{1}{2}C\) [F]
静電容量は元の \(\cfrac{1}{2}\) になります。
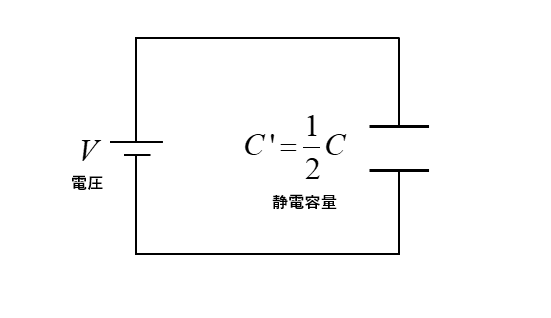
コンデンサに貯まる電気量 \(Q’\) は 電圧 \(V\) は変わらないので
\(Q’=C’V=\cfrac{1}{2}CV\) [C] になります。
コンデンサに貯まる電気量 \(Q’\) は
\(Q’=\cfrac{1}{2}CV\) [C] になります。
問題2
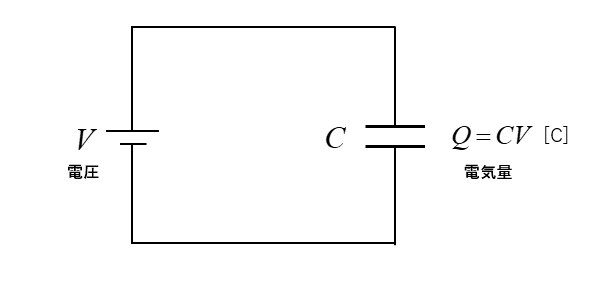
図のように静電容量 \(C\) のコンデンサに電圧 \(V\) を加えて、電気量 \(Q\) が蓄えられています。
次にコンデンサを電池から外して、極板間隔を2倍にしたときのコンデンサの電圧を求めよ。
<解答例>
★ 電池から外したコンデンサには
\(Q=CV\cdots(1)\) の電気量があります。
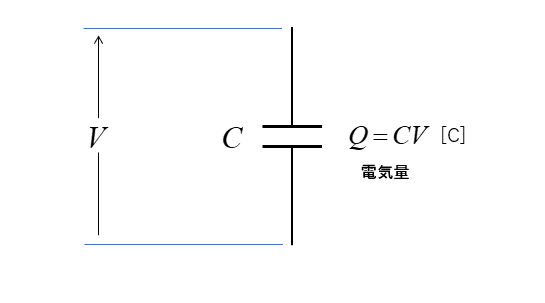
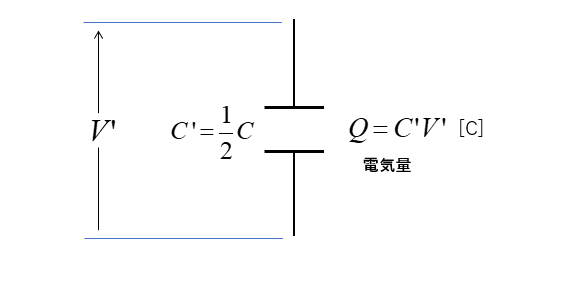
■ 極板間隔を2倍にした場合
電気量 \(Q\) は変わりませんが コンデンサの静電容量と電圧が変化します。
変化後の静電容量を \(C’\) 電圧を \(V’\) とすると 図のようになります。
\(Q=C’V’\cdots(2)\)
式(1)と式(2)は等しいので
\(CV=C’V’\)
\(CV=\cfrac{1}{2}CV’\)
\(V’=2V\) [V] になります。
以上で「コンデンサの基本式とコンデンサの特徴と役割」の説明を終わります。