- コンデンサの直列接続の、静電容量の求め方や直列接続の見分け方
- コンデンサの直列接続では、蓄えられる電荷が共通の値になる
- コンデンサの並列接続の、静電容量の求め方や並列接続の見分け方
- コンデンサの並列接続では、コンデンサに掛かる電圧が共通の値になる
について説明します。
コンデンサの直列接続の合成容量
コンデンサが2個の直列接続の合成容量
コンデンサの直列接続の合成容量は それぞれのコンデンサの 逆数の和 が 合成容量の逆数の和 になります。
\(\cfrac{1}{C}=\cfrac{1}{C_1}+\cfrac{1}{C_2}\) [F]
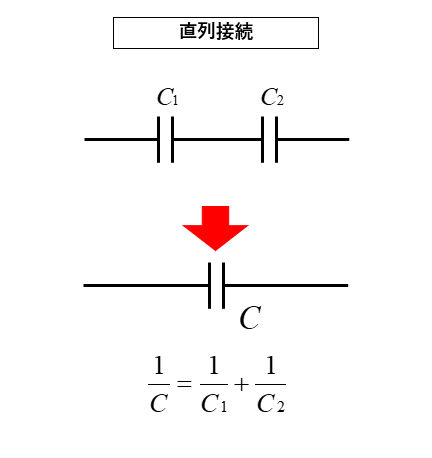
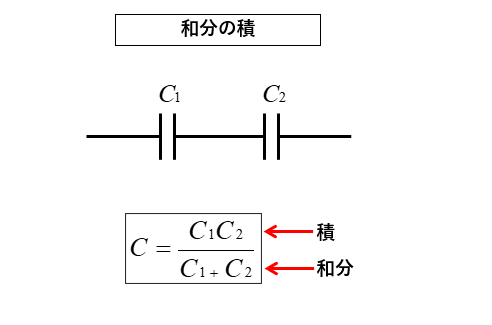
和分の積
コンデンサが2個直列接続のときは 和分の積 の公式が使えます。
\(C=\cfrac{C_1C_2}{C_1+C_2}\) [F]
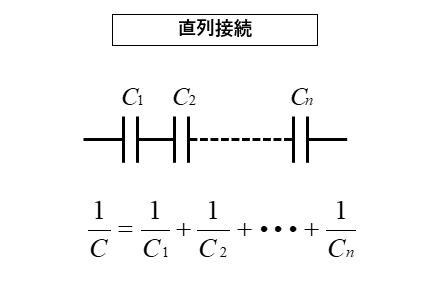
2個以上のコンデンサの直列接続の合成容量
コンデンサが2個以上、n個の場合の直列接続も基本的には2個の場合と同じようにできます。
\(\cfrac{1}{C}=\cfrac{1}{C_1}+\cfrac{1}{C_2}+\cdots+\cfrac{1}{C_n}\) [F]
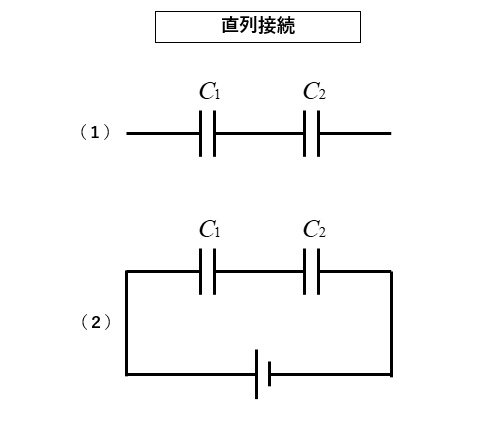
コンデンサの直列接続の見分け方
コンデンサの直列接続と並列接続を見分けるには 電位 を使うとわかり易いです。
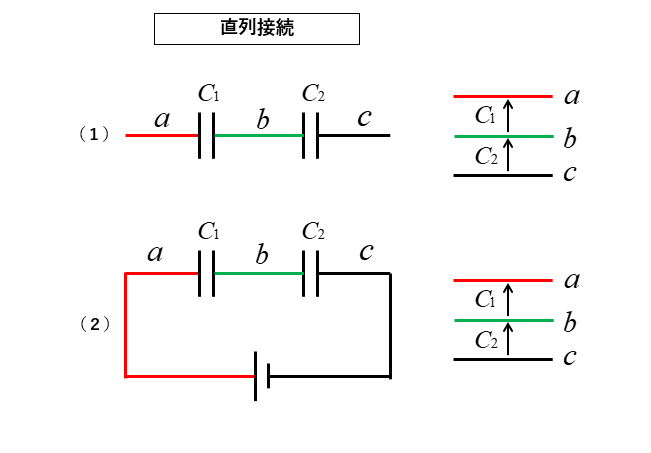
次の例は感覚的に直列接続と分かります。
■ 電位で考える
次の図のように 電位 を色分けして考えてみましょう。
abcのように色分けすることができますね。
\(C_1\) の電位 と \(C_2\) の電位が 直列になっているのがわかります。
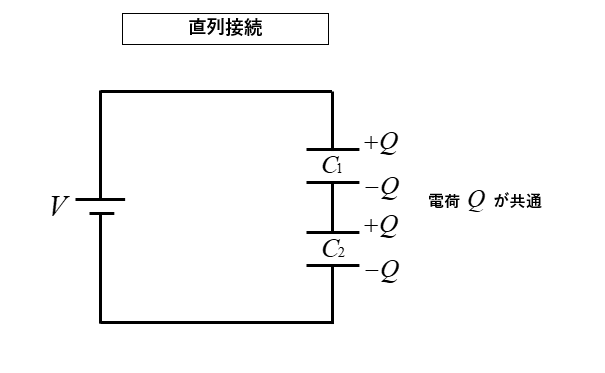
コンデンサの直列接続と電荷量
コンデンサの直列接続は 静電容量 \(C\) の大きさに関係なく 電荷量 \(Q\) が共通になります。
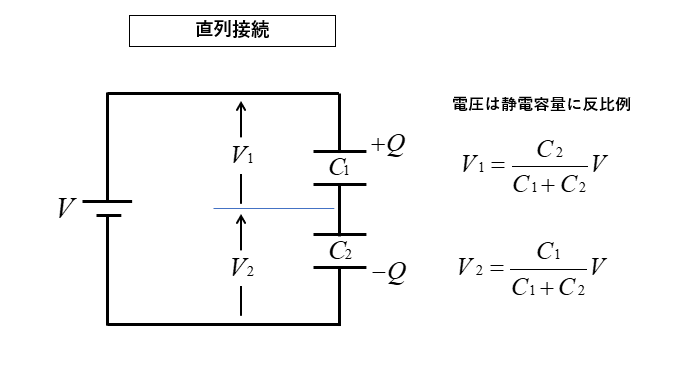
■ コンデンサの直列接続の 端子電圧 \(V_1、V_2\) は静電容量 \(C_1、C_2\) に反比例します。
\(V_1=\cfrac{C_2}{C_1+C_2}V\) [V]
\(V_2=\cfrac{C_1}{C_1+C_2}V\) [V]
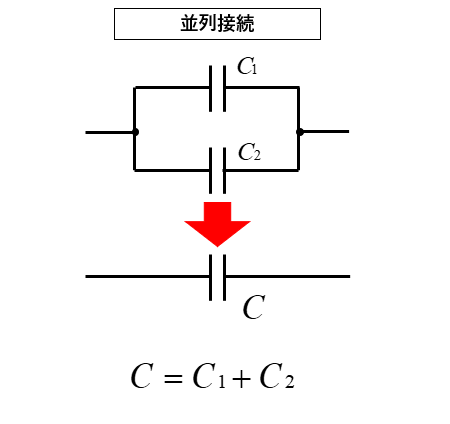
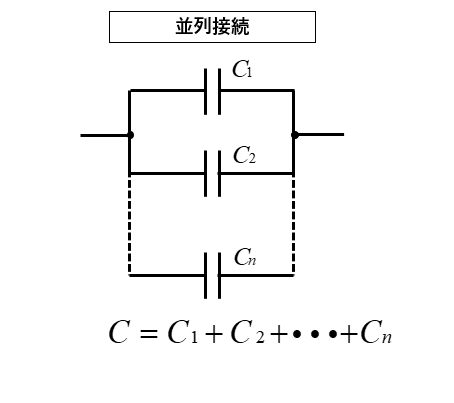
コンデンサの並列接続の合成容量
コンデンサが2個の場合の並列接続の合成容量
■ コンデンサの並列接続の合成容量は それぞれのコンデンサの足し算が 合成容量 になります。
\(C=C_1+C_2\) [F]
2個以上のコンデンサの並列接続の合成容量
コンデンサが2個以上、n個の場合の並列接続も基本的には2個の場合と同じようにできます。
\(C=C_1+C_2+\cdots+C_n\) [F]
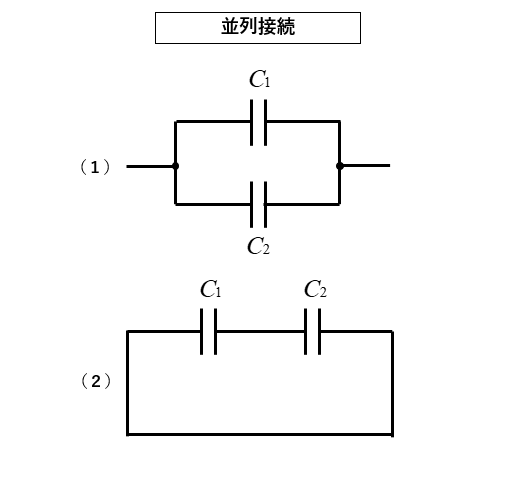
コンデンサの並列接続の見分け方
次は並列接続の例です。
(1)は並列だということが感覚的にわかります。
しかし、(2)は直列にも見えますね。
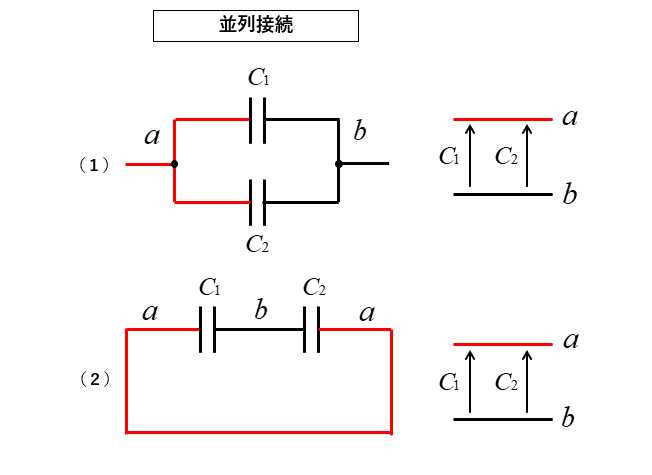
■ 電位で考えると分かりやすい
次の図のように 電位 を色分けして考えてみましょう。
abのように色分けすることができますね。
abの電位の通り道が \(C_1\) の ルートと \(C_2\) の ルートがあります。
つまり 並列 ということになります。
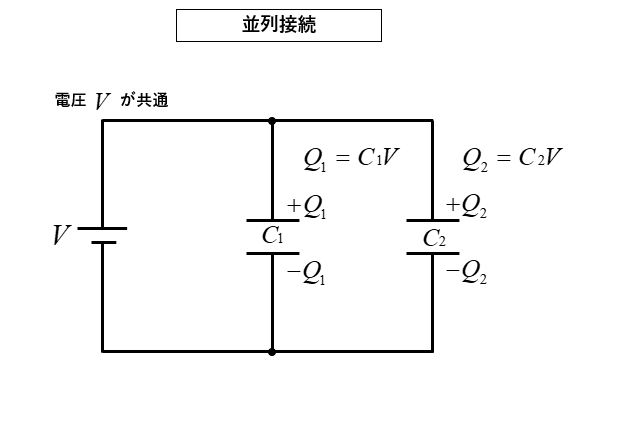
コンデンサの並列接続と電荷量
コンデンサの並列接続はコンデンサに掛かる 電圧 が共通になります。
\(Q_1=C_1V\) [C]
\(Q_1=C_1V\) [C]
■ 例題1
静電容量 \(C_1\) と \(C_2\) をそれぞれ電圧 \(V_1\) と \(V_2\) で充電しました。
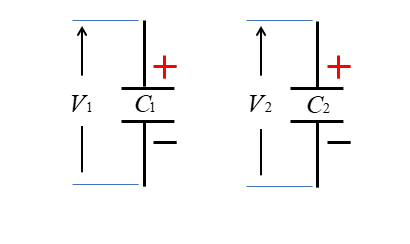
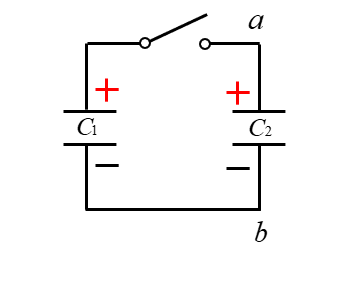
■ 図のように \(C_1\) と \(C_2\) を接続し、スイッチを入れて十分に時間が経過したときの、bに対する aの電位を求めよ。
<解答例>
スイッチを閉じると、図のようになります。
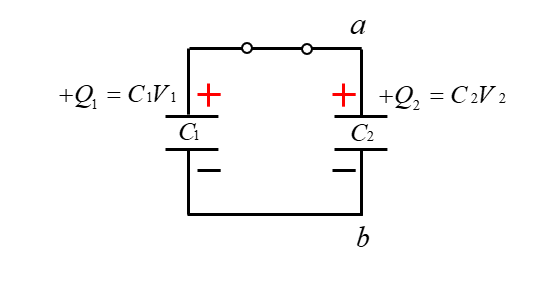
コンデンサは並列接続なので合成容量 \(C\) は
\(C=C_1+C_2\)
電荷量 \(Q\) は
\(Q=Q_1+Q_2\)
等価回路は次のようになります。
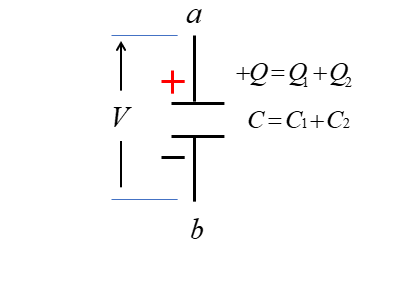
aの電位 \(V\) は \(Q=CV\) の コンデンサ式から
\(V=\cfrac{Q}{C}\)
\(V=\cfrac{Q_1+Q_2}{C_1+C_2}\)
\(V=\cfrac{C_1V_1+C_2V_2}{C_1+C_2}\) [V] になります。
■ 例題2
静電容量 \(C_1\) と \(C_2\) をそれぞれ電圧 \(V_1\) と \(V_2\) で充電しました。
ただし \(C_1V_1>C_2V_2\) とします。
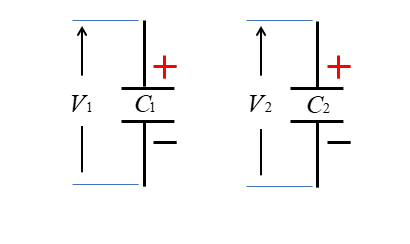
■ 図のように \(C_1\) と \(C_2\) を接続し、スイッチを入れて十分に時間が経過したときの、bに対する aの電位を求めよ。 (\(C_2\) の極性に注意!)
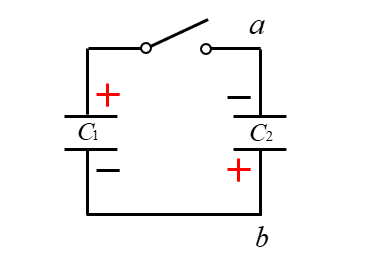
<解答例>
スイッチを閉じると、図のようになります。
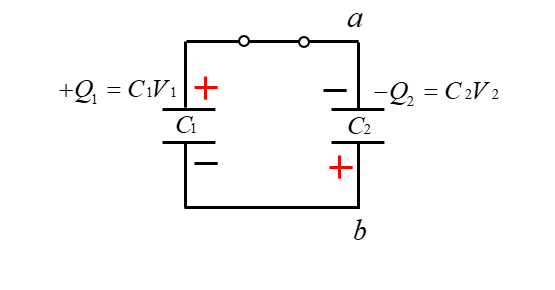
コンデンサは並列接続なので合成容量 \(C\) は
\(C=C_1+C_2\)
電荷量 \(Q\) は
\(Q=+Q_1-Q_2\)
等価回路は次のようになります。
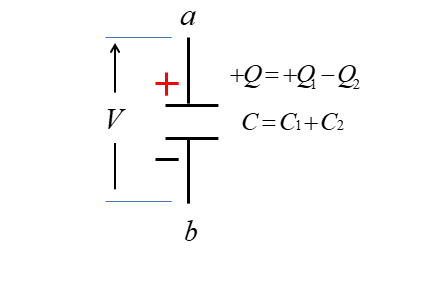
aの電位 \(V\) は \(Q=CV\) の コンデンサ式から
\(V=\cfrac{Q}{C}\)
\(V=\cfrac{Q_1-Q_2}{C_1+C_2}\)
\(V=\cfrac{C_1V_1-C_2V_2}{C_1+C_2}\) [V] になります。
コンデンサの静電容量については コンデンサの基本式 を参照してください。
練習問題1
問題を理解するために数値を入れて計算してみます。
実際の静電容量は [F] でなく [μF] のように非常に小さい数値になります。計算上のものとして考えてください。
問題1
それぞれのコンデンサを図のように、充電しました。
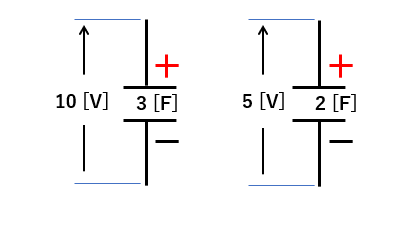
図のようにコンデンサを接続して十分な時間が経過したときの bに対する aの電位を求めよ。
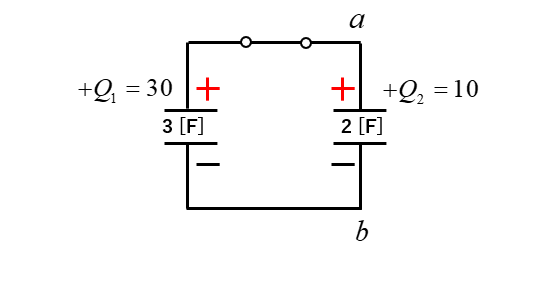
\(V=\cfrac{Q}{C}\) の公式から
\(V=\cfrac{30+10}{3+2}\) [V]
aの電位は次のようになります。
\(V=8\) [V]
問題2
それぞれのコンデンサを図のように、充電しました。

図のような極性でコンデンサを接続しました。
十分な時間が経過したときの bに対する aの電位を求めよ。
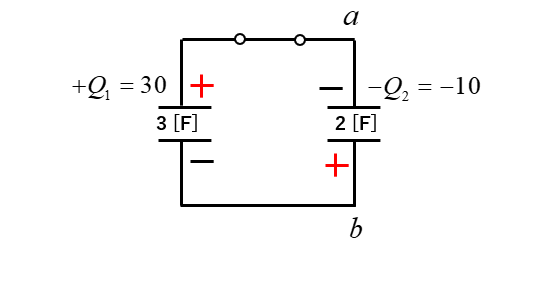
\(V=\cfrac{Q}{C}\) の公式から
\(V=\cfrac{30-10}{3+2}\) [V]
aの電位は次のようになります。
\(V=4\) [V]
問題3
図の回路において、各コンデンサに蓄えられている電気量を求めよ。
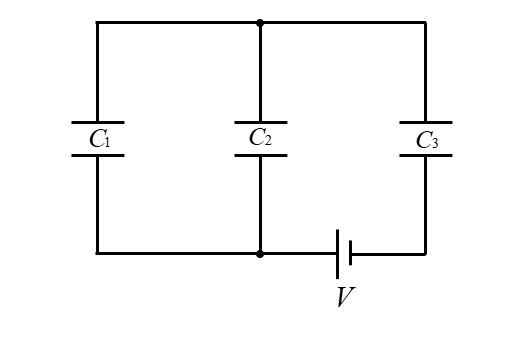
<解答例>
問題を見やすいように変形します。
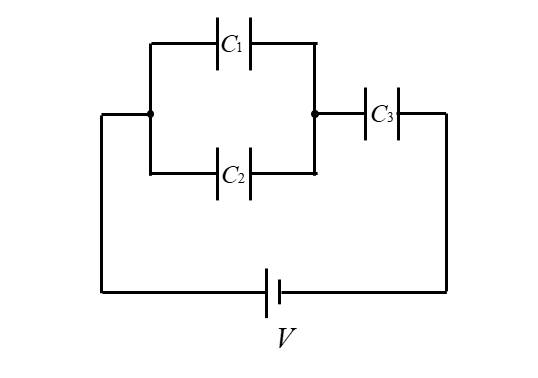
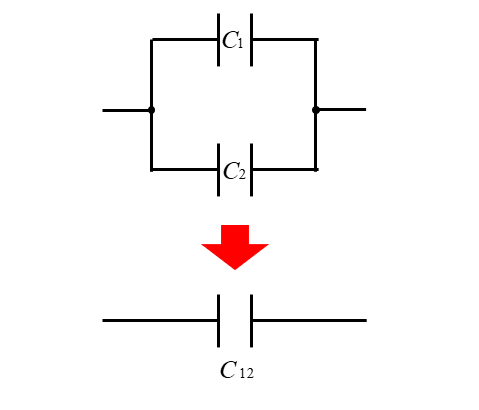
■ \(C_1\) と \(C_2\) の合成容量を \(C_{12}\) とすると
\(C_{12}=C_1+C_2\)
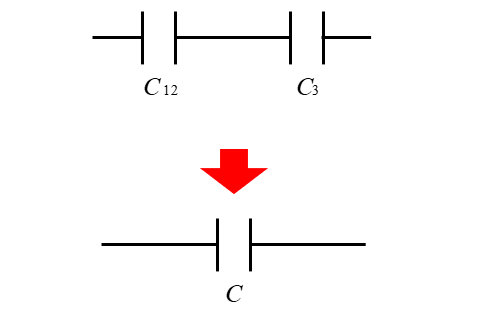
■ 回路全体の合成容量を \(C\) とすると
\(C=\cfrac{(C_1+C_2)C_3}{C_1+C_2+C_3}\)
■ 全体の電荷量
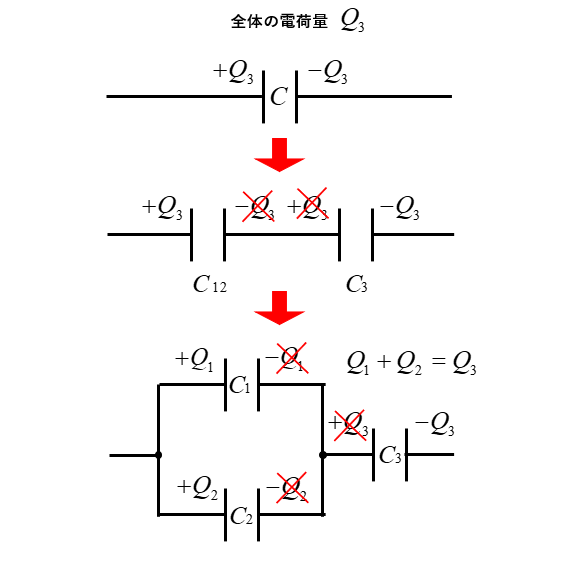
図のように、電荷と電圧を設定します。
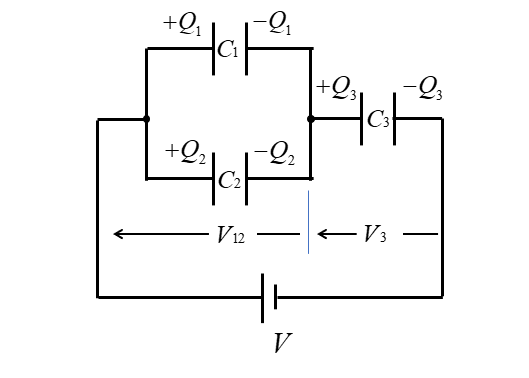
電荷 \(Q_1、Q_2、Q_3\) には
\(Q_1+Q_2=Q_3\) の関係があります。
\(Q=CV\) の公式から
\(Q_3=\cfrac{(C_1+C_2)C_3}{C_1+C_2+C_3}V\)
\(C_1\) と \(C_2\) に掛かる電圧 \(V_{12}\) は
\(V_{12}=\cfrac{C_3}{C_1+C_2+C_3}V\) になります。
\(C_1\) に蓄えられる電気量は
\(Q_1=C_1V_{12}=\cfrac{C_1C_3}{C_1+C_2+C_3}V\)
\(C_2\) に蓄えられる電気量は
\(Q_2=C_2V_{12}=\cfrac{C_2C_3}{C_1+C_2+C_3}V\)
\(C_1\) に蓄えられる電気量は
\(Q_1=\cfrac{C_1C_3}{C_1+C_2+C_3}V\) [C]
\(C_2\) に蓄えられる電気量は
\(Q_2=\cfrac{C_2C_3}{C_1+C_2+C_3}V\) [C]
\(C_3\) に蓄えられる電気量は
\(Q_3=\cfrac{(C_1+C_2)C_3}{C_1+C_2+C_3}V\) [C]
問題4
\(S_1\) のスイッチを閉じたときの cに対する bの電位を求めよ。
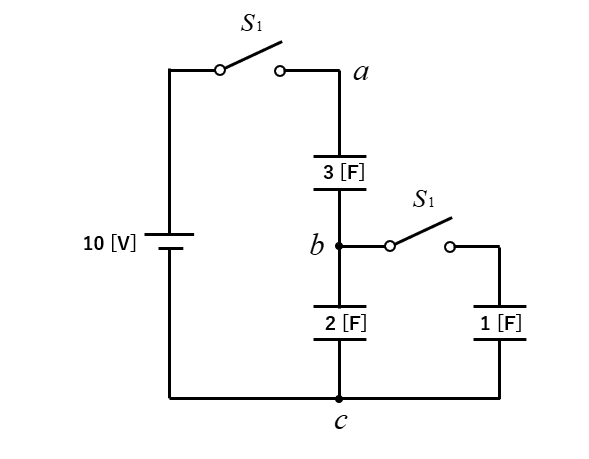
<解答例>
\(S_1\) のスイッチを閉じたときの回路図は、次のようになります。
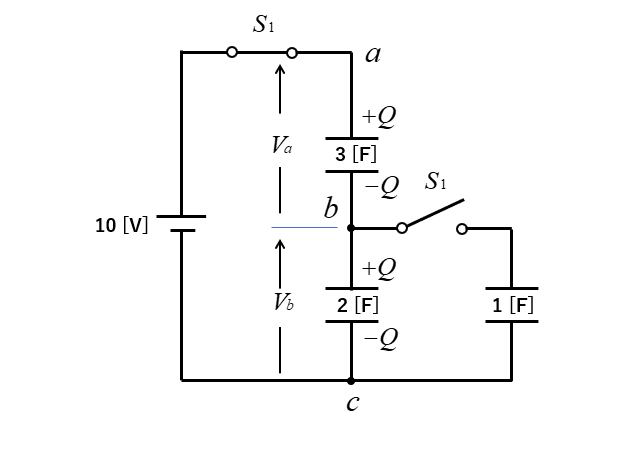
直列接続なのでコンデンサに貯まる電荷 \(Q\) は
\(Q=CV\) から
\(Q=\cfrac{3×2}{3+2}×10=12\) [C]
bの電位 \(V_2\) は
\(V_b=\cfrac{Q}{2}=\cfrac{12}{2}=6\) [V]
\(V_b=6\) [V] になります。
問題5
次に、問題1の回路で \(S_1\) のスイッチを開いて \(S_2\) のスイッチを閉じたときの aの電位を求めよ。
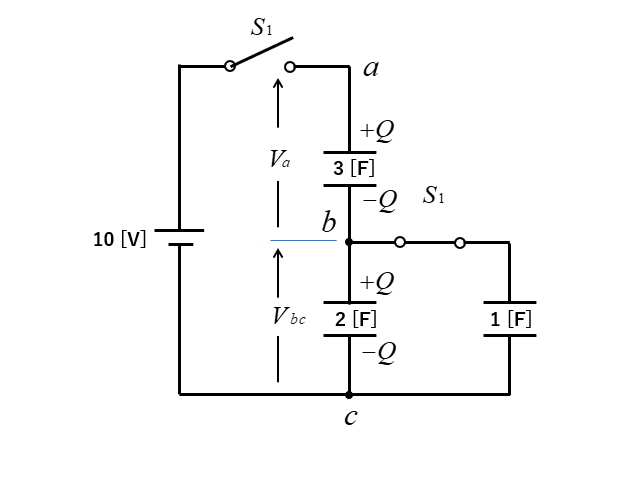
<解答例>
bc間の電位を \(V_{bc}\) とする \(Q\) は変わらないので
\(V_{bc}=\cfrac{Q}{2+1}=\cfrac{12}{3}=4\) [V]
\(V_a=\cfrac{Q}{3}=\cfrac{12}{3}=4\) [V]
aの電位はac感の電位差になりますので
\(V_a+V_{bc}=8\) [V] になります。
以上で「コンデンサの直列接続とコンデンサの並列接続」の説明を終わります。