コンデンサの容量計算方法は
コンデンサが直列接続の場合、並列接続の場合によって計算方法が違います。
コンデンサの合成静電容量の計算方法について説明します。
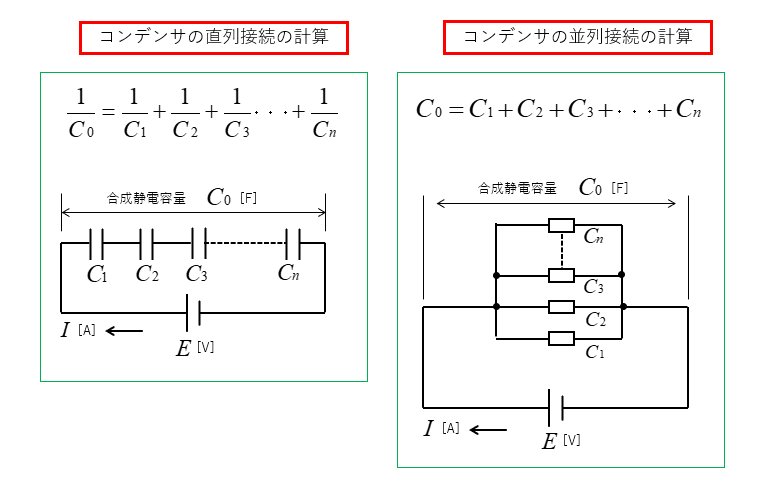
コンデンサの合成静電容量
コンデンサの合成容量計算の方法は、次のようになります。
合成静電容量の計算式

合成抵抗の計算方法と比べてみます。
■ 合成抵抗の計算式
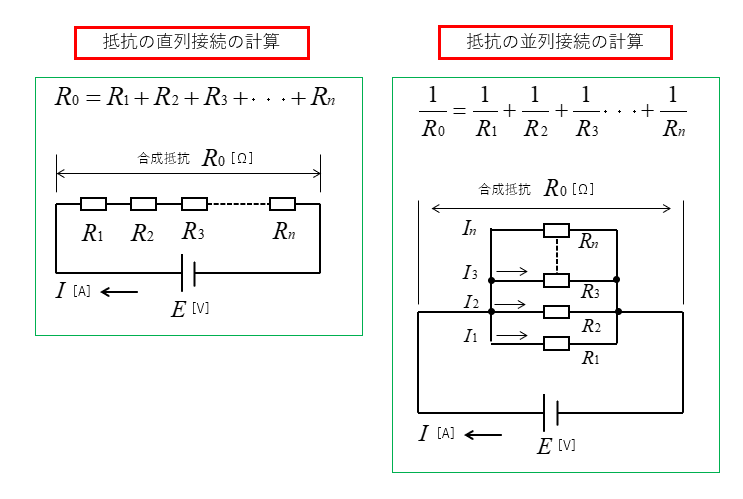
コンデンサの直列接続と並列接続の計算式は、抵抗の直列接続と並列接続の計算式の逆になります。
| コンデンサ(F) | 抵抗(Ω) | |
|---|---|---|
| 直列接続 | \(\cfrac{1}{C}=\cfrac{1}{C_1}+\cfrac{1}{C_2}+\cfrac{1}{C_3}+\cdots+\cfrac{1}{C_n}\) | \(R=R_1+R_2+R_3+・・・+R_n\) |
| 並列接続 | \(C=C_1+C_2+C_3+・・・+C_n\) | \(\cfrac{1}{R}=\cfrac{1}{R_1}+\cfrac{1}{R_2}+\cfrac{1}{R_3}+\cdots+\cfrac{1}{R_n}\) |
コンデンサの直列接続で合成静電容量が減少する理由
静電容量が等しいコンデンサ \(C_1\) [F] を
2個直列に接続した時の合成静電容量は
\(C=\cfrac{1}{2}C_1\) [F] になります。
これは。平行板コンデンサの静電容量 \(C\) は
\(C=ε\cfrac{S}{d}\) で
直列にすることにより電極の間隔 \(d\) が 2倍になるためです。
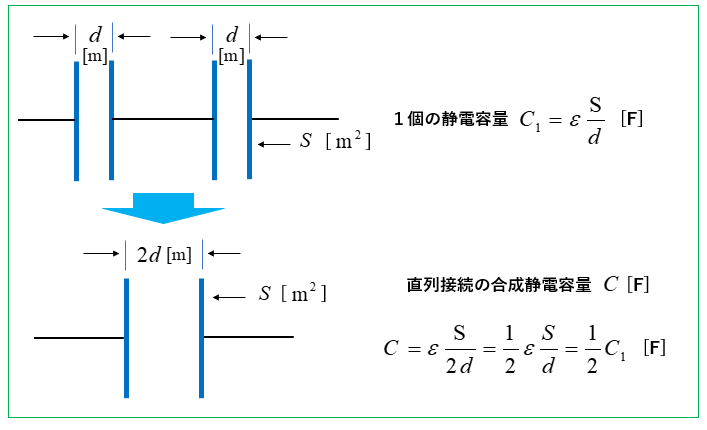
コンデンサを2個の直列接続
コンデンサを2個の直列接続したときの合成静電容量は 和分の積の公式 が使えます。
和分の積の公式
\(C=\cfrac{C_1C_2}{C_1+C_2}\) [F]
コンデンサの2個以上の直列接続の合成静電容量
コンデンサの直列接続の合成容量は、それぞれの静電容量の逆数の和になります。
\(\cfrac{1}{C}\)\(=\cfrac{1}{C_1}+\cfrac{1}{C_2}+\cfrac{1}{C_3}+\cdots+\cfrac{1}{C_n}\) [F]
直列につながれたそれぞれのコンデンサに貯まる電荷 \(Q\) はすべて等しい。
電圧 \(V\) は各コンデンサにかかる電圧の合計になります。
コンデンサの直列接続では
各コンデンサに貯まる電荷は同じになります。
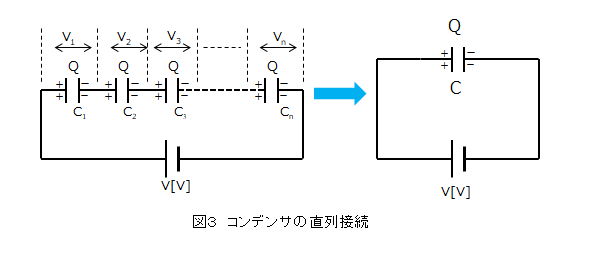
\(Q=CV\) から \(V=\cfrac{Q}{C}\)
\(V=V_1+V_2+V_3+\cdots+V_n\)
\(V=\cfrac{Q}{C_1}+\cfrac{Q}{C_2}+\cfrac{Q}{C_3}+\cdots+\cfrac{Q}{C_n}=\cfrac{Q}{C}\)
両辺を \(Q\) で割ると
\(\cfrac{1}{C}=\cfrac{1}{C_1}+\cfrac{1}{C_2}+\cfrac{1}{C_3}+\cdots+\cfrac{1}{C_n}\)
コンデンサの分圧式
コンデンサの直列接続の分圧式の求め方は、抵抗の並列接続の分流式と似ています。
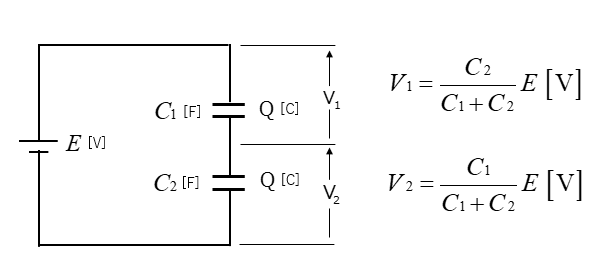
コンデンサの直列接続では、蓄えられる電荷の値が同じということを、利用して分圧式を求めます。
コンデンサの分圧式
\(V_1=\cfrac{C_2}{C_1+C_2}E\) [V]
\(V_2=\cfrac{C_1}{C_1+C_2}E\) [V]
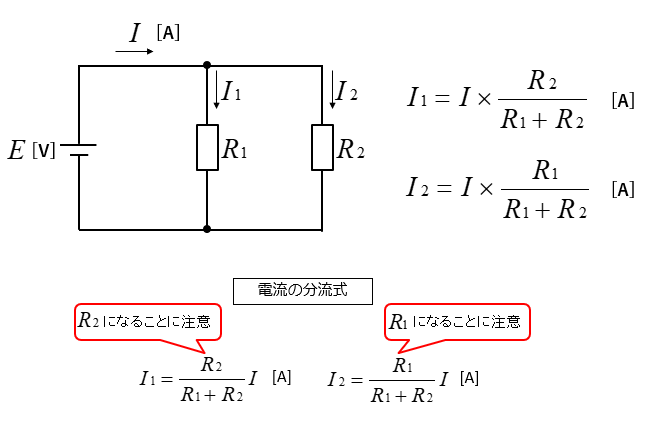
抵抗の分流式
\(I_1=\cfrac{R_2}{R_1+R_2}I\) [V]
\(I_2=\cfrac{R_1}{R_1+R_2}I\) [V]
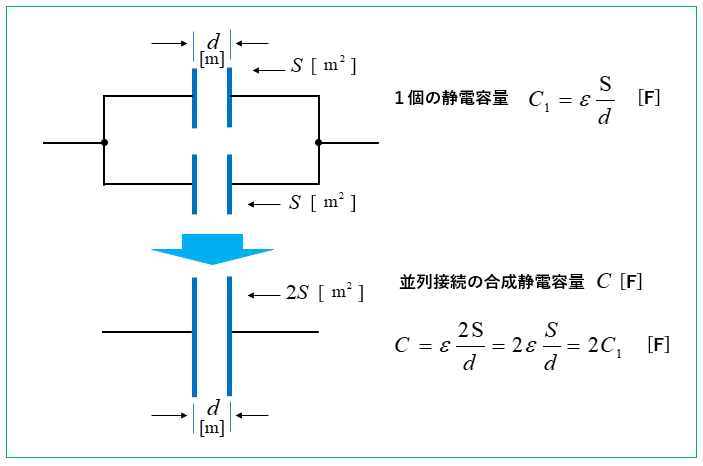
コンデンサの並列接続で合成静電容量が増加する理由
静電容量が等しいコンデンサ \(C_1\) [F] を2個並列に接続した時の、合成静電容量は
\(C=2C_1\) [F] になります。
これは。平行板コンデンサの静電容量 \(C\) は
\(C=ε\cfrac{S}{d}\) で、並列にすることにより電極の面積 \(S\) が 2倍になるためです。
コンデンサの並列接続の合成容量
コンデンサの並列接続の合成容量は、それぞれの静電容量の和になります。
\(C=C_1+C_2+C_3+・・・\)\(+C_n\) [F]
全体にたくわえられる電荷 Q はそれぞれのコンデンサに貯められる電荷の合計になります。
コンデンサの並列接続では
各コンデンサにかかる電圧は同じになります。
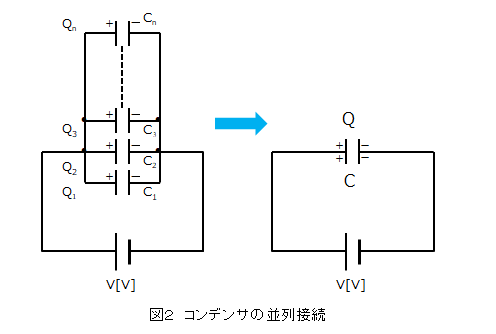
各コンデンサにかかる電圧は同じです。
\(Q=CV\) から
\(Q=Q_1+Q_2+Q_3+\cdots+Q_n\)
\(Q=C_1V+C_2V+C_3V+\cdots\)\(+C_nV\)
\(Q=(C_1+C_2+C_3+\cdots\)\(+C_n)V=CV\) とすると
\(C=C_1+C_2+C_3+\cdots\)\(+C_n\) となります。
コンデンサの公式
静電容量 \(C\) は、コンデンサが電荷 \(Q\) を 蓄える能力 を表しています。
図のようなコンデンサに \(V\) の電圧を加えると、コンデンサには電荷 \(Q\) が貯まります。
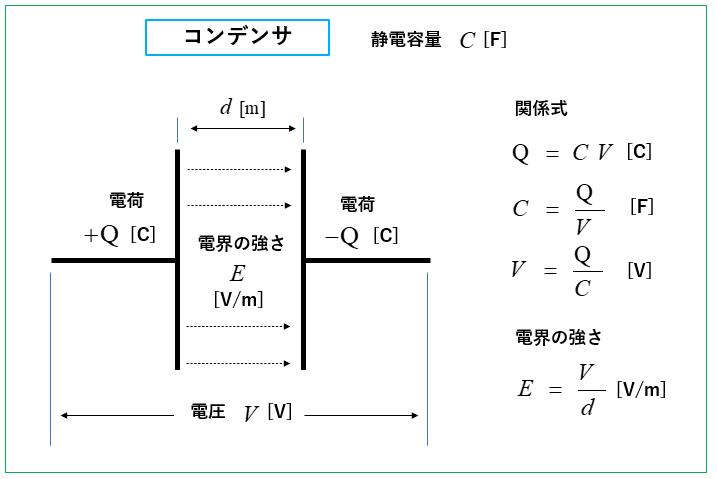
コンデンサの関係式
■ 電荷
\(Q=CV\) [F]
■ 静電容量
\(C=\cfrac{Q}{V}\) [F]
静電容量 \(C\) は定数で電圧が \(1V\) のときに、蓄えられる電荷量を表します。
\(C=\cfrac{Q}{V}=\cfrac{Q}{1}=Q\) [C]
■ 電圧
\(V=\cfrac{Q}{C}\) [V]
■ 電界の強さ
\(E=\cfrac{V}{d}\) [V/m]
■ コンデンサの分圧式
\(V_1=\cfrac{C_2}{C_1+C_2}E\) [V]
\(V_2=\cfrac{C_1}{C_1+C_2}E\) [V]
練習問題
問題1
コンデンサが図のように接続された回路の合成静電容量 \(C\) を求めよ。
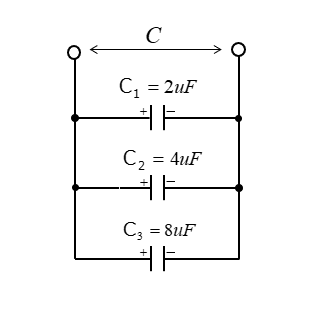
<解答例>
コンデンサの並列接続の合成静電容量 \(C\) は加算すれば良いので、次のようになります。
\(C=C_1+C_2+C_3=2+4+8=14\) [uF]
問題2
コンデンサが図のように直列に接続された回路の合成静電容量 \(C\) を求めよ
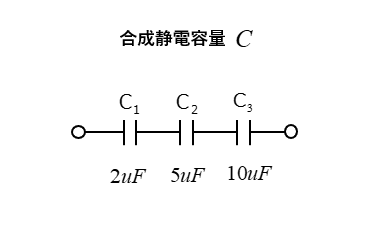
<解答例>
コンデンサの直列接続の合成静電容量 \(C\) は
それぞれの静電容量の逆数の和になるので、次のようになります。
\(\cfrac{1}{C}=\cfrac{1}{C_1}+\cfrac{1}{C_2}+\cfrac{1}{C_3}\)
\(\cfrac{1}{C}=\cfrac{1}{2}+\cfrac{1}{5}+\cfrac{1}{10}\)
\(\cfrac{1}{C}\)\(=\cfrac{5}{10}+\cfrac{2}{10}+\cfrac{1}{10}\)\(=\cfrac{8}{10}=\cfrac{4}{5}\)
\(\therefore C=\cfrac{5}{4}=1.25\) [uF]
以上で「コンデンサの容量計算」の説明を終わります。