平行板コンデンサの中に導体や誘電体を挿入すると、電界や電位がどのように変化するのかを説明します。
コンデンサの関係式
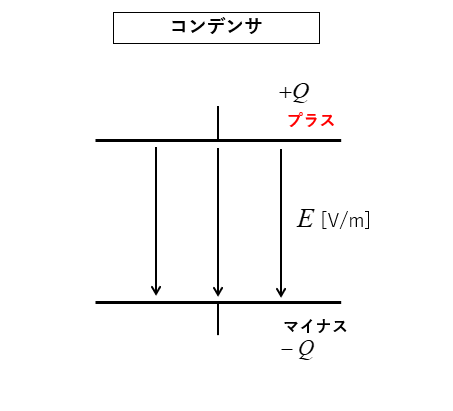
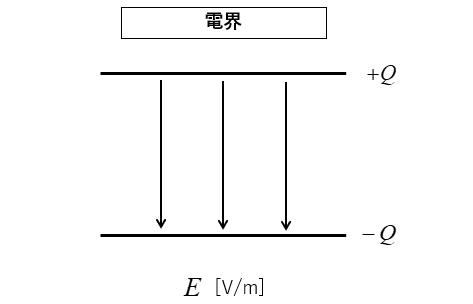
■ 図のようなコンデンサが \(Q\) [C] の電荷に帯電しています。
極板間には一様な電界 \(E\) [V/m] が発生しています。
コンデンサには次のような関係式があります。
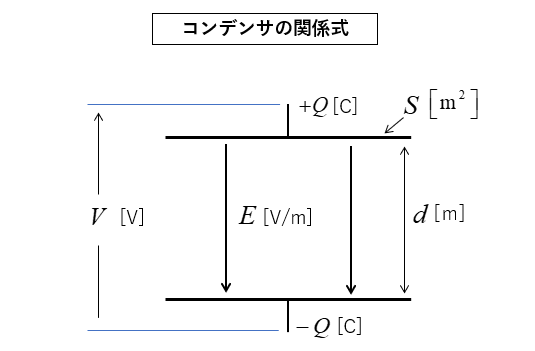
コンデンサの関係式
- \(C= ε\cfrac{S}{d}\) [F]
- \(Q=CV\) [C]
- \(V=Ed\) [V]
- \(C\cdots\)静電容量 [F]
- \(S\cdots\)極板の面積 [m2]
- \(d\cdots\)極板間の距離 [m]
- \(V\cdots\)極板間の電圧 [V]
コンデンサに導体を挿入した場合
コンデンサに導体を挿入すると、導体の自由電子が移動します。
自由電子の移動により導体には、コンデンサの電界を打ち消すような電界が発生します。
導体の内部の電界がゼロになるような電界が発生します。
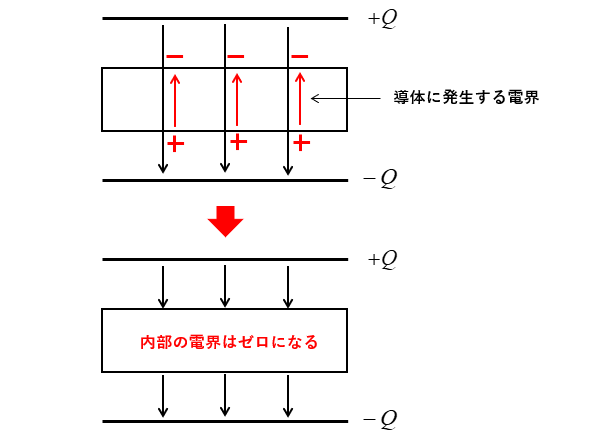
電界に沿って電荷が移動する現象を 静電誘導 といいます。
極板間が真空の静電容量
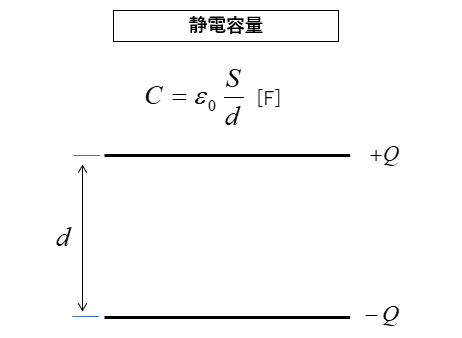
コンデンサ内部が真空の静電容量は、次の式になります。
\(C=ε_0\cfrac{S}{d}\) [F]
導体を挿入した静電容量
厚さが \(d_1\) の導体を挿入したコンデンサの静電容量は、次の式になります。
\(C=ε_0\cfrac{S}{d-d_1}\) [F]
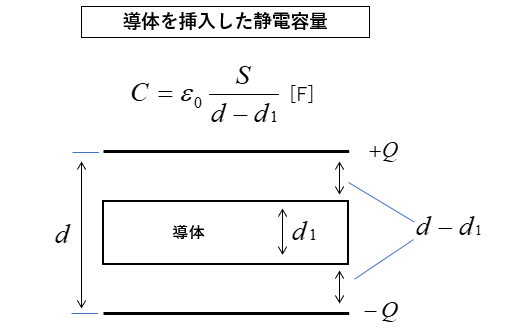
図のように導体を移動しても静電容量は変わらない。
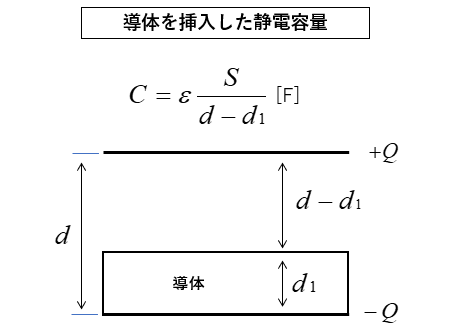
コンデンサに誘電体を挿入した場合
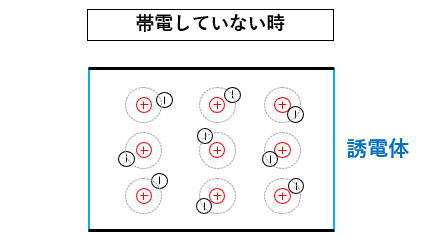
コンデンサが帯電していないときに、誘電体を挿入します。
誘電体(絶縁体) の電子はバラバラになっています。
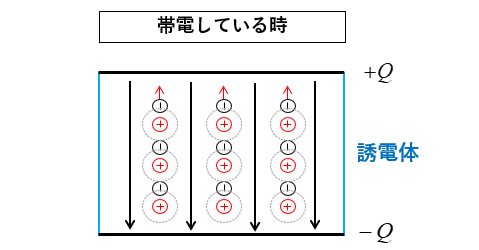
コンデンサに誘電体を挿入して、電荷に帯電していると誘電体の中で電極がそろいます。
このように、プラスとマイナスが分かれることを 誘電分極 といいます。
ただし、自由電子のように原子の外に飛び出すことはできません。
電極間が真空のときの電界の強さ
真空のときの電界の強さは、次の式になります。
\(E=k\cfrac{Q}{r^2}\) [V/m]
\(E=\cfrac{1}{4πε_0}×\cfrac{Q}{r^2}\) [V/m]
誘電体を挿入したときの電界の強さ
誘電率 \(ε\) の誘電体が挿入されたときの電界の強さは、次の式になります。
\(E’=\cfrac{1}{4πε_0ε_r}×\cfrac{Q}{r^2}\) [V/m]
\(E’=\cfrac{1}{ε_r}×E\) [V/m]
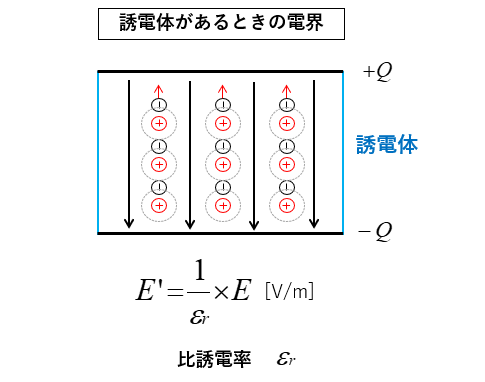
誘電体を挿入したときの電界の強さは
真空のときの電界の強さの \(\cfrac{1}{ε_r}\) 倍になります。
定数 \(k\) と 誘電率
誘電率は電荷の貯めやすさの比率を表します。
\(k=\cfrac{1}{4\piε_0}=9×10^9\) [N・m2/C2]\(\cdots\)定数
\(ε_0=8.854×10^{-12}\) [F/m]\(\cdots\)真空の誘電率
\(ε=ε_0ε_r\) [F/m]\(\cdots\)誘電率で「イプシロン」と読みます。
\(ε_r=\cfrac{ε}{ε_0}\)\(\cdots\)比誘電率 空気中では \(ε_r=1\) です。
誘電体を挿入したときのコンデンサ内部の電界と電位
誘電体を挿入する前のコンデンサは図のようになります。

誘電体を挿入した場合は次のようになります。
誘電体の大きさは極板間隔の \(\cfrac{1}{2}\) 倍 、比誘電率 \(ε_r=3\) とします。
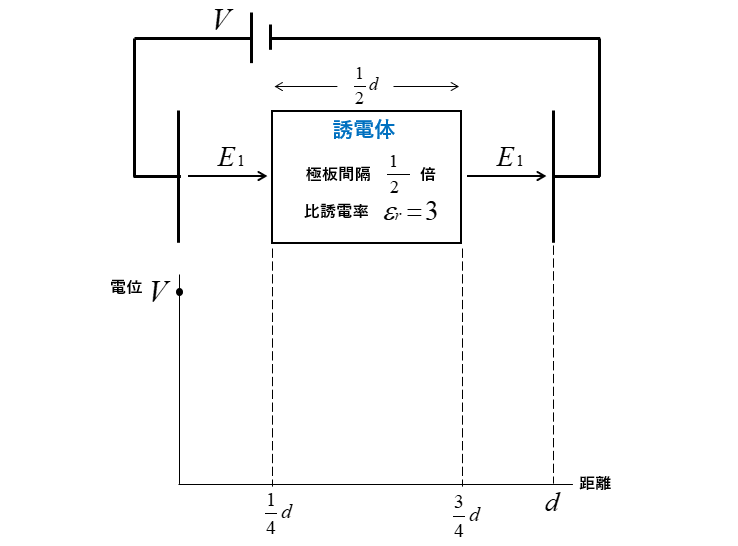
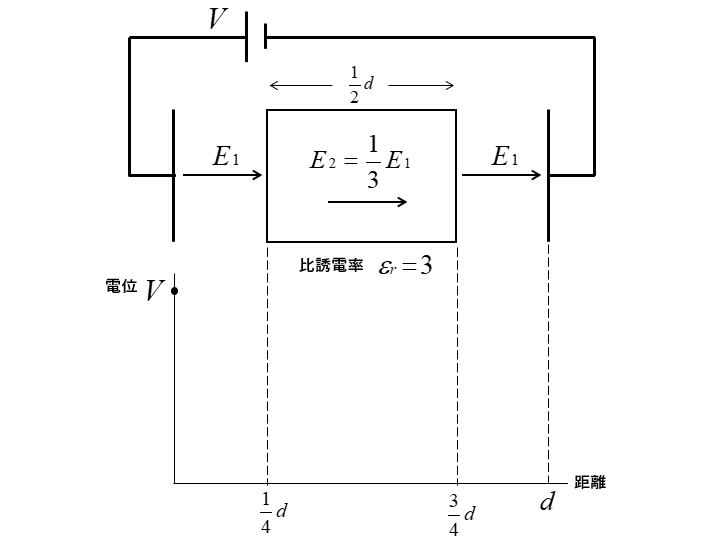
誘電体の外部の電界の強さを \(E_1\) とすると
誘電体の内部の電界の強さ \(E_2\) は 次のようになります。
\(E_2=\cfrac{1}{ε_r}E_1\) [V/m]
\(E_2=\cfrac{1}{3}E_1\cdots(1)\) [V/m]
電位の関係式
\(E_2=\cfrac{1}{3}E_1\cdots(1)\) [V/m]
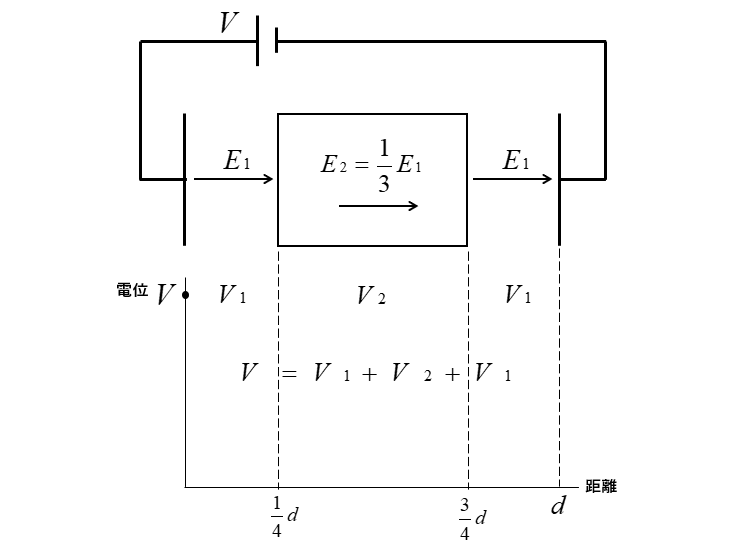
■ 電位と電界の関係式から
\(V=Ed\)
\(V=E_1\cfrac{1}{4}d+E_2\cfrac{1}{2}d+E_1\cfrac{1}{4}d\cdots(2)\)
式(2)に式(1)を代入して計算します。
\(V=E_1\cfrac{1}{4}d+\cfrac{1}{3}E_1×\cfrac{1}{2}d+E_1\cfrac{1}{4}d\cdots(2)\)
\(E_1=\cfrac{3V}{2d}\)
\(E_2=\cfrac{V}{2d}\)
電界 \(E_1\) の電位 \(V_1\) は
\(V_1=E_1×\cfrac{d}{4}=\cfrac{3V}{2d}×\cfrac{d}{4}=\cfrac{3}{8}V\)
\(V_1=\cfrac{3}{8}V\)
電界 \(E_2\) の電位 \(V_2\) は
\(V_2=E_2×\cfrac{d}{2}=\cfrac{V}{2d}×\cfrac{d}{2}=\cfrac{1}{4}V\)
\(V_2=\cfrac{1}{4}V\)
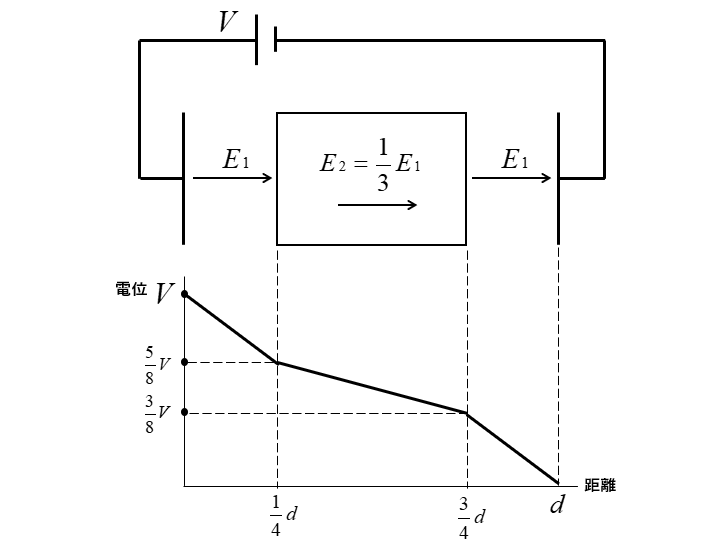
距離 \(\cfrac{1}{4}d\) の電位は
\(V-V_1=\cfrac{8}{8}V-\cfrac{3}{8}V=\cfrac{5}{8}V\) になります。
距離 \(\cfrac{3}{4}d\) の電位は
\(V-V_1-V_2=\cfrac{8}{8}V-\cfrac{3}{8}V-\cfrac{1}{4}V=\cfrac{3}{8}V\) になります。
以上で「コンデンサに導体・誘電体を挿入する」の説明を終わります。