この記事では
- コンデンサの静電容量と平行板コンデンサの公式
- 帯電体が他の物体を帯電させる静電誘導作用
- 帯電の仕組み
- 保存力とは何か
について説明します。
静電容量とはコンデンサ等においてどの位の電気量を蓄えられるかを示す量のことです。
記号に C を用い単位に [F] ファラドを使います。
平行板コンデンサの静電容量
図のような、電極の面積を \(S\) [m2]
電極間の距離を \(d\) [m]
誘電体を \(ε\) [F/m] とする平行板コンデンサがあります。

平行板コンデンサの静電容量は、次のようになります。
\(C=ε\cfrac{S}{d}\) [F]
■ 定数 \(k\) と 誘電率
誘電率は電荷の貯めやすさの比率を表します。
\(k=\cfrac{1}{4\piε_0}=9×10^9\) [N・m2/C2]\(\cdots\)定数
\(ε_0=8.854×10^{-12}\) [F/m]\(\cdots\)真空の誘電率
\(ε=ε_0ε_r\) [F/m]\(\cdots\)誘電率で「イプシロン」と読みます。
\(ε_r=\cfrac{ε}{ε_0}\)\(\cdots\)比誘電率 空気中では \(ε_r=1\) です。
\(k=\cfrac{1}{4\piε}\cdots\)誘電率εの媒質中の定数
■ 静電容量の公式は駐車場と磁石に例えると分かりやすい
\(C=ε\cfrac{S}{d}\) [F]
静電容量の大きさは
面積 \(S\) に比例し
電極の距離 \(d\) に反比例します。
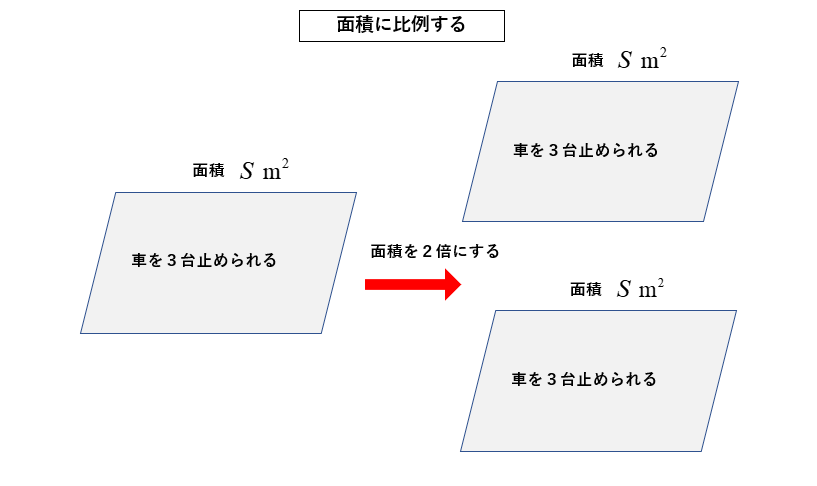
■ 面積に比例
面積 \(S\) の駐車場に車が3台止められるとすれば、面積を2倍にしたら車が6台止められることになります。
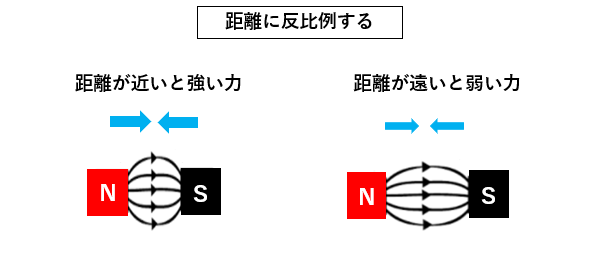
■ 電極間の距離に反比例
これは、磁石の吸引力に結びつけると覚えやすいです。磁石の吸引力は、距離が近くなりほど強くなります。
コンデンサに蓄えられる電気量をQとすると コンデンサの基本式 から
\(Q=CV\) [C] になります
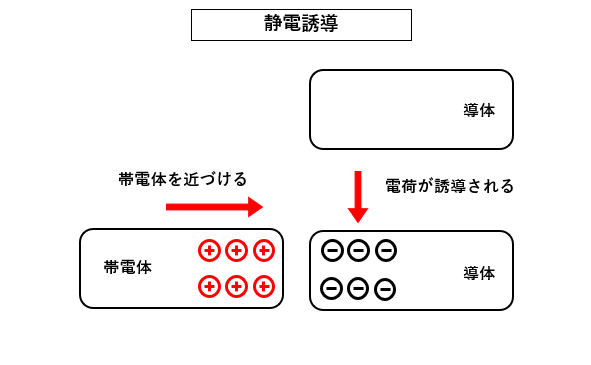
静電誘導作用とは
導体が電気を帯びることを 帯電 するといいます。
プラスの帯電体を近づける
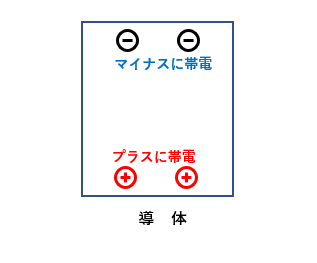
図のように 帯電していない導体があります。
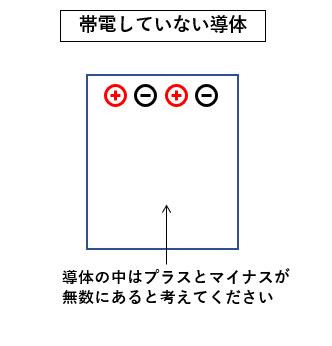
プラスの帯電体を、帯電していない導体に近づけます。
帯電体のプラスと導体のマイナスが吸引力で、電子が上にへ移動します。
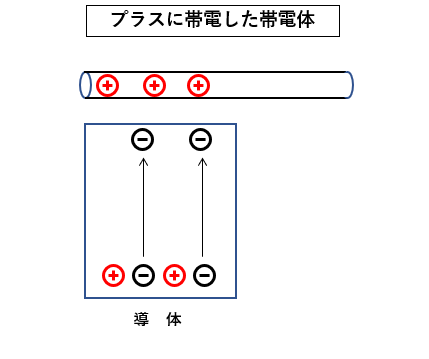
導体の上側がマイナスに、下側がプラスに帯電します。
マイナスの電荷を近づける
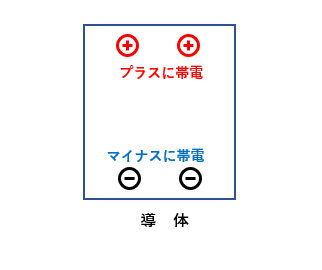
図のように 帯電していない導体があります。

マイナスの帯電体を、帯電していない導体に近づけます。
帯電体のマイナスと導体のマイナスが反発して、電子が下へ移動します。

導体の上側がプラスに、下側がマイナスに帯電します。
電荷がゼロの意味
物質が摩擦などにより電気を帯びることを 帯電 といいます。
帯電は電子の移動によって起こります。
帯電したもの同士の間には クーロン力 が働きます。
クーロン力の向きは
同じ種類の電気の場合は 斥力 が働き
異なる電気の場合は 吸引力 が働きます。
■ 電荷ゼロの意味すること
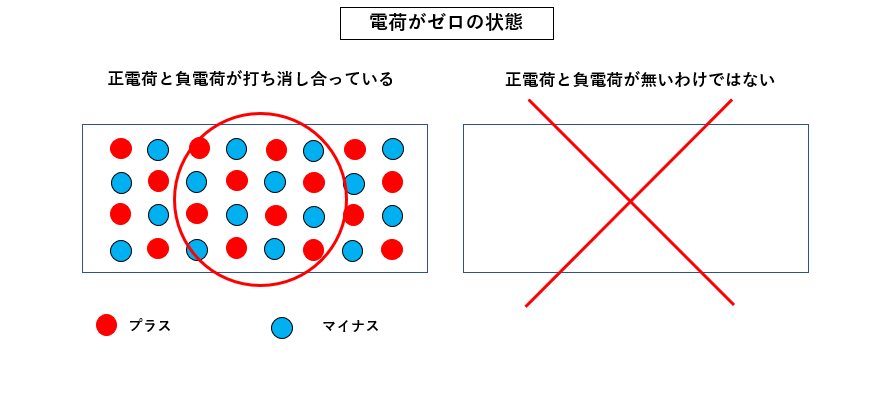
電気を帯びていない状態のときを、一般的に 電荷がゼロ と表現します。
電荷がゼロというと、まるで 電荷が無い というように思ってしまいます。
しかし、電荷がゼロという状態は 図のようにプラスとマイナスの数が一致していて電気的に中性の状態のことをいいます。
決して電荷がないわけではありません。
帯電する仕組み
導体がプラスに帯電したり、マイナスに帯電するのは、原子の中の 自由電子 が移動するからです。
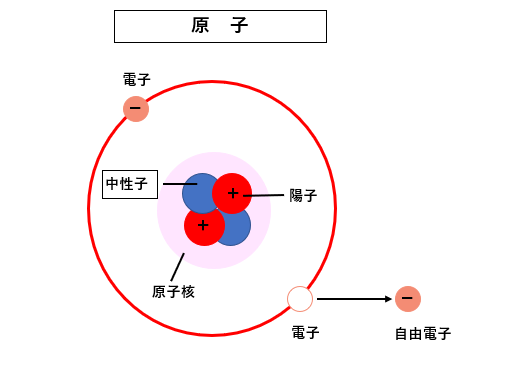
プラスに帯電する
外から何らかの刺激を受けて電子が飛び出すと、図のように プラス に帯電することになります。
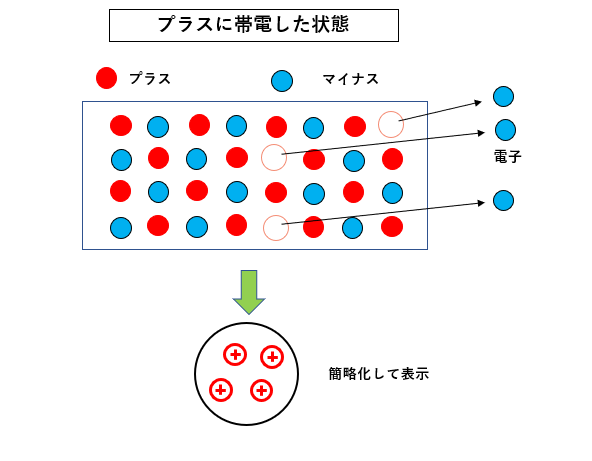
プラスに帯電したということは、電子が抜けたことで相対的にプラスになったということであり
決してマイナスの要素がなくなったわけではない。
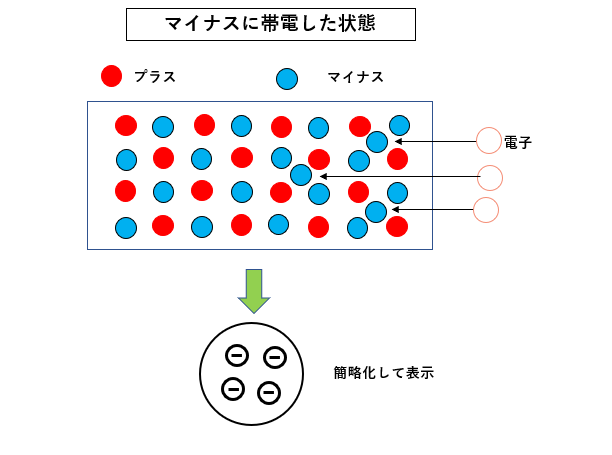
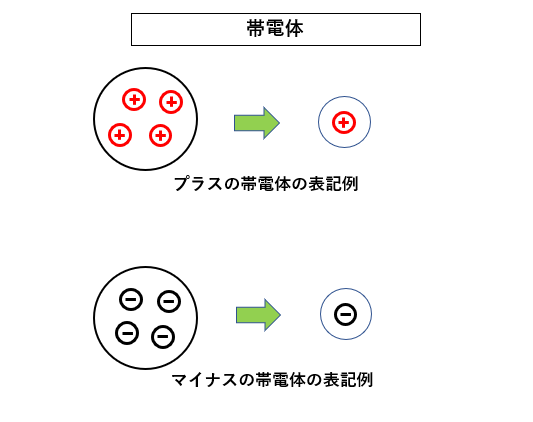
■ 帯電の状態
電気では電荷がプラスやマイナスに帯電しているというときに、図のように単純化して表示します。
図のような表示を見るとプラスの帯電体にはプラスの電荷だけがあり、マイナスの帯電体にはマイナスの電荷だけがあるように勘違いしてしまいます。
■ 帯電列
帯電の目安として「帯電列」というものがあります。

例えば、ガラス棒を布でこするとガラス棒から布へ電子が移動するので、ガラス棒はプラスに帯電し、布はマイナスに帯電します。
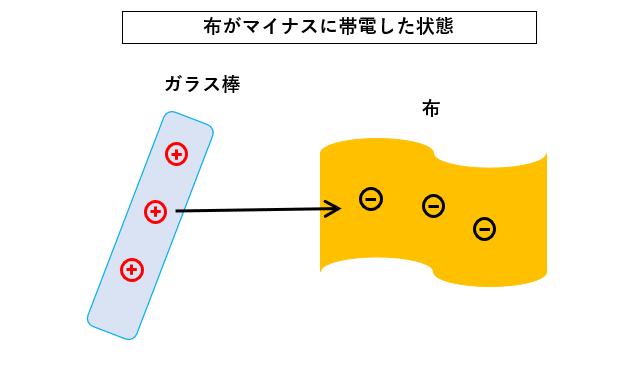
物質が帯電する現象は 静電誘導 によるものです。
例題1
3つの帯電体A、B、C があります。
- AとBを近づけると互いに引き合いました。
- AとCを近づけると互いに反発しました。
BとCを近づけると斥力と引力のどちらの力が働くでしょう。
<解答例>
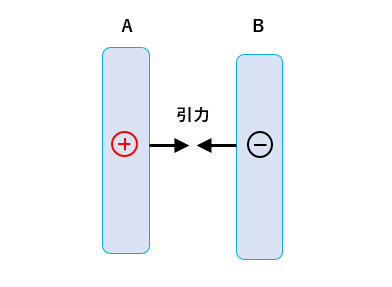
AとBを近づけたとき引き合ったので、AとBは異種の電荷になります。
Aをプラスとすれば、Bはマイナスに帯電しています。
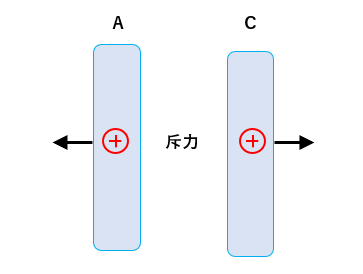
AとCを近づけると反発したので、AとCは同種の電荷になります。
Aがプラスなので、Cもプラスに帯電しています。
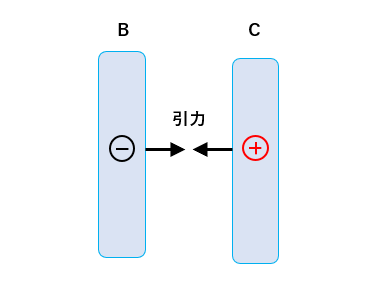
Bはマイナスに帯電し、Cはプラスに帯電しているので互いに近づけると引力が働きます。
重力による位置エネルギー
位置エネルギーとは物体がある高さにあるとき、その物体が高さを持つということだけでエネルギーを持っています。
このエネルギーのことを位置エネルギーといいます。
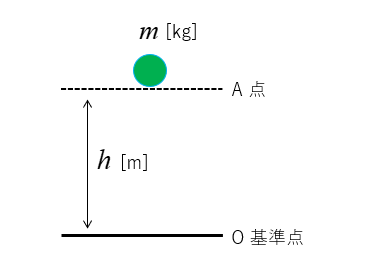
図において \(m\) [kg] の物体が高さ \(h\) [m] にあるときの位置エネルギー \(U_g\) は重力加速度を \(g=9.8\) [m/s2] とすると
重力による位置エネルギーは
\(U_g=mgh\) [J] になります。
力 = 質量 × 加速度
\(F(N)=m(kg)×g(m/s^2)\)
仕事 = 力 × 距離
\(W(J)=F(N)×d(m)\)
単位 \(J=N\cdot m\)
保存力について
保存力には重力や静電気力、弾性力があります。
これに対し非保存力には摩擦力や空気抵抗などがあります。
保存力とは、物体を A から B まで運ぶ「力がする仕事」が物体を運ぶ経路(道筋)に関係なくスタートとゴールの位置だけで決まる場合の力のことです。
図のように物体をAからBまで、斜面を運ぶ場合とP点を経由して運ぶ場合を考えます。
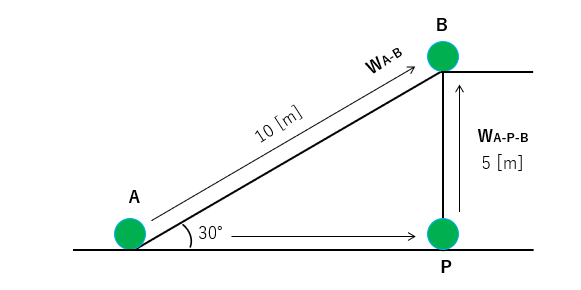
物体の質量 \(m\) を 1 [kg] 、斜面の距離 \(d\) を 10 [m] 、重力加速度 \(g\) を 9.8 [m/s2] とします。
■ AからBまでのなめらかな斜線を運ぶ仕事 \(W_{A-B}\) を考えます。
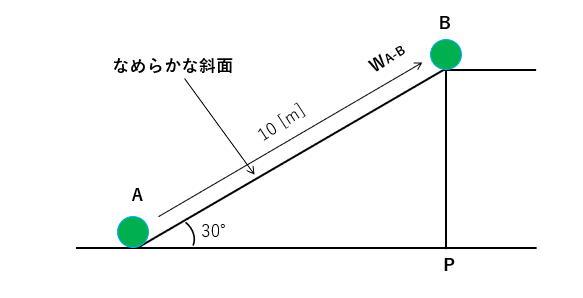
物体 \(m\) にかかる重力は斜面に水平方向の力 \(F_L\) と垂直方向の力 \(F_V\) に分けることができます。
物体を引き上げるために必要な力は 斜面に水平方向の力 \(F_L\) になります。
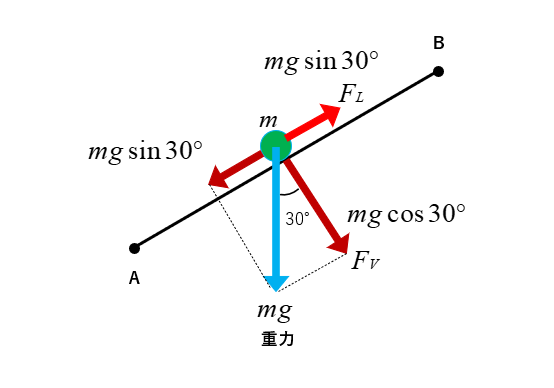
斜面をAからBまで引き上げる仕事 \(W_{A-B}\) は仕事=力×距離 ですから
\(W_{A-B}=F_L×d\)
\(W_{A-B}=\cfrac{1}{2}×9.8×10=49\) [J] \(\cdots(1) \) になります。
■ AからPを経由してBまで運ぶ仕事を \(W_{A-P-B}\) を考えます。
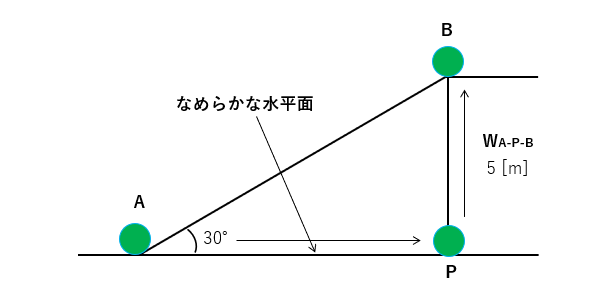
なめらかな水平面をAからPまで移動する力 \(F_L\) は ゼロ になります。
\(F_L=mg\sin0=0\) なので
なめらかな水平面をAからPまで移動する仕事 \(W_{A-P}\) は ゼロ になります。
\(W_{A-P}=0\)
PからBまで移動する仕事 \(W_{P-B}\) は
\(W_{P-B}=mgd=1×9.8×5=49\) [J] になり、式(1)と等しくなります。
このように \(W_{A-B}\) の仕事と \(W_{A-P-B}\) の仕事が等しいとき、物体に働いている力を 「保存力」 といいます。
位置エネルギーの計算方法”>物体が基準点まで移動するときにする仕事が保存力になります。物体が持つ位置エネルギーを計算するには、保存力がする仕事を計算することで求められます。
以上で「静電容量・静電誘導・帯電の仕組み・保存力について」の説明を終わります。