点電荷が作る電界の強さは、電荷の大きさに比例し、距離の2乗に反比例します。
点電荷から r [m] の位置の電界の強さは等電位面になります。
等電位面は r [m] の球体の位置の電界の強さになります。
2つの点電荷の間に働く力について説明します。
点電荷が作る電界の強さ
点電荷 \(Q\) [C] から \(r\) [m] 離れた位置を 点 \(P\) とします。
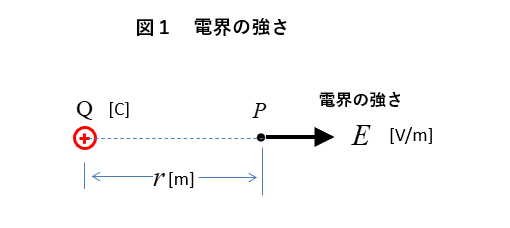
点電荷 \(Q\) [C] が
点 \(P\) に作る 電界の強さ \(E\) [V/m] は 次の式で表されます。
\(E=k\cfrac{Q}{r^2}=\cfrac{Q}{4πε_0r^2}\) [V/m]
\(E=9×10^9×\cfrac{Q}{r^2}\) [V/m]
電界の強さ
電界の強さは誘電率 \(ε\) の媒質中では次の公式になります。
\(E=k\cfrac{Q}{ε_rr^2}=\cfrac{Q}{4πε_0ε_rr^2}\) [V/m]
誘電率は電荷の貯めやすさの比率を表します。
\(k=\cfrac{1}{4\piε_0}=9×10^9\) [N・m2/C2]\(\cdots\)定数
\(ε_0=8.854×10^{-12}\) [F/m]\(\cdots\)真空の誘電率
\(ε=ε_0ε_r\) [F/m]\(\cdots\)誘電率で「イプシロン」と読みます。
\(ε_r=\cfrac{ε}{ε_0}\)\(\cdots\)比誘電率 空気中では \(ε_r=1\) です。
\(k=\cfrac{1}{4\piε}\cdots\)誘電率εの媒質中の定数
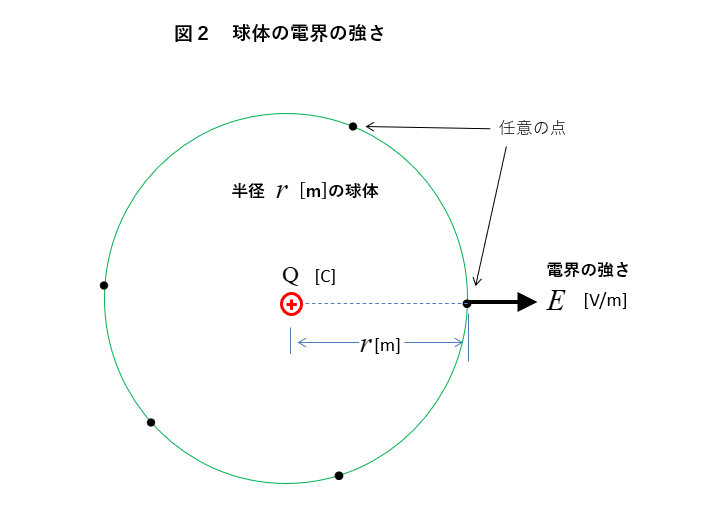
球体の電界の強さ
電界の強さは 点電荷から半径 \(r\) [m] の球体を考えると
球体から半径 \(r\) [m] の 任意の点 の電界の強さ \(E\) はどこでも同じになります。
★ 電界の強さの単位は、一般的に [V/m] が使用されますが
次のように単位を変換することが出来るますので [V/m] と {N/C] は等しくなります。
■ 単位の変換
\(\rm N=\cfrac{J}{m}\)
\(\rm V=\cfrac{J}{C}\)
\(\rm \cfrac{V}{m}=\cfrac{J}{C・m}=\cfrac{N}{C}\)
2つの点電荷間に働く力
クーロンの法則
★ 点電荷間に働く力は クーロンの法則 により求められます。
\(F=k\cdot\cfrac{Q_1Q_2}{r^2}\) [N]
\(F=9×10^9×\cdot\cfrac{Q_1Q_2}{r^2}\) [N]
★ クーロンの法則は誘電率 \(ε\) の媒質中では次の公式になります。
\(F=k\cdot\cfrac{Q_1Q_2}{ε_rr^2}\) [N]
誘電率は電荷の貯めやすさの比率を表します。
\(k=\cfrac{1}{4\piε_0}=9×10^9\) [N・m2/C2]\(\cdots\)定数
\(ε_0=8.854×10^{-12}\) [F/m]\(\cdots\)真空の誘電率
\(ε=ε_0ε_r\) [F/m]\(\cdots\)誘電率で「イプシロン」と読みます。
\(ε_r=\cfrac{ε}{ε_0}\)\(\cdots\)比誘電率 空気中では \(ε_r=1\) です。
\(k=\cfrac{1}{4\piε}\cdots\)誘電率εの媒質中の定数
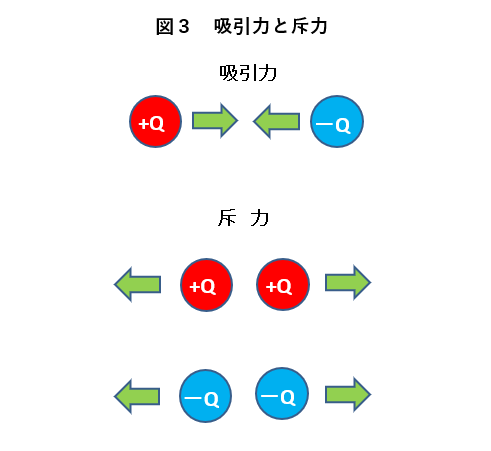
電荷間に働く力の方向
異種の電荷間には 吸引力 が働き
同種の電荷間には 斥力 が働きます。
平等電界中の電荷が受ける力
平等電界中 \(E\) [V/m] にある電荷 \(q\) [C] が
受けるクーロン力(静電気力)\(F\) [N] は
\(F=qE\) [N]
以上で「点電荷が作る電界の強さと点電荷に働く力」の説明を終わります。