電気力線と電気力線密度

電界　は目に見えないので、理解しづらいものです。

そこで、電界の様子を表すための　仮想的な線　が考えられました。

それが　電気力線　です。

電気力線と同じように、電界の様子を見るための仮想的な線として　電束　があります。

電気力線の形状や電気力線の本数などについて説明します。

電気力線の形状

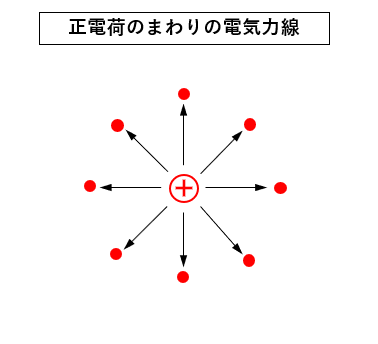
正電荷　からは、図のように電気力線が出ている様子を表しています。

正電荷の周りに　プラスの点電荷　を置いたとすれば

プラス同士なので　斥力　が働きますので矢印のような向きになることがわかります。

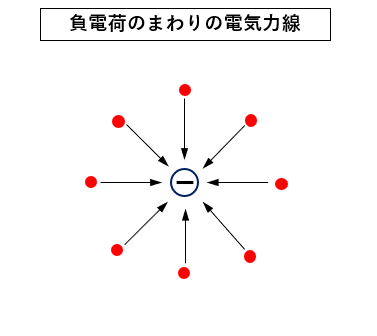
負電荷　には、図のように電気力線が入り込む様子を表しています。

負電荷の周りに　プラスの点電荷　を置いたとすれば

異なる電荷なので　引力　が働きますので矢印のような向きになることがわかります。

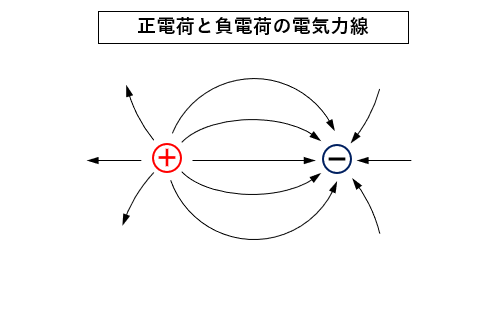
正電荷と負電荷の電気力線

正電荷　と　負電荷　が近くにある場合

電気力線は正電荷から出発して、負電荷に入る様子を示しています。

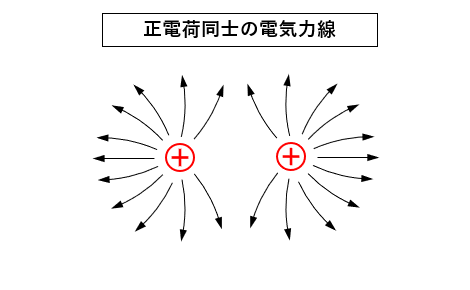
正電荷同士　が近くにある場合、互いに反発する様子を示しています。

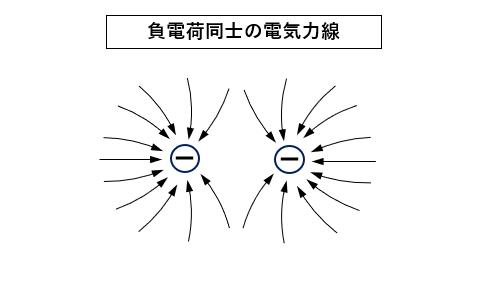
負電荷同士　が近くにある場合、互いに反発する様子を示しています。

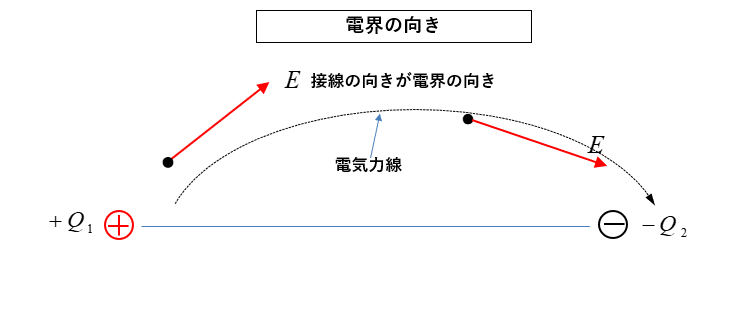
電界の向き

図のように、電気力線の接線の向きが電界の向きになる。

等電位面

等電位面とは電位の等しい面のことをいいます。

図のように　点電荷から　\(ｒ\)　[m]　の電位は

\(V=k\cfrac{Q}{r}\)　[V]　になります。

等電位面を平面で見れば　図のような円になります。

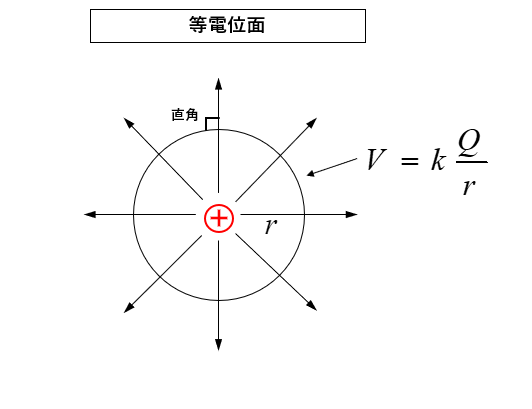
点電荷からは球面上に電気力線が出ていますので、等電位面は球面になります。

電気力線は等電位面に対して　直角　に貫いている。

電気力線の本数

図のように、電界の強さ　\(E\)　の面において

単位面積当たり　\(E\)　本　の電気力線が直角に貫くと決めます。

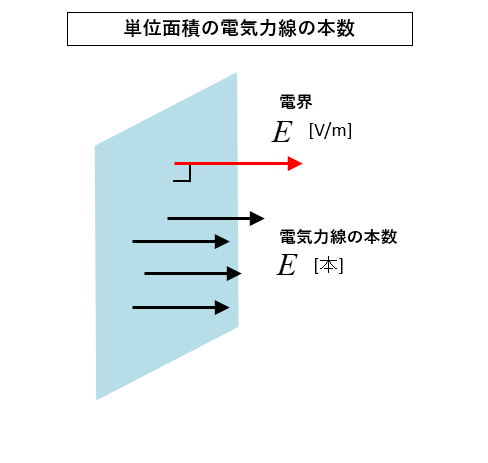
電気力線の本数

電荷　\(Q\)　から出る電気力線の総本数　\(N\)　は　次のようになります。

\(N=4πkQ\)　[本]　

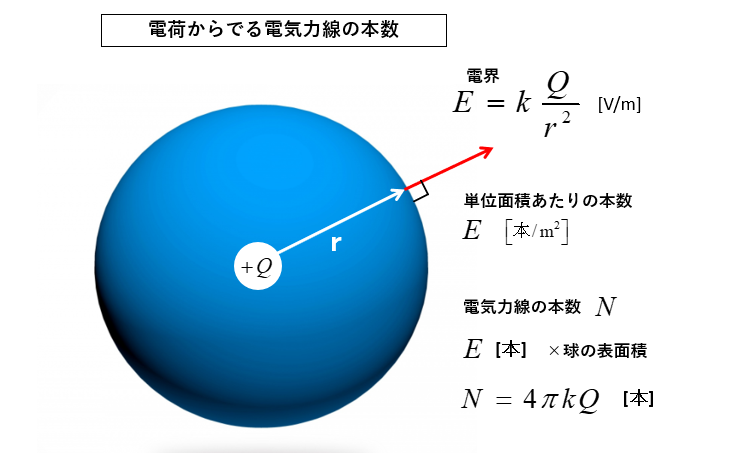
図において

電荷　\(Q\)　から　\(ｒ\)　の電界の強さは

\(E=k\cfrac{Q}{r^2}\)　です。

単位面積あたりの電気力線の本数は

\(E\)　[本/m²]　なので

電気力線の総本数　\(N\)　は、球の表面積を掛ければ求められます。

\(N=E×4πr^2=4πkQ\)　[本]　\(\cdots (1)\)

定数　\(k\)　は

\(k=\cfrac{1}{4πε}\)　\(\cdots (2)\)

式（２）を　式（１）へ代入すると

\(N=\cfrac{Q}{ε}\)　[本]　になります。

電気力線密度

電荷　\(Q\)　からは　\(N=4πkQ\)　[本]　の電気力線が出ています。

電気力線密度　[本/m²]　は単位面積あたりの電気力線の本数です。

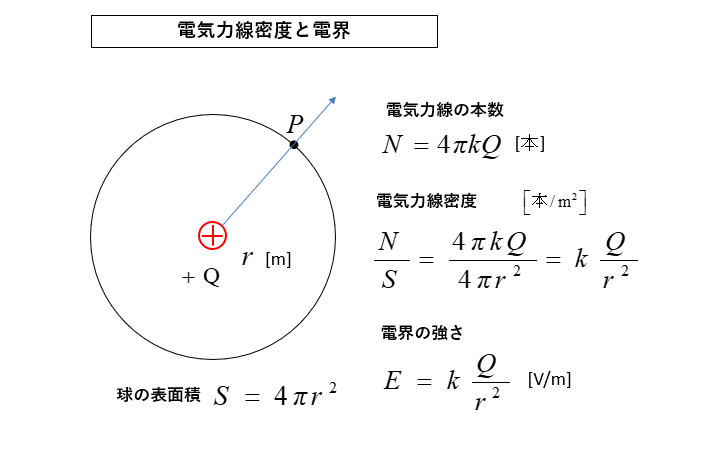
電気力線の定義から　単位面積あたりの電気力線の本数は電界の強さです。

電気力線密度　[本/m²]　＝　電界の強さ　[V/m]　になります。

電気力線の総数を球の面積　\(4πr^2\)　で割ると　電界の強さ　になります。

電気力線密度\(=\cfrac{1}{4πr^2}×\cfrac{Q}{ε}\)\(=\cfrac{Q}{4πεr^2}=\)電界の強さ \(E\)　になります。

ガウスの法則

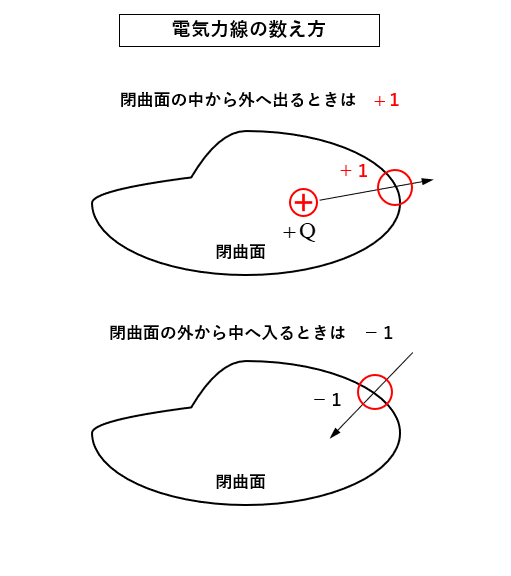
■　電気力線の数え方

図のように　電気力線が閉曲面の中から外へ出るときは＋１と数えます。

電気力線が閉曲面の外から中へ入るときは－１と数えます。

ガウスの法則

図のように、閉曲面の外にある電荷　\(+q\)　が

電気力線が閉曲面を貫いても相殺されて閉曲面の内部に影響を与えません。

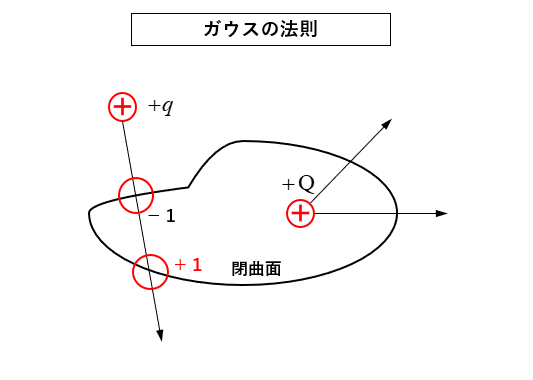
★　閉曲面の内部にある電荷から出る電気力線は　

内部にある電荷によって決まり　外部の電荷の影響は無視できるということです。

以上で「電気力線と電気力線密度」の説明を終わります。