交流回路においてリアクタンスは、 電源からの電力を受け取ったり、電源に戻したりするので電力を消費しないことになります。
誘導リアクタンス回路は電力を消費しない
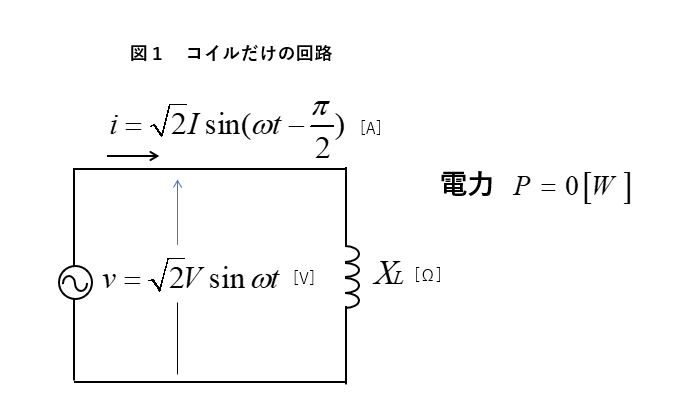
■ 図1のように、コイルだけの回路に、交流電圧を加えます。
誘導リアクタンス を \(X_L\) 電圧の 実効値 を \(V\) とします。
コイルだけの回路には 電流の位相が電圧より \(\cfrac{π}{2}\) 遅れた電流 \(i\) (実効値 \(I\))が流れます。
★ 電圧 \(v\) と電流 \(i\) の瞬時値は、次のとおりです。
\(v=\sqrt2 V\sinωt\) [V]
\(i=\sqrt2 I\sin(ωt-\cfrac{π}{2})\) [A]
瞬時値電力 \(p\) は、次のようになります。
\(p=vi\)\(=\sqrt2 V\sinωt×\sqrt2 I\sin(ωt-\cfrac{π}{2})\)\(=-2VI\sinωt\cosωt\)
\(p=-VI\sin2ωt\)\(\cdots(1)\)
式(1)で \(\sinωt\) を1周期で平均すると 0(ゼロ) になりますので
誘導リアクタンス回路の電力 \(p\) は \(p=0\) になります。
■ 三角関数
\(\sin(ωt-\cfrac{π}{2})=-\cosωt\)
\(2\sinωt\cosωt=\sin2ωt\)
★ 電圧、電流、電力の関係は 図2のようになります。
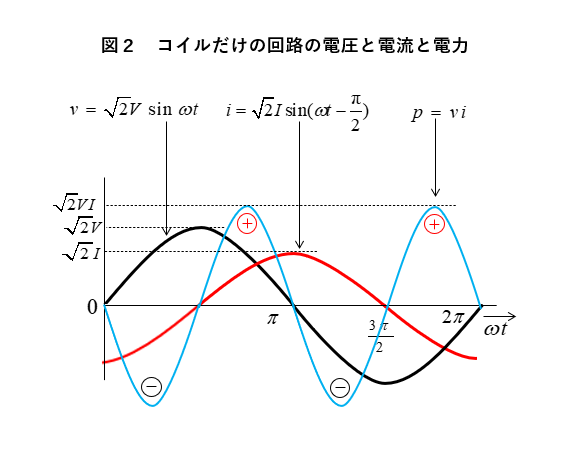
★ 誘導リアクタンス \(X_L\) の瞬時電力 \(p\) において
\(p\) が(+)の期間では、電源からの電力は誘導リアクタンス \(X_L\) に 電磁エネルギー として蓄えられます。
\(p\) が(ー)の期間では、誘導リアクタンス \(X_L\) に蓄えられていた 電磁エネルギー が電源に還流されます。
誘導リアクタンス回路では電力を消費しないことになります。
容量リアクタンス回路は電力を消費しない
誘導リアクタンスと同じように、容量リアクタンス回路でも電力を消費しません。
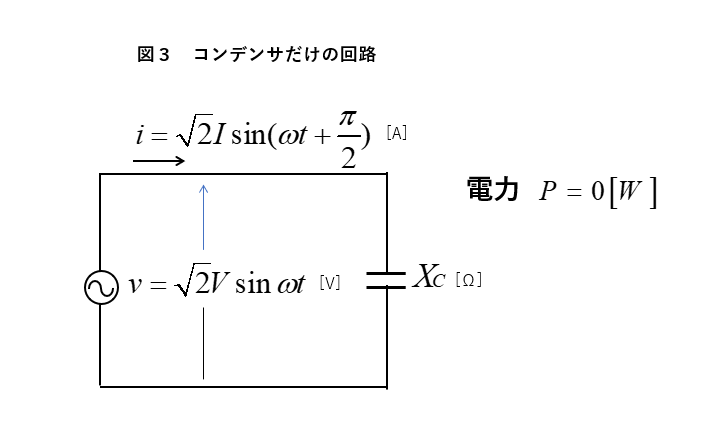
★ 図3のように、コンデンサだけの回路に、交流電圧を加えます。
容量リアクタンス を \(X_C\) 電圧の 実効値 を \(V\) とします。
コンデンサだけの回路には、電流の位相が電圧より \(\cfrac{π}{2}\) 進んだ電流 \(i\)(実効値 \(I\)) が流れます。
★ 電圧 \(v\) と電流 \(i\) の瞬時値は、次のとおりです。
\(v=\sqrt2 V\sinωt\) [V]
\(i=\sqrt2 I\sin(ωt+\cfrac{π}{2})\) [A]
瞬時値電力 \(p\) は、次のようになります。
\(p=vi\)\(=\sqrt2 V\sinωt×\sqrt2 I\sin(ωt+\cfrac{π}{2})\)\(=2VI\sinωt\cosωt\)
\(p=VI\sin2ωt\)\(\cdots(2)\)
式(2)で \(\sinωt\) を1周期で平均すると 0(ゼロ) になりますので、容量リアクタンス回路の電力 \(p\) は \(p=0\) になります。
■ 三角関数
\(\sin(ωt+\cfrac{π}{2})\)\(=\cosωt\)
\(2\sinωt\cosωt=\sin2ωt\)
★ 電圧、電流、電力の関係は 図4のようになります。

★ 容量リアクタンス \(X_C\) の瞬時電力 \(p\) において
\(p\) が(+)の期間では、電源からの電力は容量リアクタンス \(X_C\) に 静電エネルギー として蓄えられます。
\(p\) が(ー)の期間では、容量リアクタンス \(X_C\) に蓄えられていた 静電エネルギー が電源に還流されます。
容量リアクタンス回路では電力を消費しないことになります。
つまり、リアクタンスは、誘導リアクタンスも容量リアクタンスも電力を消費しないことがわかります。
以上で「リアクタンス回路は電力を消費しない」の説明を終わります。