交流回路の電力には、皮相電力・有効電力・無効電力の3つがあります。
皮相電力:皮相電力は電源から送られる電力のことです。
有効電力:有効電力は送られた電力の中で、実際に負荷で消費される電力のことです。
無効電力:無効電力は送られた電力の中で、消費されずに電源に返される電力のことです。
ここでは、皮相電力・有効電力・無効電力の関係について説明します。
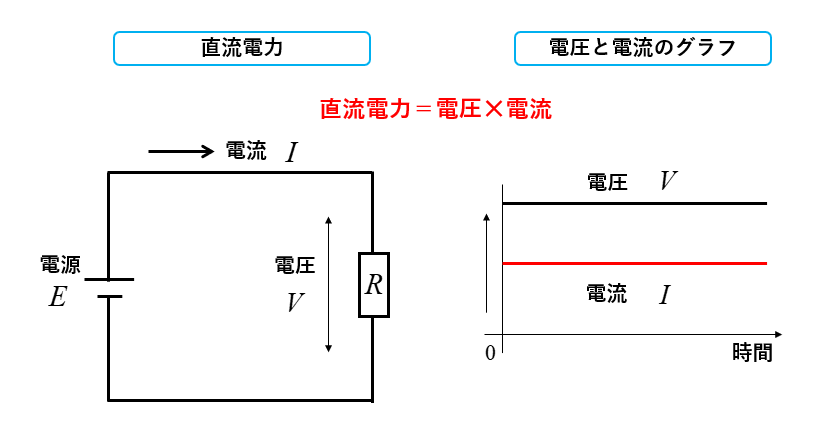
直流電力と交流電力の違い

直流電力は、単に電圧と電流を掛け算すれば求められます。
直流は時間が経過しても、電圧と電流の大きさは変わらないため、直流の電力は、直流電力=電圧✕電流 [W] で求められます。
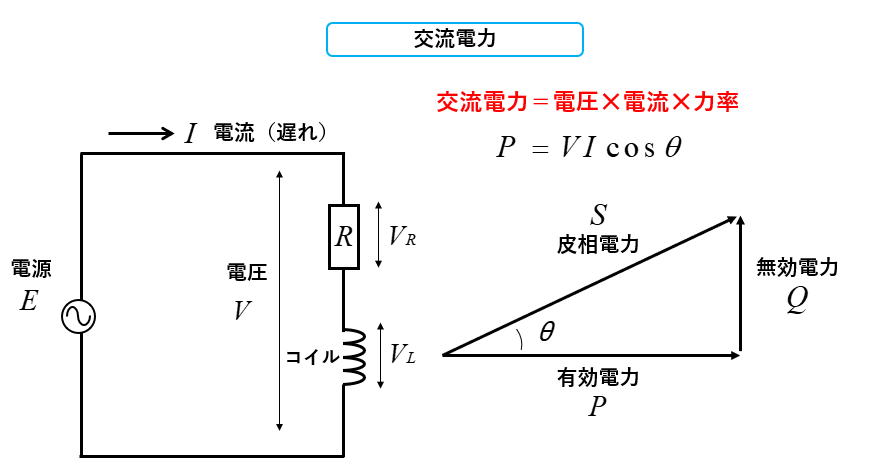
負荷が抵抗とコイルの回路の交流電力は、交流電力=電圧✕電流✕力率 [W] になります。
単に交流電力という場合は、有効電力を示します。
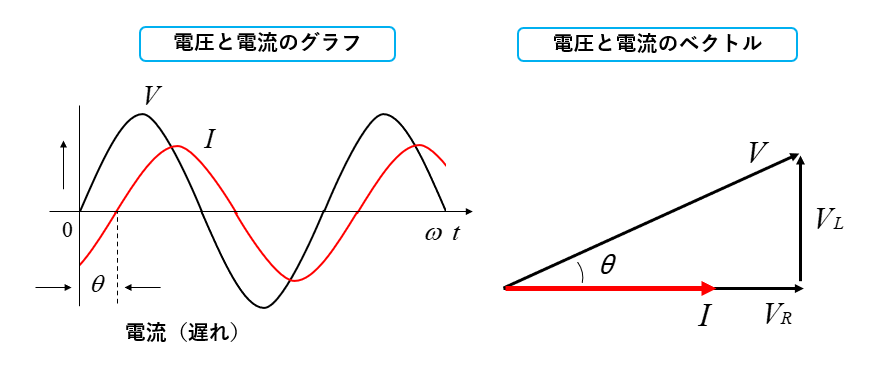
電圧と電流のグラフとベクトル
抵抗とコイルの回路では、電流の位相が電圧より遅れる。
皮相電力:\(S=VI\) [VA](ボルトアンペア)
有効電力:\(P=VI\cosθ\) [W](ワット)
無効電力:\(Q=VI\sinθ\) [var](バール)
力率については次の記事が参考になります。

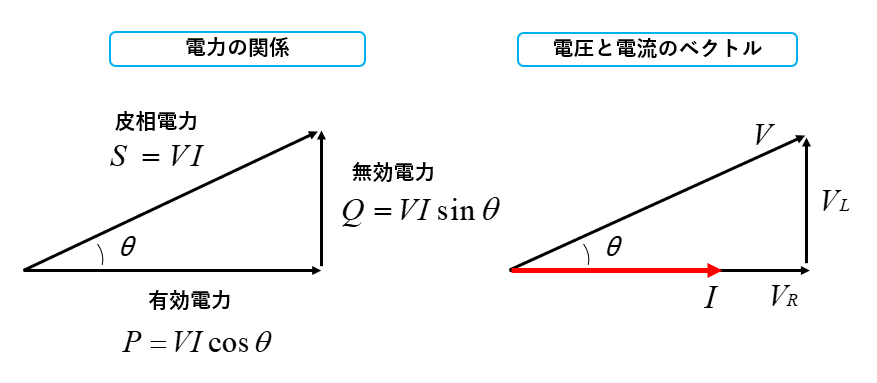
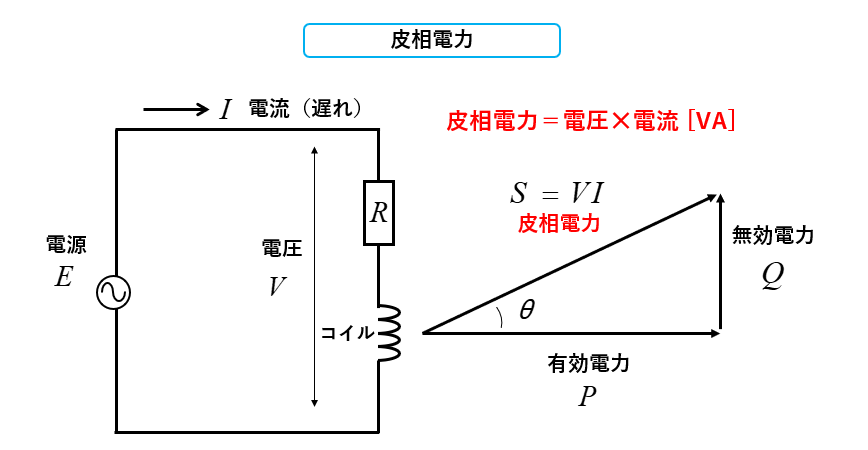
皮相電力
皮相電力は、負荷に供給された電力のことで、電圧と電流の積になります。
皮相電力=電圧✕電流で \(S=VI\) [VA](ボルトアンペア)
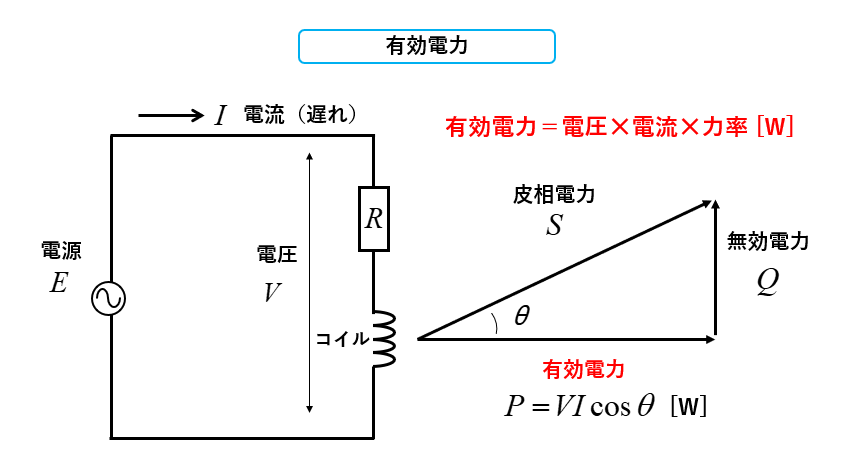
有効電力
有効電力は、供給された電力の中で実際に消費された電力になります。
有効電力=電圧✕電流✕力率で \(p=VI\cosθ\) [W](ワット)
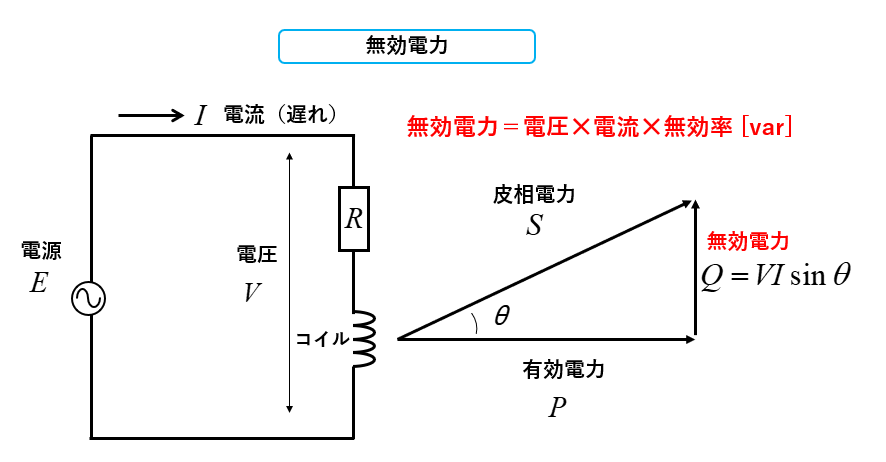
無効電力
無効電力は、供給された電力の中で消費されずに電源に戻ります。
無効電力=電圧✕電流✕無効率で \(Q=VI\sinθ\) [var](バール)

まとめ
皮相電力・有効電力・無効電力と力率の関係は、図のように電力の三角形で表すことができます。

| 公 式 | 単 位 | |
| 皮相電力 | \(S=VI\) | [VA](ボルトアンペア) |
| 有効電力 | \(P=VI\cosθ\) | [W](ワット) |
| 無効電力 | \(Q=VI\sinθ\) | [var](バール) |
以上で「皮相電力・有効電力・無効電力の関係をやさしく解説!」の説明を終わります。