この記事では
- 電界(電場)とは何のこと?
- 電界を求める公式
- 電界の中で働く力(クーロン力)
について説明しています。
電荷による 静電気力(クーロン力)が働く空間 のことを 電界(または電場)といいます。
電界の強さは+1C(クーロン)の電荷が受ける静電気力と定められています。
ここでは、電荷から距離 \(r\) [m] の位置の電界の強さを求める公式、電界のベクトル合成、電界中にある電荷に働く力を説明します。
電界とは
プラスチックの下敷きを「こすったり」すると電気を帯びて、髪の毛や糸くずなどを引きつけるような状態になります。
目には見えませんが 何かが作用 しています。
物質が何らかの方法で、電気を帯びた状態を 帯電 しているといい、帯電している物質を 帯電体 といいます。
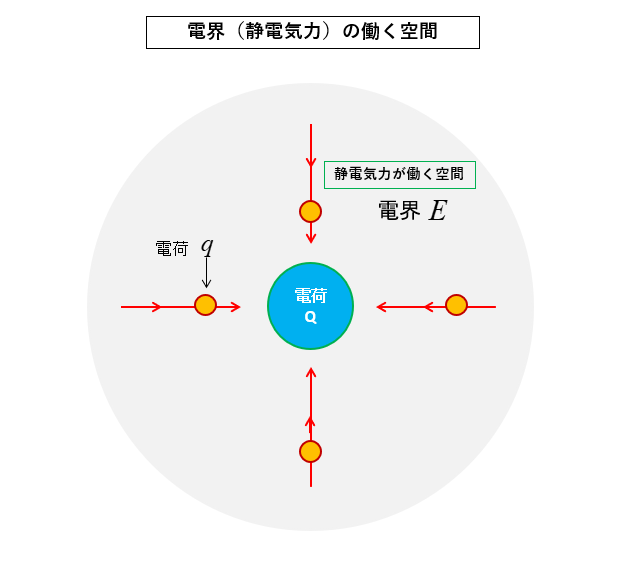
目には見えませんが、帯電体の周りには何かの力が働いています。
この力を 静電気力(クーロン力)といい
図のように静電気力(クーロン力)が、働く空間のことを 電界(または電場)といいます。
吸引力と斥力
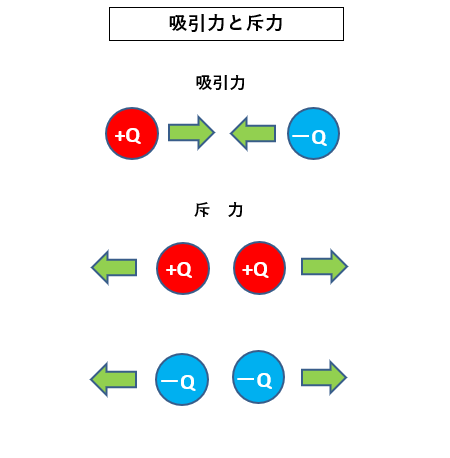
- 図のように 正電荷 と 負電荷 のように、異なる電荷の間には 吸引力 が働きます。
- 正電荷同士 または 負電荷同士 のように同じ電荷の間には斥力が働きます。
電界の強さ
電界の強さの公式
図のように 真空中に点電荷 \(Q\) [C] を置きます。

電界の強さ \(E\) [V/m] は
点電荷から \(r\) [m] の点に +1C(クーロン)の電荷を置いたときに
この電荷が受ける 力の大きさと方向 で表します。
クーロンの法則の公式
2つの電荷間に働く静電気力は クーロンの法則 で求めることができます。
\(F=k\cfrac{Q_1Q_2}{r^2}\) [N]
+1C(クーロン)の電荷が受ける静電気力が電界の強さ \(E\) なので
\(E=k\cfrac{Q}{r^2}\) [V/m] = [N/C]
■ 単位の変換
\(N=\rm\cfrac{J}{m}\)
\(V=\rm\cfrac{J}{C}\)
\(\rm\cfrac{V}{m}=\cfrac{J}{C\cdot m}=\cfrac{N}{C}\)
- 誘電率は電荷の貯めやすさの比率を表します。
- \(k=\cfrac{1}{4\piε_0}=9×10^9\) [N・m2/C2]\(\cdots\)定数
- \(ε_0=8.854×10^{-12}\) [F/m]\(\cdots\)真空の誘電率
- \(ε=ε_0ε_r\) [F/m]\(\cdots\)誘電率で「イプシロン」と読みます。
- \(ε_r=\cfrac{ε}{ε_0}\)\(\cdots\)比誘電率 空気中では \(ε_r=1\) です。
- \(k=\cfrac{1}{4\piε}\cdots\)誘電率εの媒質中の定数
電界の中にある電荷に働く力
電界の強さが \(E\) の点における電荷 \(q\) に働く力 \(F\) は 次のようになります。
\(F=qE\) [N]
静電気力の求め方
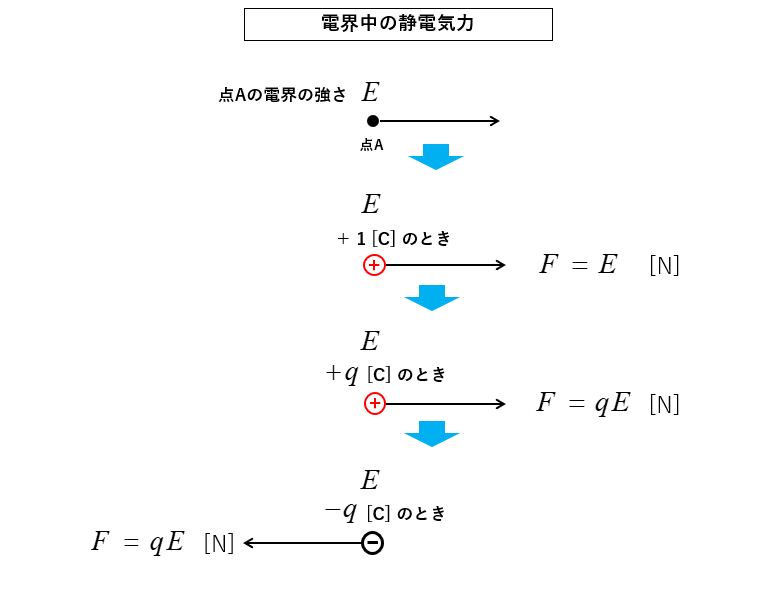
- 点Aの電界が \(E\) の時 +1 [C] の電荷が受ける力 \(F\) は右向きで大きさは \(F=E\) [N] になります。
- 点Aの \(+q\) [C] の電荷が受ける力 \(F\) は 右向き で大きさは \(F=qE\) [N] になります。
- 点Aの \(-q\) [C] の電荷が受ける力 \(F\) は 左向き で大きさは \(F=qE\) [N] になります。
電界の合成
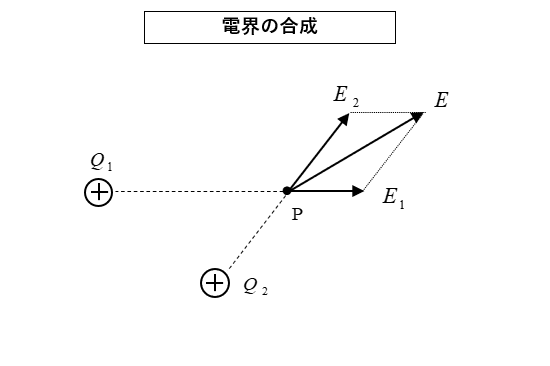
複数の点電荷による P点の電界の強さは
各点電荷によって作られる 電界のベクトル和 として求めることができます。
電界の公式
電界の強さ \(E\) [V/m] は次のようになります。
\(E=k\cfrac{Q}{r^2}\) [V/m]
\(E=9×10^9\cfrac{Q}{r^2}\) [V/m]
誘電率 \(ε\) の媒質中では、次の公式になります。
\(E=k\cfrac{Q}{ε_rr^2}\) [V/m]
電界の強さが \(E\) の点における電荷 \(q\) に働く力 \(F\)
\(F=qE\) [N]
練習問題
問題1
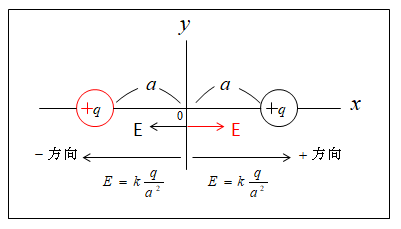
★ 図の中心 0 での電界を求めよ。
<解答例>
中心 0 での電界を求める。
左の \(+q\) が中心 0 に作る電界は、電界の強さの公式から \(E=k\cfrac{Q}{r^2}\) になります。
\(E=k\cfrac{q}{a^2}\)
右の \(+q\) が中心 0 に作る電界も同じく
\(E=k\cfrac{q}{a^2}\)
電界はベクトルの和になるので、0 になります。
\(k\cfrac{q}{a^2}+(-k\cfrac{q}{a^2})=0\)
問題2
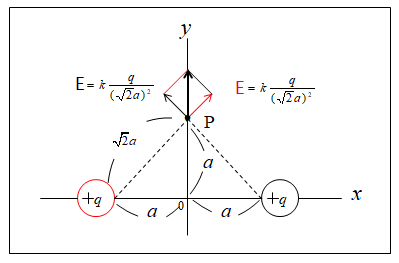
★ y軸上の P点の電界の強さの合計を求めよ。
<解答例>
y軸上の P点の電界の強さの合計を求める。
y軸上の P点の電界の強さ \(E\) は共に
\(E=k\cfrac{q}{(\sqrt2a)^2}\)
P点の電界の合計はベクトル和になりますので、\(\sqrt2E\) になります。
\(\sqrt2E=kq×\cfrac{\sqrt2}{2a^2}\)
以上で「電界の強さ」の説明を終わります。