発電所で作られた電気は交流電力で送られています。
一般家庭に送られてくるまでには、変圧器で送電や配電の途中で電圧を上げたり下げたりしています。
交流の電圧を昇圧したり、降圧したりするための電気機器が 変圧器 というものです。
「強電」で使われている変圧器は、電柱の上にある柱上変圧器などがあります。
柱上変圧器は6000Vなどの高圧を、家庭で使うような100Vや200Vに変圧しています。
ここでは、変圧器の原理について説明します。
変圧器の原理は相互誘導
図は 電磁誘導 により、コイルに誘導電流が発生する仕組みを表しています。
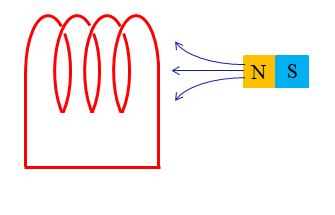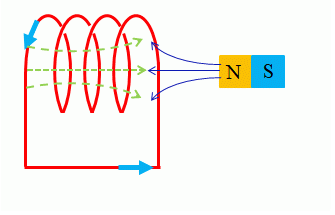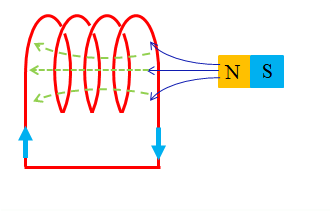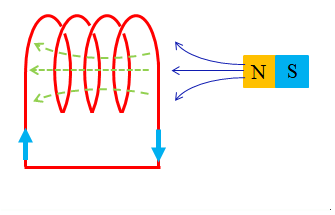
磁石を出し入れすることにより、コイルが受ける磁界の強さが変化しています。
この磁界の強さが変化することにより、コイルに 電磁誘導 による起電力が発生します。
ここで、変圧器を考えて見ましょう。
電磁誘導の説明図になります。
変圧器の原理図になります。
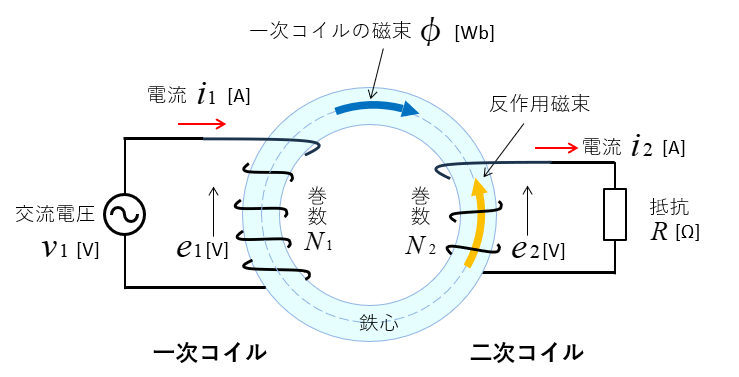
上の２つの図を比較すると、次のようになります。
- 電磁誘導の説明図の、磁石の出し入れによる磁界の変化を、変圧器の一次コイルの変化と見ることができます。
- 電磁誘導の説明図の、誘導起電力が発生するコイルを、変圧器の二次コイルと見ることができます。
- 変圧器では一次コイルを交流電源に接続することで、磁界の大きさが変化します。
この現象は電磁誘導の説明図の、磁石の出し入れによる磁界の変化と同じことになります。
■ 相互誘導
相互誘導 とは一次コイルの磁界を変化させることにより、電源を持たない二次コイルに起電力が発生する現象のことをいいます。
変圧器の原理 は、相互誘導を利用したものです。
変圧器の説明
変圧器は相互誘導により、二次側のコイルに起電力を発生することができます。
二次コイルに発生する誘導起電力の大きさは、二次コイルの巻数に比例します。
つまり、二次コイルの巻き数を変えることにより、取り出す電圧の大きさを自由に調整できることになります。
これが 変圧器 が電圧を上げたり、下げたりできる原理です。
上の図で説明すると
一次コイルの巻数を \(N_1\)、二次コイルの巻数 \(N_2\) とした場合
一次コイルに \(E_1\) の電圧を加えると、二次コイルに \(E_2\) の電圧が発生します。
電圧 \(E_1、E_2\) の大きさは、一次コイル、二次コイルそれぞれの巻数に 比例 します。
\(\cfrac{E_1}{E_2}=\cfrac{N_1}{N_2}\)
\(E_2=\cfrac{N_2}{N_1}E_1\)
電流 \(I_1、I_2\) の大きさは、一次コイル、二次コイルそれぞれの巻数に 反比例 します。
\(\cfrac{I_1}{I_2}=\cfrac{N_2}{N_1}\)
\(I_2=\cfrac{N_1}{N_2}I_1\)
ただし、電力は一定ですから、次の式が成立します。
\(\cfrac{E_1}{E_2}\)\(=\cfrac{N_1}{N_2}\)\(=\cfrac{I_2}{I_1}\)
\(E_1I_1=E_2I_2\quad\rm[VA]\)
変圧器の使用電圧と電流は決まっていて、二次コイル側の両者の積を 変圧器の定格容量 といいます。
実際の変圧器は内部にわずかながらの損失があります。
変圧器の鉄心を成層鉄心で作る理由
変圧器は磁束の変化で誘導起電力を発生させて利用していますが、実は 渦電流 が鉄心にも流れてしまいます。
これが熱になって損失になります。
とくに電力系の変圧器では、渦（うず）電流損による発熱ロスが大きくなってしまいます。
そこで、このうず電流を少なくするために、鉄心を薄く切ってそれぞれの境を絶縁して抵抗を大きくして、
成層鉄心にする事で損失を小さくしています。
渦電流は磁束と垂直の方向、つまり鉄心の断面方向に発生します。
そのため、薄い鉄板を何枚も重ねた成層鉄心にすることで、渦電流を抑えるようにしています。
以上で「変圧器の原理」の説明を終わります。