コンデンサに電流を流すと、コンデンサには電気エネルギーが貯まります。
また、コンデンサに流れる電流は、位相が90度進みます。
ここでは、コンデンサに貯まるエネルギーと電流が進むことを説明します。
コンデンサに貯まるエネルギーの公式
静電容量 \(C\) [F] のコンデンサに電圧を加えると、コンデンサにはエネルギーが蓄えられます。
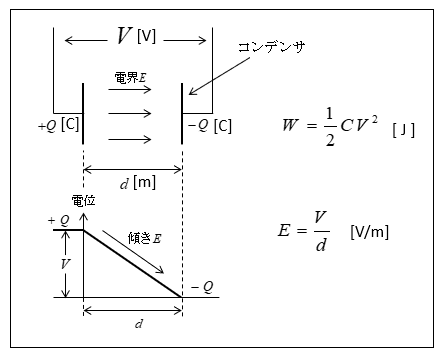
図のように、静電容量 \(C\) [F] のコンデンサに
\(V\) [V] の電圧を加えたときに
コンデンサに蓄えられるエネルギー \(W\) は、次のようになります。
\(W=\cfrac{1}{2}CV^2\) [J]
コンデンサに蓄えられるエネルギー \(W\) [J] は
\(W=\cfrac{1}{2}QV\) [J]
\(Q=CV\) の公式を代入して書き換えると
\(W=\cfrac{1}{2}CV^2=\cfrac{Q^2}{2C}\) [J] になります。
また、電界の強さは、次のようになります。
\(E=\cfrac{V}{d}\) [V/m]
コンデンサに流れる電流が90°進むわけ
コンデンサに流れる電流が90°進むわけ

交流回路にコンデンサを接続した回路の電圧と電流の式は次のようになります。
\(v=E_m\sinωt\quad\rm[V]\)
\(i=ωCE_m\sin\left(ωt+\cfrac{π}{2}\right)\quad\rm[A]\)
\(I_m=ωCE_m\)
電圧を基準に見た場合
交流電源にコンデンサを接続した回路の場合、
電圧の波形に対して、電流の波形が \(\cfrac{π}{2}\)(90°) 進みます。
電圧 \(v\) を基準に考えると \(v\) と \(i\) は次のようになります。
\(v=E_m\sinωt\) [V]
\(i=ωCE_m\sin\left(ωt+\cfrac{π}{2}\right)\) [A]
\(I_m=ωCE_m\)
式を見れば分かる通り、\(i\) は \(v\) より \(\cfrac{π}{2}\) [rad] 進んでいることが分かります。
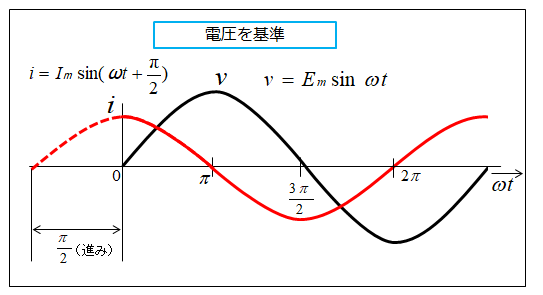
電流が電圧より90°進むことの説明
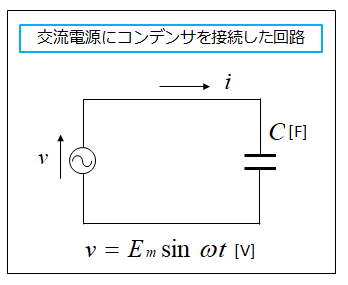
図の回路のコンデンサ C に、正弦波交流電圧 \(v\) を加えると電流 \(i\) が流れます。
電流の定義 \(I=\cfrac{Q}{t}\) [A] から
\(Δt\) 秒間に \(ΔQ\) [C] の電荷が移動した場合の電流 \(i\) は、次のようになります。
\(i=\cfrac{ΔQ}{Δt} \cdots(1)\)
また、コンデンサの静電容量 \(C\) [F]、電荷 \(Q\) [C]、電圧 \(V\) [V] との間には \(Q=CV\) の関係がありますから
\(ΔQ=CΔv \cdots(2)\)
式(2)を式(1)に代入すると
\(i=C\left(\cfrac{Δv}{Δt}\right) \cdots(3)\)
★ 時刻が \(t\) 秒から \(Δt\) 秒経過後の電圧 \(v\)
コンデンサに加わる正弦波交流電圧の \(t\) 秒の瞬時値を \(v_1\) とすると
\(v_1=E_m\sinωt \cdots(4)\)
\(Δt\) 秒後の瞬時値を \(v_2\) とすると
\(v_2=E_m\sin(ωt+ωΔt) \cdots(5)\)
電圧の変化 \(Δv\) とすると
\(Δv=v_2-v_1\)\(=v_2\)
\(=E_m\sin(ωt+ωΔt)-E_m\sinωt \cdots(6)\)
式(6)の \(\sin(ωt+ωΔt)\) は加法定理から
\(\sin(ωt+ωΔt)\)\(=\sinωt\cdot\cosωΔt+\cosωt\)\(\cdot\sinωΔt \cdots(7)\)
また、\(Δt\) を非常に小さい時間とすると
\(\cosωΔt≒\cos0=1、\sinωΔt≒ωΔt\) になりますから、式(7)は
\(\sin(ωt+ωΔt)\)\(=\sinωt\cdot1+\cosωt\cdotωΔt \cdots(8)\)
式(6)の電圧の変化 \(Δv\) は
\(Δv=E_m(\sin(ωt+\cosωt\cdotωΔt)-E_m\sinωt\)
\(Δv=E_m\sinωt+E_m\cosωt\cdotωΔt-E_m\sinωt\)
\(Δv=E_m\cosωt\cdotωΔt\cdots(9)\)
式(9)を式(3)に代入すると
\(i=C\cfrac{Δv}{Δt}\)\(=C\cfrac{E_mωΔt \cdot\cosωt}{Δt}\)
\(i=ωCE_m\cosωt \cdots(10)\)
また、\(\cosωt=\sin(ωt+\cfrac{π}{2})\) ですから
\(i=ωCE_m\cosωt\)=\(ωCE_m\sin(ωt+\cfrac{π}{2}) \cdots(11)\)
となりますので、電流 \(i\) は電圧 \(v\) より \(\cfrac{π}{2}\) [rad] 進んでいることがわかります。
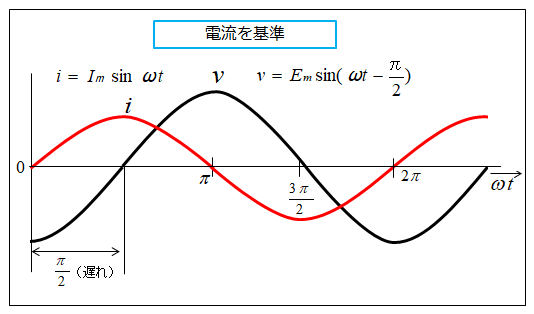
電流を基準に見た場合
交流電源にコンデンサを接続した回路の場合、
電流の波形に対して、電圧の波形が \(\cfrac{π}{2}\)(90°) れます。
\(i=I_m\sinωt\) [V]
\(v=\cfrac{I_m}{ωC}\sin\left(ωt-\cfrac{π}{2}\right)\) [A]
\(E_m=\cfrac{I_m}{ωC}\)
式を見れば分かる通り、\(v\) は \(i\) より \(\cfrac{π}{2}\) [rad] 遅れていることが分かります。
コンデンサに蓄えられるエネルギーの公式のまとめ
\(Q=CV\) [C]
\(W=\cfrac{1}{2}QV\) [J]
\(W=\cfrac{1}{2}CV^2=\cfrac{Q^2}{2C}\) [J]
\(E=\cfrac{V}{d}\) [V/m]
以上で「コンデンサに貯まるエネルギーと電流の位相が進むわけ」の説明を終わります。