電位とは、基準とする地点からの高さを意味します。
また、その地点における位置エネルギーということもできます。
プラスの電荷は、山の形 をしていると考えると頂上の方が、電位が高いということになります。
マイナスの電荷は、谷の形 をしているので底の方が、電位が低いと考えることができます。
電位(点電荷)
図のように、点電荷 \(Q\) から \(r\) [m] 離れた
+1 [C] の電荷の電位は、次のようになります。
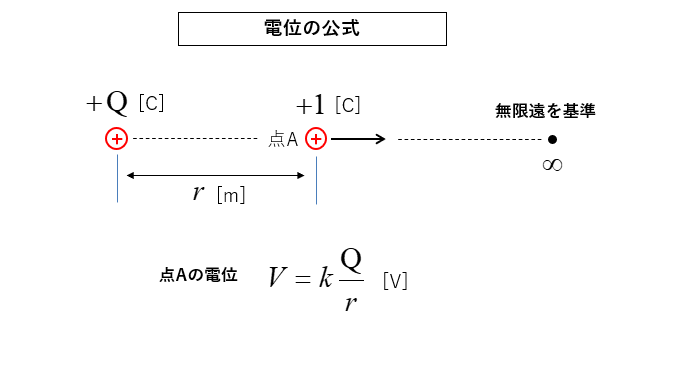
電位の公式
\(V=k\cfrac{Q}{r}\) [V]
電位の定義
電位 \(V \cdots\) +1 [C] の電荷が持つ静電気力の位置エネルギー(スカラー量)
電荷が持つ位置エネルギー
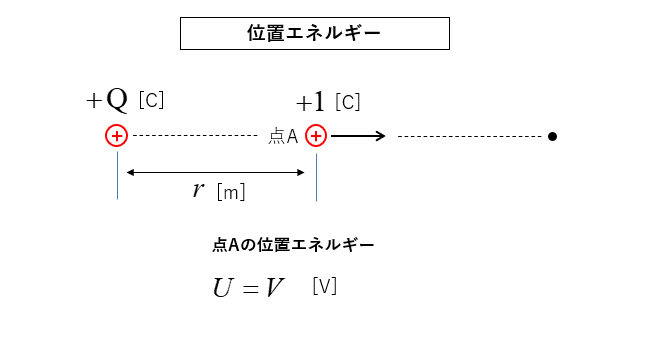
図の点Aの電位が
\(V=k\cfrac{Q}{r}\) [V] の場合
位置エネルギー \(U\) は
\(U=V\) [V]=[J/C] になります。
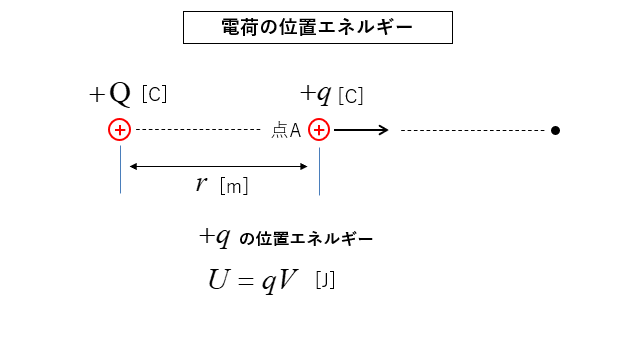
電荷の位置エネルギー
★ 点Aに \(+q\) [C] の電荷を置いた場合の
電荷の持つ位置エネルギーは
\(U=qV\) [J] になります。
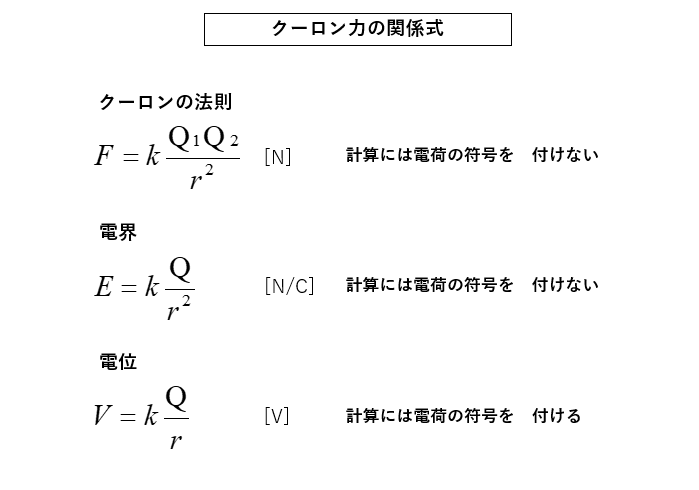
クーロンの法則、点電荷の電界、点電荷の電位の関係
★ クーロンの法則と電界は電荷の符号がわかれば方向が決まるので
計算は大きさだけを考えれば良いので符号は付けないで計算します。
★ 電位の場合は電荷から見て、プラスのときもマイナスのときも考えられるので符号を付けて計算します。
電位(一様な電界)
点A の電位 \(V\) は
+1 [C] の電荷を点A から基準点O まで移動した仕事になります。
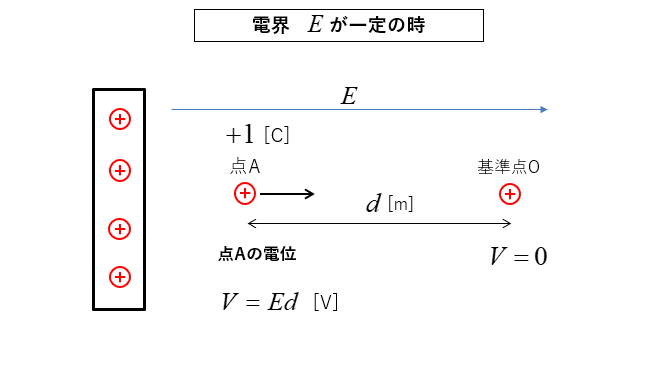
仕事=力 × 距離 なので
\(V=Ed\) [V] になります。
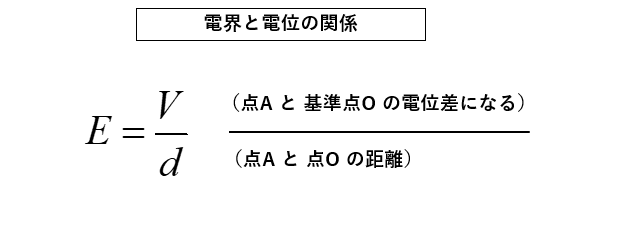
電場と電位の関係
電位の式を変形すると、次のようになります。
\(E=\cfrac{V}{d}\) [V/m]
電位の公式
\(V=k\cfrac{Q}{r}\) [V]
電荷が持つ位置エネルギー
\(U=qV\) [J]
\(U=k\cfrac{Qq}{r}\)
一様な電界中の電位
\(V=Ed\) [V]
練習問題
問題1
図の二つの電位 \(V\) の合計を求めよ。
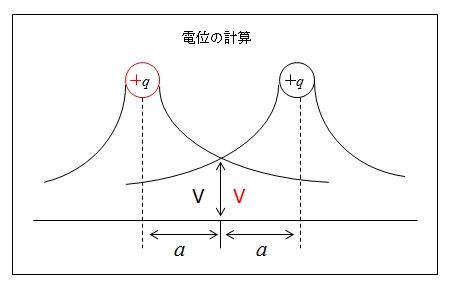
<解答例>
2つの電荷 \(q\) による電位は共に同じになります。
\(V=k\cfrac{q}{a}\) [V]
電位 \(V\) の足し算は数値で計算する。(向きは関係なし)
\(2V=k\cfrac{q}{a}+k\cfrac{q}{a}=\cfrac{2kq}{a}\) [V] になります。
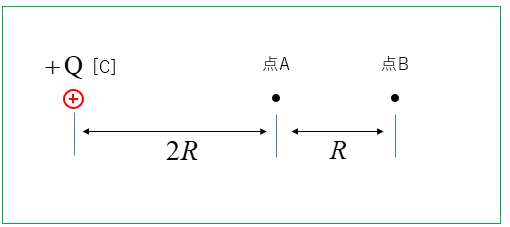
問題2
図のように、点電荷 \(+Q\) から \(2R\) 離れた所を 点A
点Aから \(R\) 離れた所を 点B とします。
クーロンの法則の比例定数を \(k\)、電位は無限遠を基準として次の問いに答えよ。
- 点Aにおける電場の大きさを求めよ。
- 点A、点B における電位を求めよ。
<解答例1>
■ 点Aにおける電場の大きさは公式から
\(E=k\cfrac{Q}{r^2}=k\cfrac{Q}{(2R)^2}\)
\(E=k\cfrac{Q}{4R^2}\) [N/C] になります。
<解答例2>
■ 点A の電位は電位の式から
\(V=k\cfrac{Q}{r}\)
\(V_A=k\cfrac{Q}{2R}\) [V]
点B の電位は
\(V_B=k\cfrac{Q}{3R}\) [V]
以上で「電位とは」の説明を終わります。