- 三相交流の結線方式の種類
- スター結線(Y結線・星型結線)の特徴
- デルタ結線(Δ結線)の特徴
について説明しています。
三相結線の種類
代表的な三相交流の結線方法として 「スター結線」 と 「デルタ結線」 があります。
スター結線は「Y結線」または「星型結線」といいます。
また、デルタ結線は「Δ結線」または「三角結線」といいます。
三相電源と三相負荷の結線種類
三相交流回路の電源側と負荷側を接続する方法には 次の4種類があります。
- Y-Y結線
電源側と負荷側がともにスター結線 - Y-Δ結線
電源側がスター結線で負荷側がデルタ結線 - Δ-Δ結線
電源側と負荷側がともにデルタ結線 - Δ-Y結線
電源側がデルタ結線で負荷側がスター結線
電源側がスター結線
■ 電源側がスター結線で、負荷側がスター結線または、デルタ結線のとき
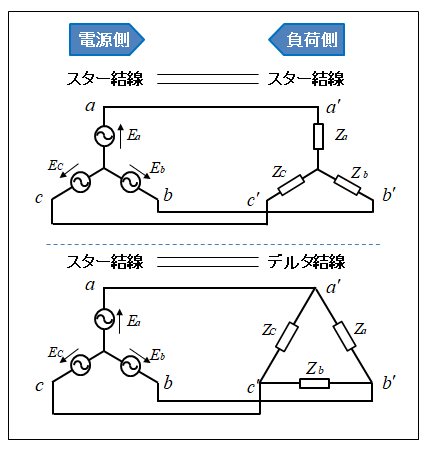
スター結線の線間電圧は 相電圧の ルート3倍 になります。
電源側がデルタ結線
■ 電源側がデルタ結線で、負荷側がデルタ結線または、スター結線のとき
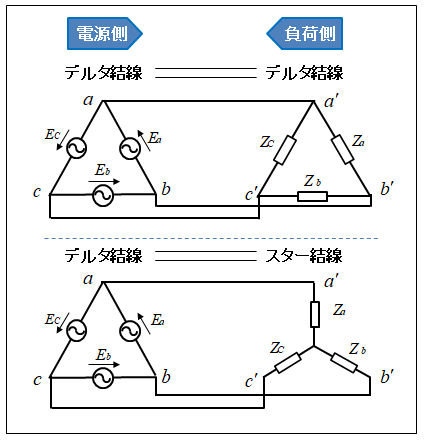
デルタ結線の線電流 は 相電流の ルート3倍 になります。
スター結線については三相交流のスター結線を参考にしてください。
デルタ結線については三相交流のデルタ結線」を参考にしてください。
スター結線(Y結線・星型結線)の特徴
■ スター結線の特徴
- 線間電圧は相電圧の \(\sqrt3\) 倍 になります。
- 線間電圧の位相は相電圧より \(\cfrac{π}{6}\) (30度) 進みます。
- スター結線の線電流と相電流は等しい。
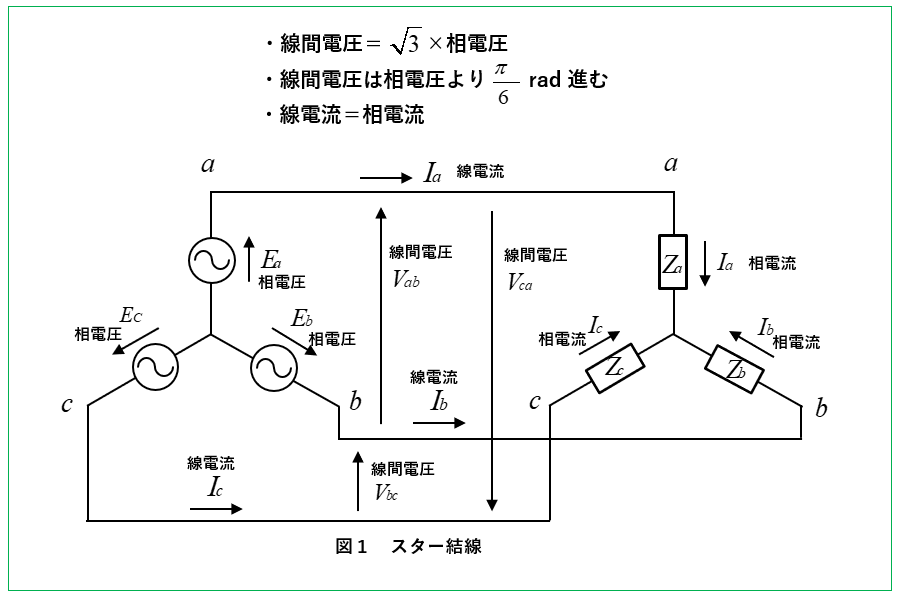
線間電圧の求め方
\(V_{ab}\)\(=E_a-E_b\)\(=E_a+(-E_b)\) [V]
\(V_{bc}\)\(=E_b-E_c\)\(=E_b+(-E_c)\) [V]
\(V_{ca}\)\(=E_c-E_a\)\(=E_c+(-E_a)\) [V]
ベクトル図から線間電圧を求める
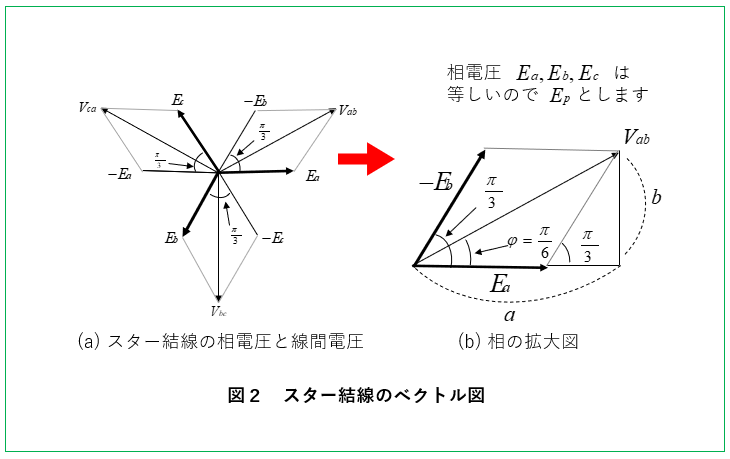
図2の(b)から線間電圧 \(V_{ab}\) を求める。
\(V_{ab}=E_a-E_b=E_a+(-E_b)\) でベクトル和になります。
各相電圧は等しいので \(E_P\) とすると
\(V_{ab}\)\(=\sqrt{a^2+b^2}\)\(=\sqrt{\left(E_P+E_P\cos\cfrac{π}{3}\right)^2+\left(E_P\sin\cfrac{π}{3}\right)^2}\)
\(V_{ab}=\sqrt{\left(E_P+\cfrac{1}{2}E_P\right)^2+\left(\cfrac{\sqrt3}{2}E_P\right)^2}\)
\(=\sqrt{\left(\cfrac{3}{2}E_P\right)^2+\left(\cfrac{\sqrt3}{2}E_P\right)^2}\)
\(=\sqrt{\cfrac{12}{4}{E_P}^2}=\sqrt{3{E_P}^2}\)
\(=\sqrt3E_P\)
デルタ結線(Δ結線・三角結線)の特徴
■ デルタ結線の特徴
- 線電流は相電流の (\sqrt3) 倍 になります。
- 線電流の位相は相電流より (\cfrac{π}{6}) (30度) 遅れます。
- デルタ結線の線間電圧と相電圧は等しい。
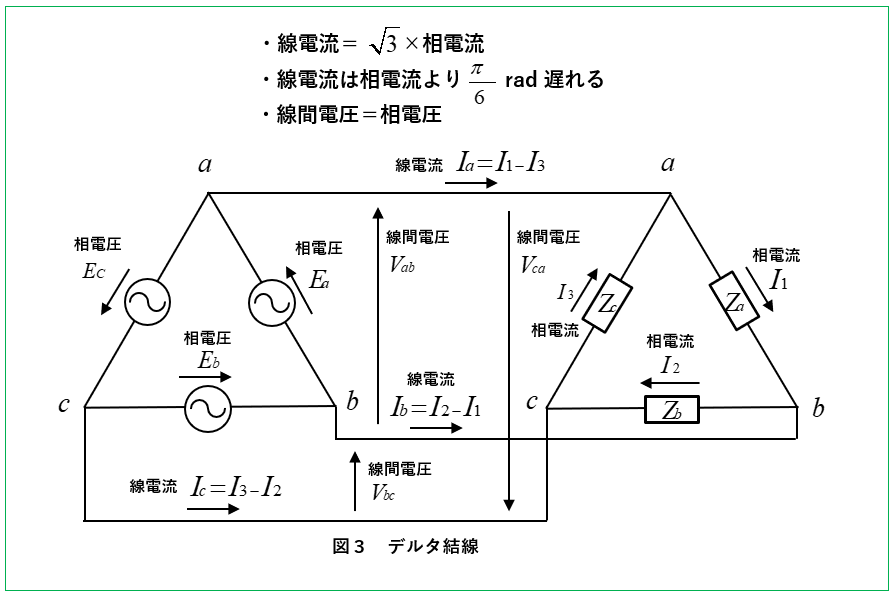
線電流の求め方
\(I_a=I_1-I_3=I_1+(-I_3)\) [A]
\(I_b=I_2-I_1=I_2+(-I_1)\) [A]
\(I_c=I_3-I_2=I_3+(-I_2)\) [A]
ベクトル図から線電流を求める
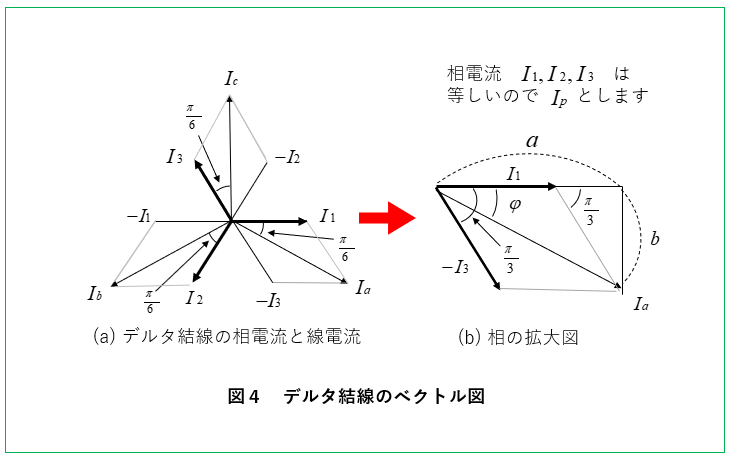
図4の(b)から線電流 \(I_a\) を求めます。
\(I_a=I_1-I_3=I_1+(-I_3)\) でベクトル和になります。
各相電流は等しいのでので \(I_P\) とすると
\(I_a=\sqrt{a^2+b^2}\)
\(=\sqrt{\left(I_P+I_P\cos\cfrac{π}{3}\right)^2+\left(I_P\sin\cfrac{π}{3}\right)^2}\)
\(I_a=\sqrt{\left(I_P+\cfrac{1}{2}I_P\right)^2+\left(\cfrac{\sqrt3}{2}I_P\right)^2}\)
\(=\sqrt{\left(\cfrac{3}{2}I_P\right)^2+\left(\cfrac{\sqrt3}{2}I_P\right)^2}\)
\(=\sqrt{\cfrac{12}{4}{I_P}^2})(=\sqrt{3{I_P}^2}\)
\(=\sqrt3I_P\)
三相結線の種類まとめ
スター結線とデルタ結線の特徴は次のようになります。

V結線とは
三相交流のスター結線
三相交流のデルタ結線
平衡三相負荷のデルタ・スター変換公式とスター・デルタ変換公式
不平衡三相負荷の変換公式と公式の求め方