平衡三相負荷のデルタ・スター変換公式とスター・デルタ変換公式

三相負荷の結線方式を、デルタ結線からスター結線に変換または、スター結線からデルタ結線に変換することができます。

三相負荷のインピーダンスが等しい負荷のことを、三相平衡負荷といいます。この記事では、三相平衡負荷の変換公式を説明します。

平衡三相負荷のデルタ・スター（Δ－Y）変換公式

三相平衡負荷回路において、デルタ・スター変換公式は次のようになります。

デルタ負荷のインピーダンスを　\(Z_Δ\)　、スター負荷のインピーダンスを　\(Z_Y\)　とすると

\(Z_Y=\cfrac{1}{3}Z_Δ\)

スター負荷は　デルタ負荷の　\(\cfrac{1}{3}\)　倍になります。

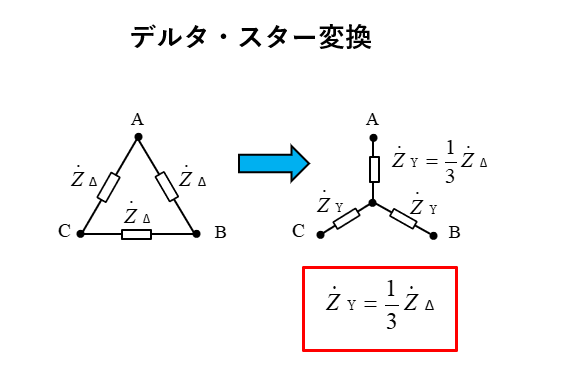
デルタ・スター変換公式の求め方

デルタ・スター変換公式を求めるには、デルタ結線の負荷とスター結線の負荷が等しいと仮定します。

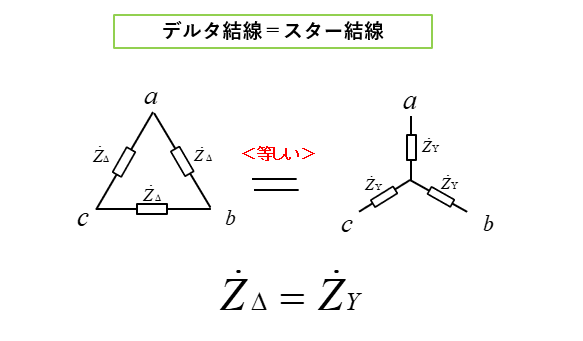
端子ab間のインピーダンス を求める

三相平衡負荷なので、1つの相について求めれば良いことになります。

デルタ負荷の端子ab間の合成インピーダンスを　\(Z_{Δab}\)　、各相のインピーダンスを　\(Z_Δ\)　とし

スター負荷の端子ab間のインピーダンスを　\(Z_{Yab}\)　、各相のインピーダンスを　\(Z_Y\)　とします。

デルタ負荷とスター負荷が等しいので
\(Z_{Δab}=Z_{Yab}\)　です。

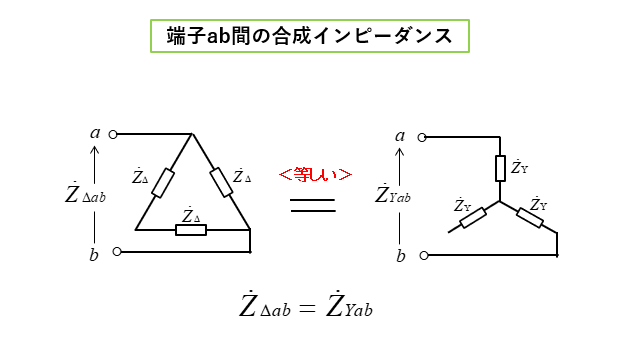
■　デルタ負荷の端子ab間のインピーダンス

デルタ負荷の端子ab間のインピーダンスは、図のように直並列の合成インピーダンスです。
各相のインピーダンスを　\(Z_Δ\)　とすると

\(Z_{Δab}=\cfrac{2}{3}Z_Δ\cdots(1)\)

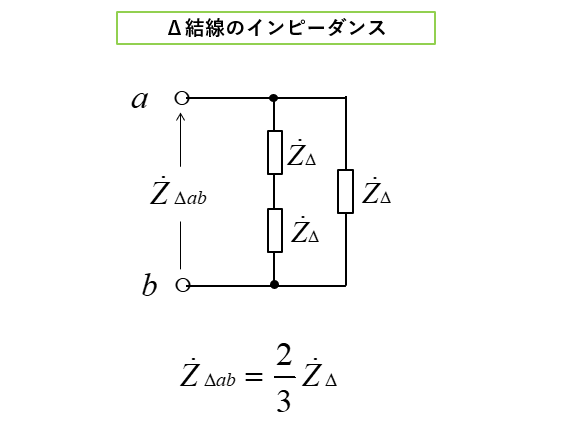
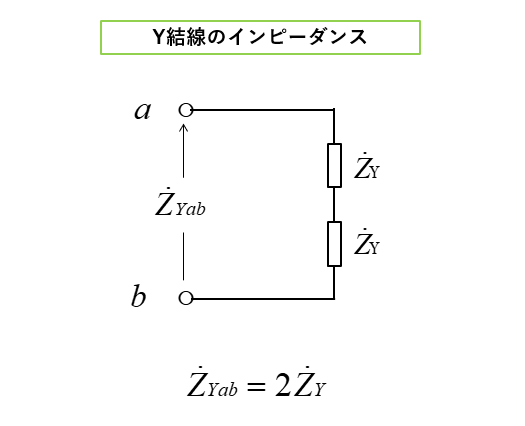
■　スター負荷の端子ab間のインピーダンス

スター負荷の端子ab間のインピーダンスは、図のように直列の合成インピーダンスです。

\(Z_{Yab}=2Z_Y\cdots(2)\)

式（1）と式（2）が等しいので
\(Z_{Δab}=Z_{Yab}\) ですから

\(\cfrac{2}{3}Z_Δ=2Z_Y\)

\(Z_Y=\cfrac{1}{3}Z_Δ\)　になります。

平衡三相負荷のスター・デルタ（Y－Δ）変換公式

三相平衡負荷回路において、スター・デルタ変換公式は次のようになります。

スター負荷のインピーダンスを　\(Z_Y\)　、デルタ負荷のインピーダンスを　\(Z_Δ\)　とすると

\(Z_Δ=3Z_Y\)

デルタ負荷は　スター負荷の　3倍になります。

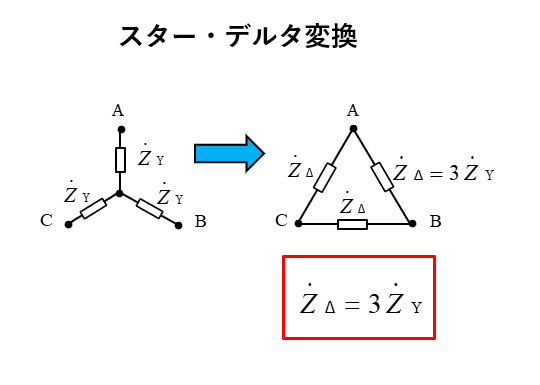
スター・デルタ変換公式の求め方

スター・デルタ変換公式を求めるには、スター結線の負荷とデルタ結線の負荷が等しいと仮定します。

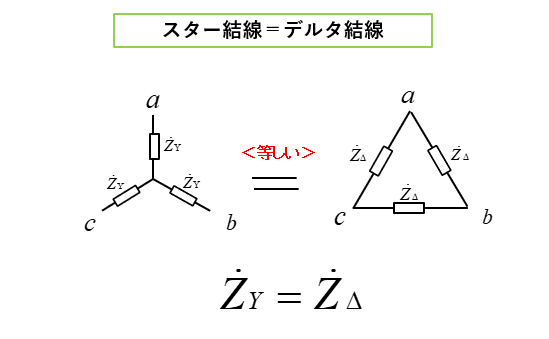
端子 ab間のインピーダンス

三相平衡負荷なので、1つの相について求めれば良いことになります。

スター負荷の端子ab間のインピーダンスを　\(Z_{Yab}\)　、各相のインピーダンスを　\(Z_Y\)　とし

デルタ負荷の端子ab間のインピーダンスを　\(Z_{Δab}\)　、各相のインピーダンスを　\(Z_Δ\)　とします。

スター負荷とデルタ負荷が等しいので
\(Z_{Yab}=Z_{Δab}\)　です。

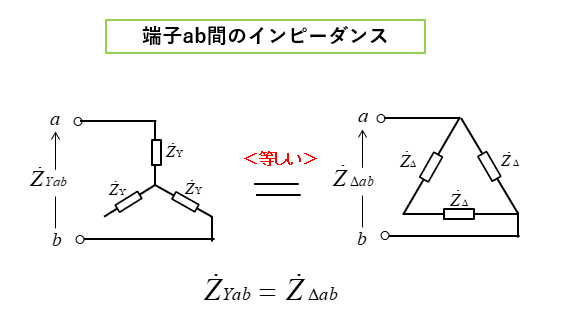
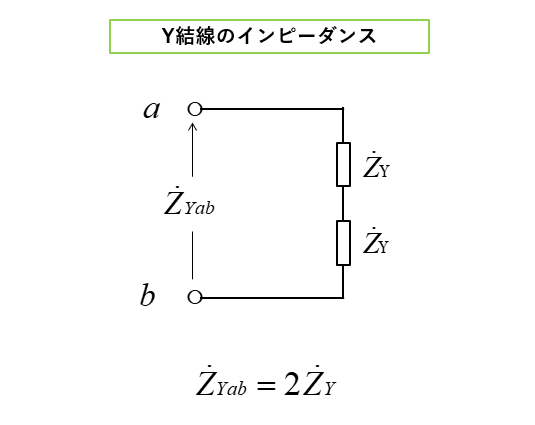
■　スター負荷の端子ab間のインピーダンス

スター負荷の端子ab間のインピーダンスは、図のように直列の合成インピーダンスです。
各相のインピーダンスを　\(Z_Y\)　とすると

\(Z_{Yab}=2Z_Y\cdots(3)\)

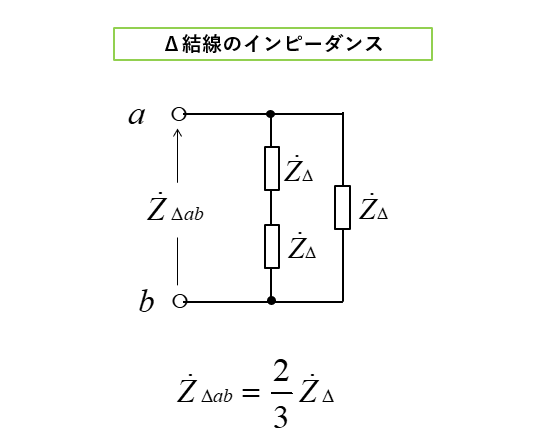
■　デルタ負荷の端子ab間のインピーダンス

デルタ負荷の端子ab間のインピーダンスは、図のように直並列の合成インピーダンスです。

\(Z_{Δab}=\cfrac{2}{3}Z_Δ\cdots(4)\)

式（3）と式（4）が等しいので
\(Z_{Yab}=Z_{Δab}\) ですから

\(2Z_Y=\cfrac{2}{3}Z_Δ\)

\(Z_Δ\)\(=3Z_Y\)　になります。

まとめ

不平衡三相負荷の変換公式と公式の求め方
三相結線の種類