三相負荷が不平衡になると、変換公式が難しくなります。
- 不平衡のデルタスター変換公式
- 不平衡のスターデルタ変換公式
この記事では、不平衡三相負荷の変換公式と公式の求め方 を説明します。
不平衡三相負荷のデルタスター(Δ-Y)変換公式
不平衡三相負荷の場合は
各インピーダンスの大きさが異なります。
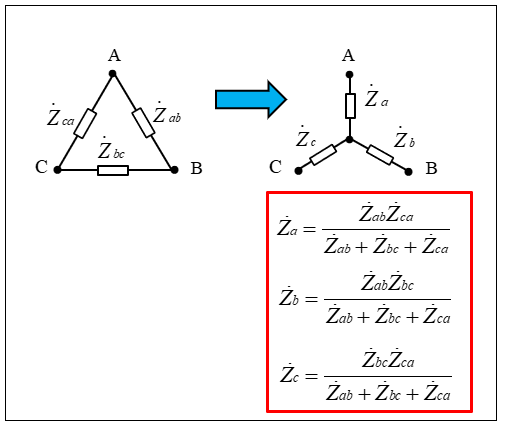
デルタスター(ΔーY)変換公式
デルタ結線負荷を スター結線負荷に変換すると、次の式になります。
\(Z_{a}=\)\(\cfrac{Z_{ab}Z_{ca}}{Z_{ab}+Z_{bc}+Z_{ca}}\)
\(Z_{b}=\)\(\cfrac{Z_{ab}Z_{bc}}{Z_{ab}+Z_{bc}+Z_{ca}}\)
\(Z_{c}=\)\(\cfrac{Z_{bc}Z_{ca}}{Z_{ab}+Z_{bc}+Z_{ca}}\)
デルタスター(ΔーY)変換公式の覚え方
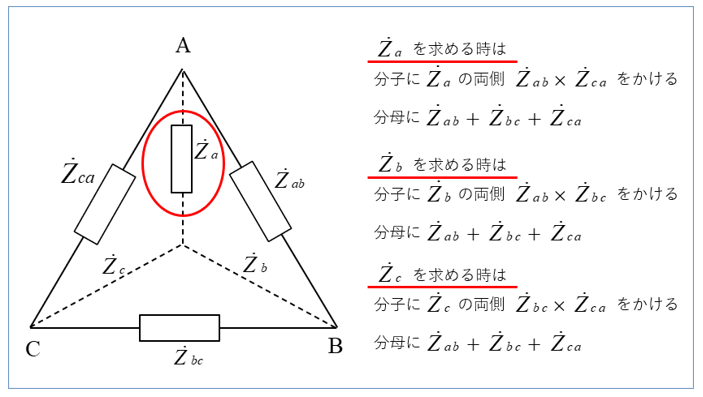
\(Z_{a}=\)\(\cfrac{Z_{ab}Z_{ca}}{Z_{ab}+Z_{bc}+Z_{ca}}\)
\(Z_{b}=\)\(\cfrac{Z_{ab}Z_{bc}}{Z_{ab}+Z_{bc}+Z_{ca}}\)
\(Z_{c}=\)\(\cfrac{Z_{bc}Z_{ca}}{Z_{ab}+Z_{bc}+Z_{ca}}\)
不平衡三相負荷のスターデルタ(Y-Δ)変換公式
不平衡三相負荷の場合は
各インピーダンスの大きさが異なります。
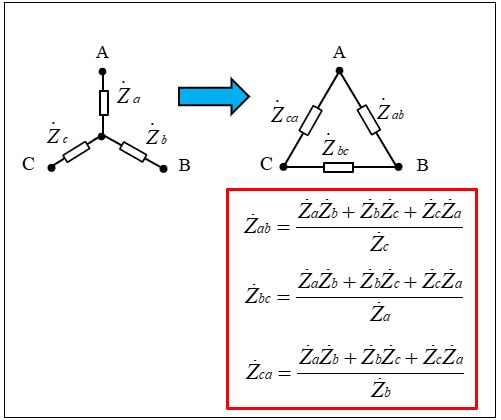
スターデルタ(YーΔ)変換公式
スター結線負荷を デルタ結線に変換すると、次の式になります。
\(Z_{ab}=\)\(\cfrac{Z_{a}Z_{b}+Z_{b}Z_{c}+Z_{c}Z_{a}}{Z_{c}}\)
\(Z_{ab}=\)\(\cfrac{Z_{a}Z_{b}+Z_{b}Z_{c}+Z_{c}Z_{a}}{Z_{a}}\)
\(Z_{ab}=\)\(\cfrac{Z_{a}Z_{b}+Z_{b}Z_{c}+Z_{c}Z_{a}}{Z_{b}}\)
スターデルタ(YーΔ)変換公式の覚え方

\(Z_{ab}=\)\(\cfrac{Z_{a}Z_{b}+Z_{b}Z_{c}+Z_{c}Z_{a}}{Z_{c}}\)
\(Z_{ab}=\)\(\cfrac{Z_{a}Z_{b}+Z_{b}Z_{c}+Z_{c}Z_{a}}{Z_{a}}\)
\(Z_{ab}=\)\(\cfrac{Z_{a}Z_{b}+Z_{b}Z_{c}+Z_{c}Z_{a}}{Z_{b}}\)
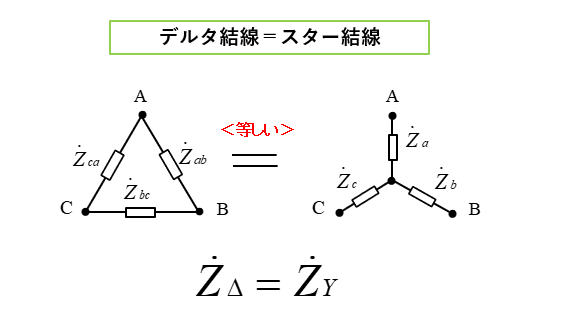
デルタスター変換公式の求め方
変換公式を求めるには
デルタ結線の負荷とスター結線の負荷の
合成インピーダンスが等しいと仮定します。
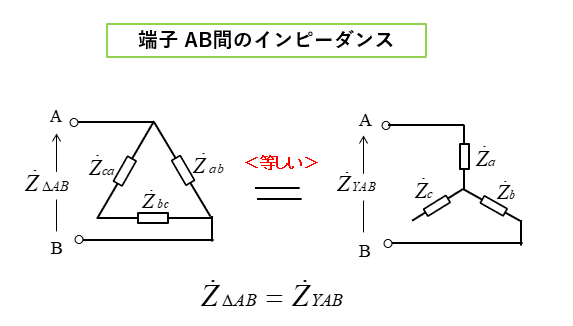
端子 AB間のインピーダンス
■ Δ結線の端子 AB間のインピーダンス
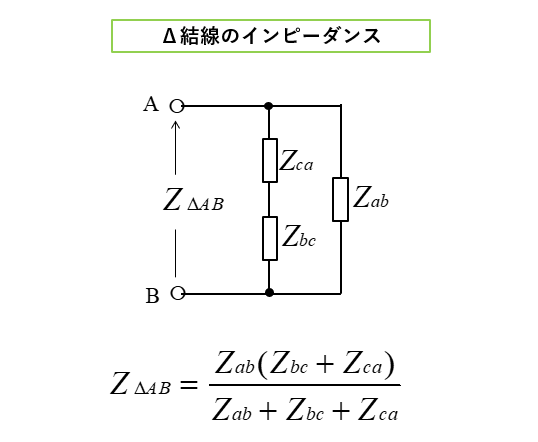
\(Z_{ΔAB}=\cfrac{Z_{ab}Z_{ca}+Z_{ab}Z_{bc}}{Z_{ab}+Z_{bc}+Z_{ca}}\)
■ Y結線の端子 AB間のインピーダンス
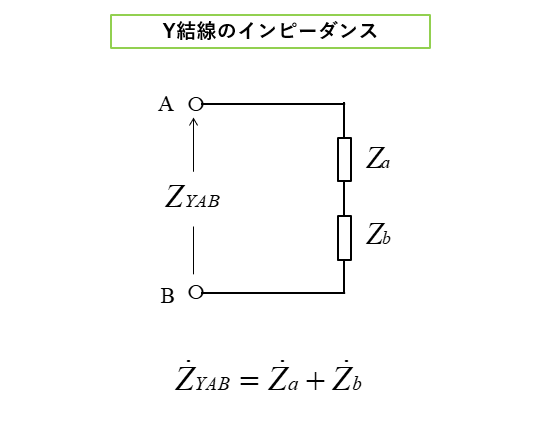
\(Z_{YAB}=Z_{a}+Z_{b}\)
\(Z_{YAB}=Z_{ΔAB}\) より
\(Z_{a}+Z_{b}=\cfrac{Z_{ab}Z_{ca}+Z_{ab}Z_{bc}}{Z_{ab}+Z_{bc}+Z_{ca}}\cdots(1)\)
端子 BC間のインピーダンス
同様にして端子 BC間のインピーダンスを求めます。
■ Δ結線の端子 BC間のインピーダンス
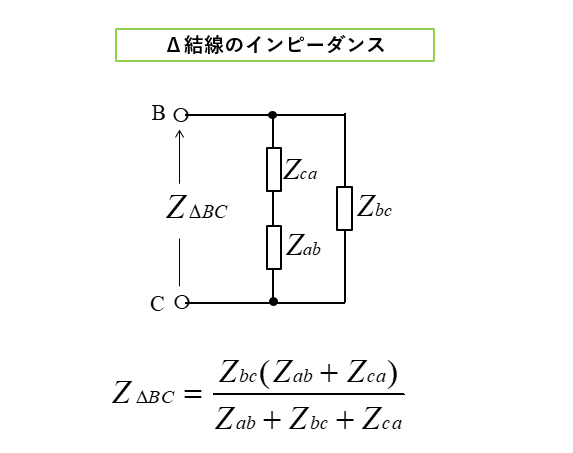
\(Z_{ΔBC}=\cfrac{Z_{ab}Z_{bc}+Z_{bc}Z_{ca}}{Z_{ab}+Z_{bc}+Z_{ca}}\)
■ Y結線の端子 BC間のインピーダンス
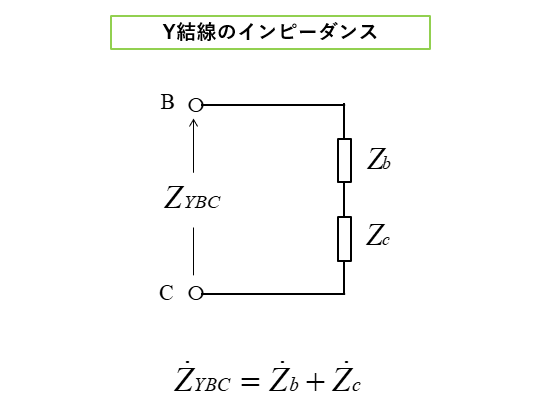
\(Z_{YBC}=Z_{b}+Z_{c}\)
\(Z_{YBC}=Z_{ΔBC}\) より
\(Z_{b}+Z_{c}=\cfrac{Z_{ab}Z_{bc}+Z_{bc}Z_{ca}}{Z_{ab}+Z_{bc}+Z_{ca}}\cdots(2)\)
端子 CA間のインピーダンス
同様にして端子 CA間のインピーダンスを求めます。
■ Δ結線の端子 CA間のインピーダンス
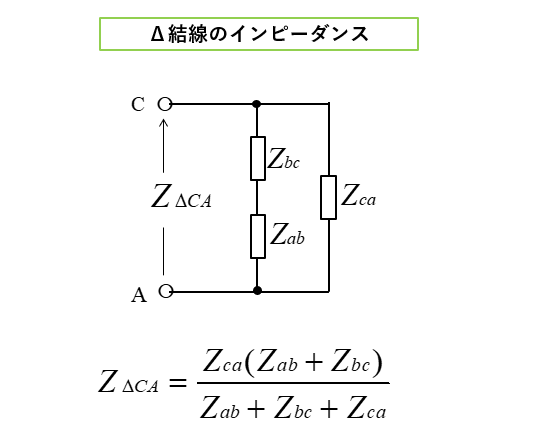
\(Z_{ΔCA}=\cfrac{Z_{ab}Z_{ca}+Z_{ca}Z_{bc}}{Z_{ab}+Z_{bc}+Z_{ca}}\)
■ Y結線の端子 CA間のインピーダンス
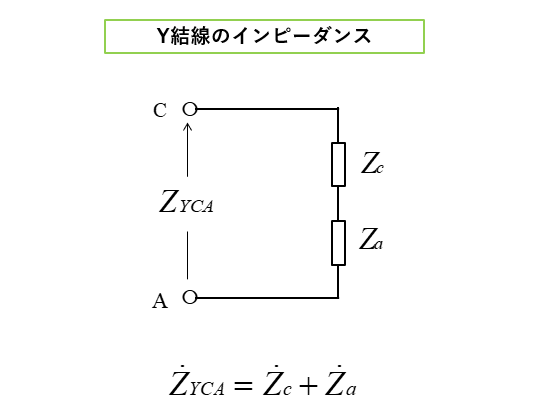
\(Z_{YCA}=Z_{c}+Z_{a}\)
\(Z_{YCA}=Z_{ΔCA}\) より
\(Z_{c}+Z_{a}=\cfrac{Z_{ab}Z_{ca}+Z_{ca}Z_{bc}}{Z_{ab}+Z_{bc}+Z_{ca}}\cdots(3)\)
\(Z_{a}+Z_{b}=\cfrac{Z_{ab}Z_{ca}+Z_{ab}Z_{bc}}{Z_{ab}+Z_{bc}+Z_{ca}}\cdots(1)\)
\(Z_{b}+Z_{c}=\cfrac{Z_{ab}Z_{bc}+Z_{bc}Z_{ca}}{Z_{ab}+Z_{bc}+Z_{ca}}\cdots(2)\)
\(Z_{c}+Z_{a}=\cfrac{Z_{ab}Z_{ca}+Z_{ca}Z_{bc}}{Z_{ab}+Z_{bc}+Z_{ca}}\cdots(3)\)
式(1)から式(2)を引きます。
\(Z_{a}-Z_{c}=\cfrac{Z_{ab}Z_{ca}-Z_{ca}Z_{bc}}{Z_{ab}+Z_{bc}+Z_{ca}}\cdots(4)\)
式(3)と式(4)を足します。
\(2Z_{a}=\cfrac{2Z_{ab}Z_{ca}}{Z_{ab}+Z_{bc}+Z_{ca}}\)
\(Z_{a}=\cfrac{Z_{ab}Z_{ca}}{Z_{ab}+Z_{bc}+Z_{ca}}\cdots(5)\)
式(1)と式(5)から
\(Z_{b}=\cfrac{Z_{ab}Z_{bc}}{Z_{ab}+Z_{bc}+Z_{ca}}\cdots(6)\)
式(2)と式(6)から
\(Z_{c}=\cfrac{Z_{bc}Z_{ca}}{Z_{ab}+Z_{bc}+Z_{ca}}\cdots(7)\)
\(Z_{a}=\cfrac{Z_{ab}Z_{ca}}{Z_{ab}+Z_{bc}+Z_{ca}}\)
\(Z_{b}=\cfrac{Z_{ab}Z_{bc}}{Z_{ab}+Z_{bc}+Z_{ca}}\)
\(Z_{c}=\cfrac{Z_{bc}Z_{ca}}{Z_{ab}+Z_{bc}+Z_{ca}}\)
スターデルタの変換公式の求め方
\(Z_{a}=\cfrac{Z_{ab}Z_{ca}}{Z_{ab}+Z_{bc}+Z_{ca}}\cdots(5)\)
\(Z_{b}=\cfrac{Z_{ab}Z_{bc}}{Z_{ab}+Z_{bc}+Z_{ca}}\cdots(6)\)
\(Z_{c}=\cfrac{Z_{bc}Z_{ca}}{Z_{ab}+Z_{bc}+Z_{ca}}\cdots(7)\)
式(5)、(6)、(7)から \(Z_{a}Z_{b}\)、\(Z_{b}Z_{c}\)、\(Z_{c}Z_{a}\) を求めます。
\(Z_aZ_b=\cfrac{(Z_{ab})^2Z_{ca}Z_{bc}}{(Z_{ab}+Z_{bc}+Z_{ca})^2}\cdots(8)\)
\(Z_bZ_c=\cfrac{(Z_{bc})^2Z_{ab}Z_{ca}}{(Z_{ab}+Z_{bc}+Z_{ca})^2}\cdots(9)\)
\(Z_cZ_a=\cfrac{(Z_{ca})^2Z_{ab}Z_{bc}}{(Z_{ab}+Z_{bc}+Z_{ca})^2}\cdots(10)\)
式(8)、(9)、(10)の両辺を加算します。
\(Z_aZ_b+Z_bZ_c+Z_cZ_a=\cfrac{Z_{ab}Z_{bc}Z_{ca}}{Z_{ab}+Z_{bc}+Z_{ca}}\cdots(11)\)
Zab を求める
\(Z_aZ_b+Z_bZ_c+Z_cZ_a=\cfrac{Z_{ab}Z_{bc}Z_{ca}}{Z_{ab}+Z_{bc}+Z_{ca}}\cdots(11)\)
\(Z_c=\cfrac{Z_{bc}Z_{ca}}{Z_{ab}+Z_{bc}+Z_{ca}}\cdots(7)\)
式(11)の両辺を(7)式の両辺で除算します。
\(Z_{ab}=\cfrac{Z_aZ_b+Z_bZ_c+Z_cZ_a}{Z_c}\cdots(12)\)
Zbc を求めます
\(Z_aZ_b+Z_bZ_c+Z_cZ_a=\cfrac{Z_{ab}Z_{bc}Z_{ca}}{Z_{ab}+Z_{bc}+Z_{ca}}\cdots(11)\)
\(Z_a=\cfrac{Z_{ab}Z_{ca}}{Z_{ab}+Z_{bc}+Z_{ca}}\cdots(5)\)
式(11)の両辺を式(5)の両辺で除算します。
\(Z_{bc}=\cfrac{Z_aZ_b+Z_bZ_c+Z_cZ_a}{Z_a}\cdots(13)\)
Zca を求めます
\(Z_aZ_b+Z_bZ_c+Z_cZ_a=\cfrac{Z_{ab}Z_{bc}Z_{ca}}{Z_{ab}+Z_{bc}+Z_{ca}}\cdots(11)\)
\(Z_b=\cfrac{Z_{ab}Z_{bc}}{Z_{ab}+Z_{bc}+Z_{ca}}\cdots(6)\)
式(11)の両辺を式(6)の両辺で除算します。
\(Z_{ca}=\cfrac{Z_aZ_b+Z_bZ_c+Z_cZ_a}{Z_b}\cdots(14)\)
以上のように、変換公式を求めることができます。
まとめ
不平衡三相負荷の変換公式は次のとおりです。
デルタスター変換公式

スターデルタ変換公式
