ヒステリシス曲線は、全く磁化されていない磁性体に磁界を加えた時の、磁界と磁束密度の関係を曲線として描いたものです。
磁性体と磁化曲線、残留磁化、保持力について説明します。
ヒステリシス曲線とは
ヒステリシス曲線は
全く磁化されていない磁性体に磁界を加えた時の
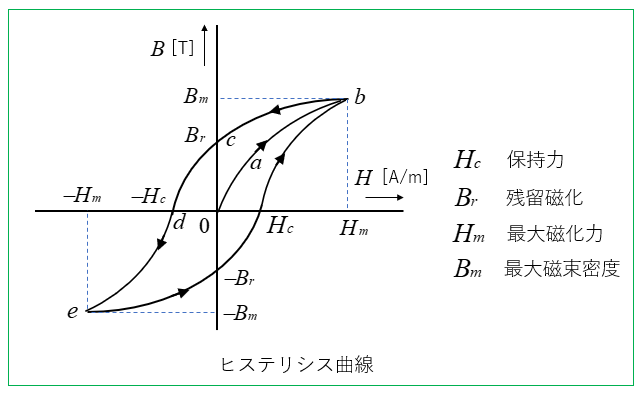
ヒステリシス曲線
- ゼロから磁界を加えていくと \(a\) のような曲線になり \(b\) まで行きます。
- 次に磁界を弱くしていくと、もとの曲線に戻らず \(c\) の曲線をたどります。
- 磁界 \(H\) をゼロにしても、ある強さの磁化が残ります。
- この磁化 \(B_r\) を 残留磁化 といいます。
- 更に磁界 \(H\) を最初と逆方向に加えると、磁化はゼロになります。
- このときの、磁界の強さ \(H_c\) を 保磁力 といいます。
- このように磁界 \(H\) を
\(-H_m\leq H\leq H_m\) の範囲で変化させると
それに対応した磁化の範囲で変化します。
この曲線をヒステリシス曲線(ヒステリシスループ、履歴曲線) といいます。

ヒステリシス曲線のエネルギー
ヒステリシス曲線を一回りすると、\(B\) と \(H\) はもとの値に戻ります。
このとき、加えられたエネルギーはすべて熱となります。
また、ヒステリシス曲線を一回りするときに
外部から単位体積毎に加えられるエネルギーは、このループによって囲まれる面積に等しい。
このときの単位体積当たりのエネルギーを \(P_{h1}\) とすると
\(P_{h1}=\eta {B_m}^{1.6}f\) [W/m3] となります。
\(B_m \cdots\)最大磁束密度
\(\eta \cdots\)磁性体の定数でヒステリシス係数です。
(\(\eta\) の値は\(10^2~10^3\) 程度)
\(\eta\) の読みはイータまたはエータ)
\(f\) [Hz]\(\cdots\)周波数
磁性体の体積を \(V\) [m3] とすると
\(P_h=\eta {B_m}^{1.6}f\cdot V\) [W] となります。
この電力 \(P_h\) を ヒステリシス損 と呼びます。
磁性体
図のような、磁性体の環状鉄心ソレノイドに電流を流します。
環状鉄心ソレノイドの磁界は、鉄心の内部に発生します。
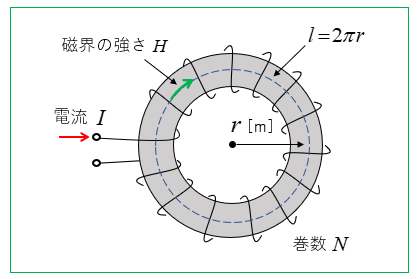
このとき、内部に発生する磁界 \(H\) は
\(H=\cfrac{NI}{2πr}\) [A/m]
磁束密度 \(B\) は
\(B=μH=μ_0μ_rH\) [T]
透磁率は磁気を通す比率を表します。
\(k=\cfrac{1}{4πμ_0}≒6.33×10^4\) [N・m2/Wb2]\(\cdots\)定数
\(μ_0=4π×10^{-7}\) [H/m]\(\cdots\)真空の透磁率
\(μ=μ_0μ_r\) [H/m]\(\cdots\)透磁率で「ミュー」と読みます。
\(μ_r=\cfrac{μ}{μ_0}\cdots\)比透磁率 空気中では、\(μ_r=1\) です。
\(k=\cfrac{1}{4πμ}\cdots\)透磁率 \(μ\) の媒質中の定数
磁化曲線
磁界の強さ \(H\) と磁束密度 \(B\) の関係をグラフにすると、次のようになります。
■ 磁化曲線
- 全く磁化されていない磁性体に、一定方向の磁界 \(H\) を加えて得られた曲線です。
- 磁界 \(H\) を増加させていくと、徐々に磁束密度 \(B\) が大きくなります。
- 磁界 \(H\) を増加させても、磁束密度 \(B\) が増加しなくなる 飽和現象 を示します。

磁束密度と磁界の強さの関係から
\(B=μH=μ_0μ_rH\) [T]
透磁率 \(μ\) は
\(μ=\cfrac{B}{H}=\tanθ\) として求められます。
電気機器と残留磁化と保磁力の大きさの関係
残留磁化と保磁力の大小は、それに適する電気機器があります。
次の図のように、残留磁化と保磁力が大きい材料は 永久磁石 として適しています。
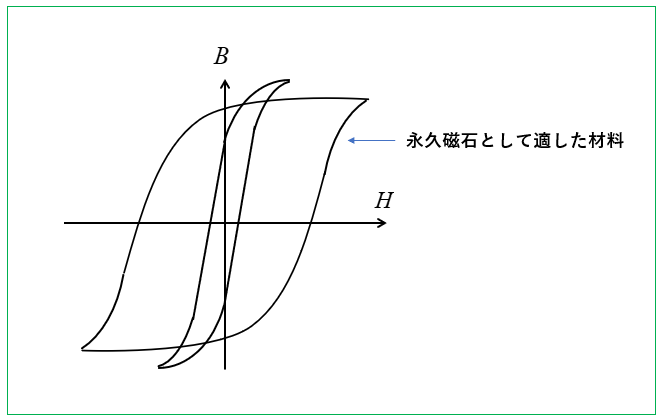
また、変圧器等の鉄心の材料としては、ヒステリシス曲線が急に立ち上がり、その幅が狭く、小さな磁界の変化に対して大きな磁化の変化があるものが望ましいとされます。

以上で「ヒステリシス曲線とは」の説明を終わります。