交流回路における
抵抗だけ・コイルだけ・コンデンサだけの回路の
電圧と電流の位相、インピーダンスについて説明します。
| 素子 | 記号 | 電流 | 電流との位相差 |
|---|---|---|---|
| 抵抗 | \(R\) | \(\dot{E}=R\dot{I}\) | 同相 |
| コイル | \(L\) | \(\dot{E}=jωL\dot{I}\) | 電圧が \(\cfrac{π}{2}\) 進む |
| コンデンサ | \(C\) | \(\dot{E}=\cfrac{\dot{I}}{jωC}\) | 電圧が \(\cfrac{π}{2}\) 遅れる |
コイルとコンデンサの位相の覚え方については、こちらの記事が参考になります。
抵抗だけの交流回路
抵抗だけの交流回路の電圧と電流の瞬時値
抵抗 \(R\) だけの交流回路があります。
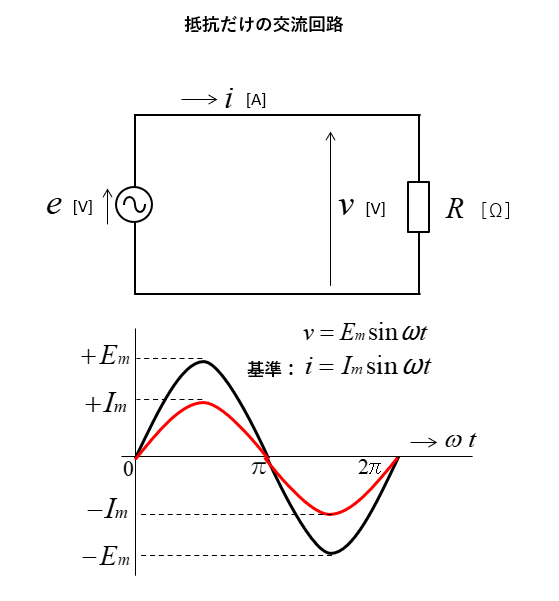
- \(e\cdots\)電源電圧
- \(v\cdots\)端子電圧
- \(i\cdots\)電流
- \(E_m\cdots\)最大値
- \(I_m\cdots\)最大値
電圧の瞬時値
抵抗 \(R\) の端子電圧 \(v\) は、電源電圧 \(e\) と等しくなります。
\(v=e=E_m\sinωt\)
\(v=e=\sqrt2E\sinωt\) [V]
\(E=\cfrac{E_m}{\sqrt{2}}\)
電流の瞬時値
抵抗 \(R\) に流れる電流の瞬時値は
\(i=I_m\sinωt\)
\(i=\sqrt2I\sinωt\) [A]
\(I=\cfrac{I_m}{\sqrt{2}}\)
電圧と電流の位相
\(v=E_m\sinωt\)
\(i=I_m\sinωt\) の式を
\(v=Ri\) に代入すると
\(E_m\sinωt=RI_m\sinωt\) になります。
\(t=0\) を代入すると
両辺が「0」になるので、位相差はなく「同相」になります。
\(e=\sqrt2E\sinωt\) [V]
\(i=\sqrt2I\sinωt\) [A]
抵抗だけの交流回路の、電圧と電流の位相は同相になる。
抵抗だけの交流回路の電圧と電流のベクトル図
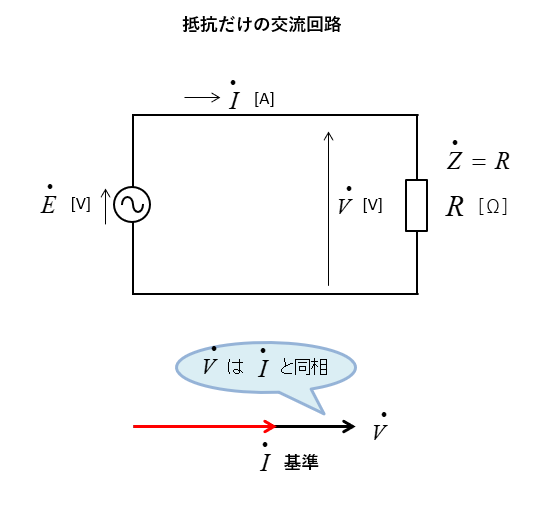
抵抗のインピーダンスは
\(\dot{Z}=R\)
回路に流れる電流 \(\dot{I}\) は
\(\dot{I}=\cfrac{\dot{V}}{R}\) なので
\(\dot{I}\) は \(\dot{V}\) と同相になります。
電圧と電流の大きさ(実効値)
電圧の実効値を \(V\) 、電流の実効値を \(I\) 、インピーダンスを \(Z=R\) とすると
オームの法則から
\(V=ZI\)
\(I=\cfrac{V}{Z}\)
\(Z=\cfrac{V}{I}\)
となります。
練習問題
問題1
図のような回路の抵抗 \(R=20\) [Ω] で交流電圧 \(v=100\sqrt2\sinωt\) [V] を加えたとき、回路に流れる電流 \(I\) の大きさを求めよ。
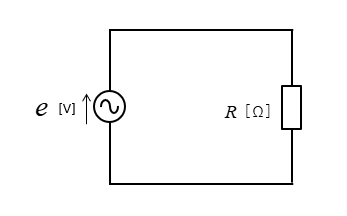
<解答例>
交流電圧の瞬時値 \(e\)、 実効値 \(E\) は
\(E=E_m\sqrt2、E_m=100\sqrt2\)
\(E=100\) [V]
電流 \(I\) は
\(I=\cfrac{E}{R}=\cfrac{100}{20}=5\) [A]
問題2
図のような回路において、抵抗 \(R=25\) [Ω]、 最大値 \(E_m=100\sqrt{2}\) [V] のときの電流 \(i\) [A] を求めよ。
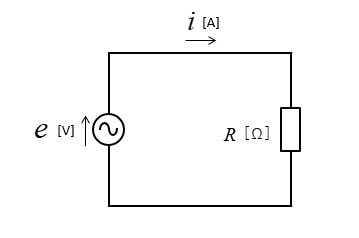
<解答例>
電源電圧 \(e=E_m\sinωt\) [V] から実効値 \(E\) を求めます。
\(E=\cfrac{E_m}{\sqrt2}=\cfrac{100\sqrt{2}}{\sqrt2}\)
\(E=100\) [V]
電流の実効値 \(I\) [A] は
\(I=\cfrac{E}{R}=\cfrac{100}{25}=4\) [A]
電流の瞬時値の式に \(I=4\) を入れると
\(i=\sqrt2×4\sinωt\)
\(i=4\sqrt2\sinωt\) [A] となります。
コイルだけの交流回路
コイルだけの交流回路の電圧と電流の瞬時値
コイル \(L\) だけの交流回路があります。

- \(e\cdots\)電源電圧
- \(v\cdots\)端子電圧
- \(i\cdots\)電流
- \(E_m\cdots\)最大値
- \(I_m\cdots\)最大値
電圧の瞬時値
コイル \(L\) の端子電圧 \(v\) は電源電圧 \(e\) と等しくなります。
\(v=e=E_m\sin(ωt+\cfrac{π}{2})\)
\(v=e=\sqrt2E\sin(ωt+\cfrac{π}{2})\) [V]
\(V=\cfrac{V_m}{\sqrt{2}}\)
電流の瞬時値
コイル \(L\) に流れる電流の瞬時値は
\(i=I_m\sinωt\)
\(i=\sqrt2I\sinωt\) [A]
\(I=\cfrac{I_m}{\sqrt{2}}\)
電圧と電流の位相
\(v=E_m\sin(ωt+\cfrac{π}{2})\)
\(i=I_m\sinωt\) の式を
\(v=Ri\) に代入すると
\(E_m\sin(ωt+\cfrac{π}{2})=RI_m\sinωt\) になります。
\(t=0\) の場合
電圧の値
\(v=E_m\sin\cfrac{π}{2}\)
電流の値
電流の値は、「0」になる。
したがって、電圧は電流より \(\cfrac{π}{2}\) 進む。
\(v=e=\sqrt2E\sin(ωt+\cfrac{π}{2})\) [V]
\(i=\sqrt2I\sinωt\) [A]
コイルだけの交流回路の、電圧は電流より \(\cfrac{π}{2}\) 進む。
コイルだけの交流回路の電圧と電流のベクトル図
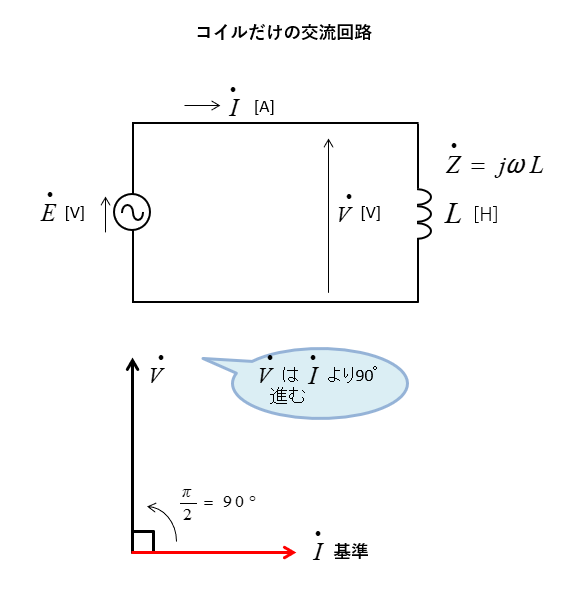
コイルのインピーダンスは
\(\dot{Z}=jωL\)
コイルの端子電圧 \(\dot{V}\) は
\(\dot{V}=jωL\dot{I}\) なので
\(\dot{V}\) は \(\dot{I}\) より \(\cfrac{π}{2}\) 進む。
電圧と電流の大きさ(実効値)
電圧の実効値を \(V\) 、電流の実効値を \(I\) 、インピーダンスを \(Z=ωL\) とすると
オームの法則から
\(V=ωLI\)
\(I=\cfrac{V}{ωL}\)
\(Z=\cfrac{V}{I}\)
となります。
練習問題
問題1
コイルの自己インダクタンス \(L=10\) [mH] のとき
周波数 \(50\) [Hz] における誘導リアクタンス \(X_L\) [Ω] を求めよ。
<解答例>
誘導性リアクタンス \(X_L=ωL=2πfL\) より
\(X_L=2π×50×10×10^{-3}=3.1415\) [Ω] になります。
問題2
インダクタンス \(L\) が \(100\) [mH] のコイルに \(50\) [Hz] 、\(100\) [V] の交流電圧を加えた場合の誘導リアクタンス \(X_L\) と電流 \(I\) を求めよ。
<解答例>
\(X_L=ωL=2πfL 、π=3.14\) とします。
\(X_L=2×3.14×50×100×10^{-3}\)
\(X_L=31.4\) [Ω]
\(I=\cfrac{E}{X_L}=\cfrac{100}{31.4}\)
\(I≒3.18\) [A]
問題3
\(e=150\sinωt\) [V] の交流電圧を加えたら、実効値 \(15\) [A] の電流が流れた。コイルの誘導リアクタンス \(X_L\) を求めよ。
<解答例>
\(e=E_m\sinωt\) より
電圧の最大値は \(150\) です。
電圧の実効値 \(E\) は
\(E=\cfrac{150}{\sqrt2}=75\sqrt2\) [V]
\(X_L=\cfrac{E}{I}=\cfrac{75\sqrt2}{15}=5\sqrt2\)
\(X_L≒7.07\) [Ω]
コンデンサだけの交流回路
コンデンサだけの交流回路の電圧と電流の瞬時値
コンデンサ \(C\) だけの交流回路があります。
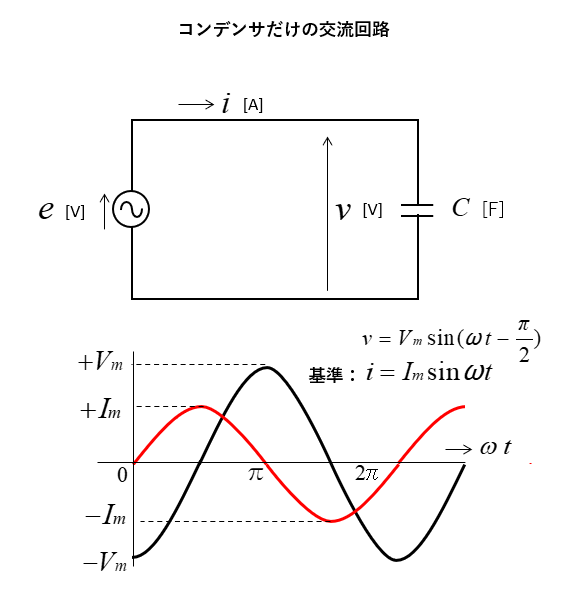
- \(e\cdots\)電源電圧
- \(v\cdots\)端子電圧
- \(i\cdots\)電流
- \(E_m\cdots\)最大値
- \(I_m\cdots\)最大値
電圧の瞬時値
コンデンサ \(C\) の端子電圧 \(v\) は電源電圧 \(e\) と等しくなります。
\(v=e=E_m\sin(ωt-\cfrac{π}{2})\)
\(v=e=\sqrt2E\sin(ωt-\cfrac{π}{2})\) [V]
\(V=\cfrac{V_m}{\sqrt{2}}\)
電流の瞬時値
コンデンサ \(C\) に流れる電流の瞬時値は
\(i=I_m\sinωt\)
\(i=\sqrt2I\sinωt\) [A]
\(I=\cfrac{I_m}{\sqrt{2}}\)
電圧と電流の位相
\(v=E_m\sin(ωt-\cfrac{π}{2})\)
\(i=I_m\sinωt\) の式を
\(v=Ri\) に代入すると
\(E_m\sin(ωt-\cfrac{π}{2})=I_m\sinωt\) になります。
\(t=0\) の場合
電圧の値
\(v=-E_m\sin\cfrac{π}{2}\)
電流の値
電流の値は、「0」になる。
したがって、電圧は電流より \(\cfrac{π}{2}\) 遅れる。
\(v=e=\sqrt2E\sin(ωt-\cfrac{π}{2})\) [V]
\(i=\sqrt2I\sinωt\) [A]
コンデンサだけの交流回路の、電圧は電流より \(\cfrac{π}{2}\) 遅れる。
コンデンサだけの交流回路の電圧と電流のベクトル図
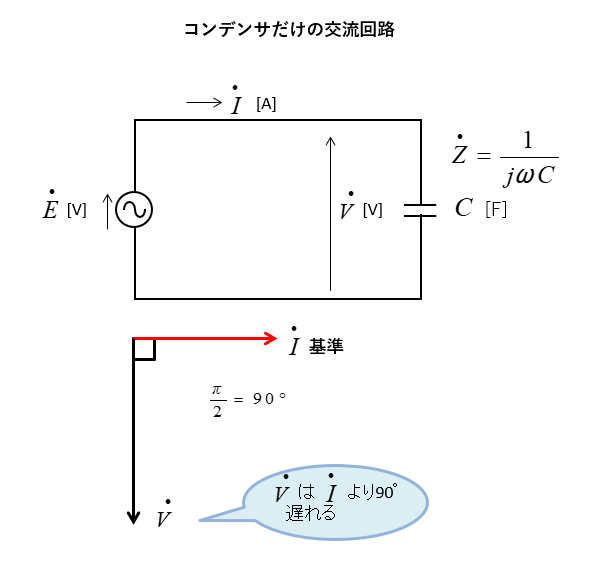
コンデンサのインピーダンスは
\(\dot{Z}=\cfrac{1}{jωC}\)
コンデンサの端子電圧 \(\dot{V}\) は
\(\dot{V}=\cfrac{\dot{I}}{jωC}=-j\cfrac{\dot{I}}{ωC}\) なので
\(\dot{V}\) は \(\dot{I}\) より \(\cfrac{π}{2}\) 遅れる。
電圧と電流の大きさ(実効値)
電圧の実効値を \(V\) 、電流の実効値を \(I\) 、インピーダンスを \(Z=\cfrac{1}{ωC}\) とすると
オームの法則から
\(V=\cfrac{I}{ωC}\)
\(I=ωCV\)
\(Z=\cfrac{V}{I}\)
となります。
虚数単位 \(j\) の付け方は、こちらが参考になります。
以上で「抵抗だけ・コイルだけ・コンデンサだけの交流回路」の説明を終わります。