抵抗とコイルの直列回路に、直流電源が接続されています。
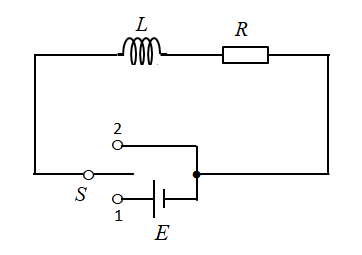
この回路において、スイッチを「1」に入れるとオームの法則によって、ある一定の大きさの電流が流れます。
ある一定の電流が流れるのはスイッチを入れてから、ある程度の時間が経過した後のことです。
ここでは、スイッチを入れた直後の過渡的な現象について説明します。
電源を入れた時の過渡現象
図のような「RL直列回路」に流れる、電流の過渡現象について考えてみます。
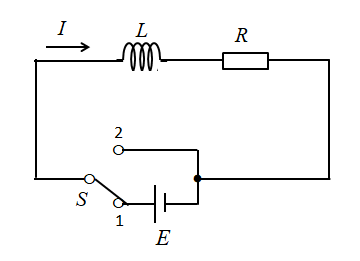
もし、コイルが無ければ電流 \(I\) は
\(I=\cfrac{E}{R}\) となります。
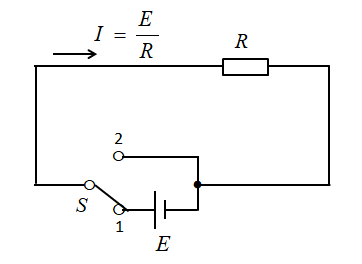
しかし、コイルがあるために、電流の流れを妨げる方向に起電力が発生します。
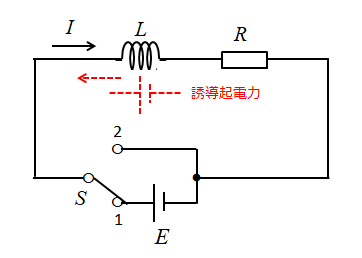
そのため、電流は徐々に大きくなって行き、最終的には
\(I=\cfrac{E}{R}\) の大きさになります。
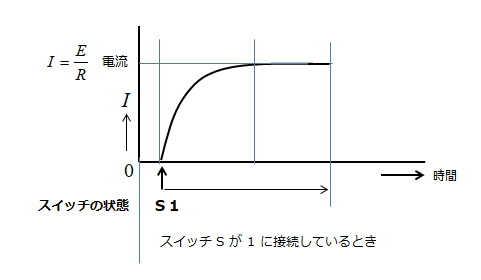
この時の電流を示している状態が下図の状態です。
コイル(インダクタンス)は、十分な時間が経過している(定常状態) では、短絡状態と同じ扱いになります。
電源を切った時の過渡現象
次に、スイッチを「2」に切り替えるとどうなるか見てみましょう。
ただし、スイッチが「1」から「2」に切り替わる時間は、十分に短いものとします。
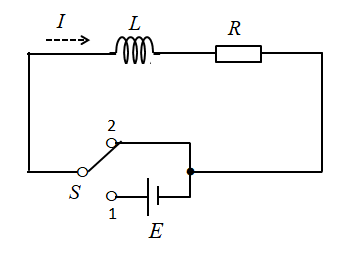
この場合も、もしコイルが無ければ電流 \(I\) は
\(I=0\) で単純です。
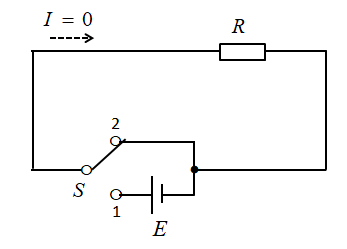
しかし、コイルがあるので
いままで流れていた電流 \(I\) を減らさないような起電力が発生するため、いきなり電流 \(I=0\) にはなりません。
最終的には、電流 \(I=0\) になります。
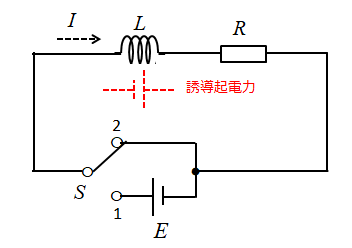
図の「S2」以後が、スイッチを「2」に切り替えた場合の電流の変化を示しています。
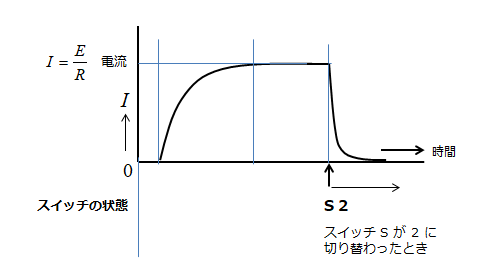
過渡現象の時の電流と起電力

RL直列回路の過渡現象
RL直列回路に流れる電流が変化すると、レンツの法則による誘導起電力が発生します。
スイッチを「1」にしたときの過渡現象
上図のRL直列回路で、スイッチを「1」に入れると、逆方向の起電力が発生します。
そのため、回路に流れる電流は徐々に大きくなって行きます。
そして、十分な時間が経過(定常状態)すると一定の大きさになります。
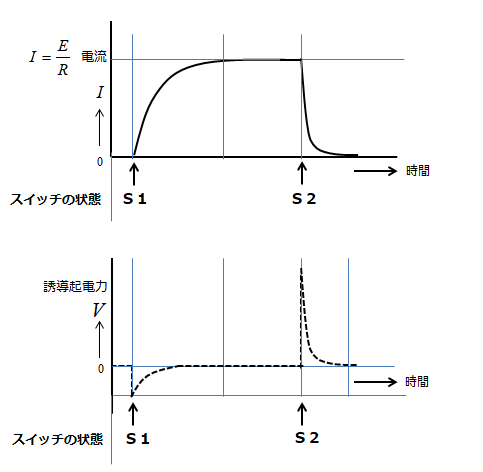
スイッチを「2」にしたときの過渡現象
ただし、スイッチが「1」から「2」に切り替わる時間は、十分に短いものとします。
RL直列回路で、スイッチを「1」から「2」にすると
図のような起電力が発生しますので、電流は徐々に小さくなります。
そして、十分な時間が経過(定常状態)するとゼロになります。
スイッチ「1」の時は、 徐々に電流が大きく なりますが、
スイッチ「2」の時は、流れている 電流が瞬時に切られる ため、電流の変化率が大きくなります。
したがって、スイッチ「2」のときの方がスイッチ「1」の時より、高い起電力が発生します。

以上で「抵抗とコイルの直列回路の過渡現象」の説明を終わります。