この記事で書いていること
抵抗は直流回路でも交流回路でも 電圧と電流の 位相 は同相になり位相がずれることはありません。
しかし、コイルとコンデンサの場合は交流回路では、電圧と電流の間に 位相差 がでてきます。
電圧と電流に位相差があるとき、電圧を基準にするか電流を基準にするかによって見方は反対になるので、よく理解していないとベクトル図などが描けません。
ここでは、コイルとコンデンサの位相の覚え方について説明します。
コイルの位相の覚え方
コイルは、\(E、L、I\)（エリー）と覚えます。
文字の順序が \(E\)（電圧）、\(L\)（コイル）、\(I\)（電流） となっているので 電圧が電流より進む と覚えます。
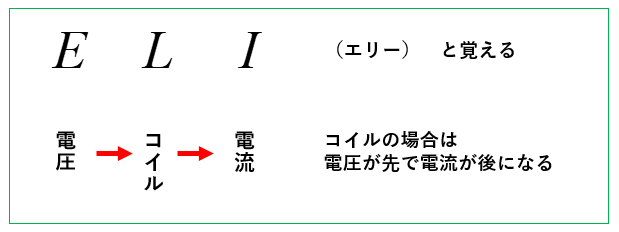
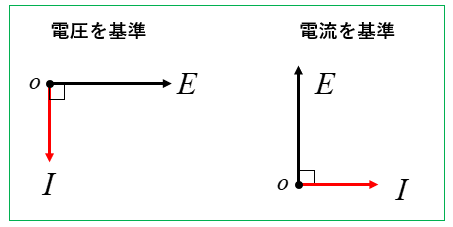
\(E、L、I\)（エリー）と覚えれば、電圧を基準にしても電流を基準にしても間違えません。
コンデンサの覚え方
コンデンサは、\(I、C、E\)（アイス）と覚えます。
文字の順序が \(I\)（電流）、\(C\)（コンデンサ）、\(E\)（電圧） となっているので 電流が電圧より進む と覚えます。
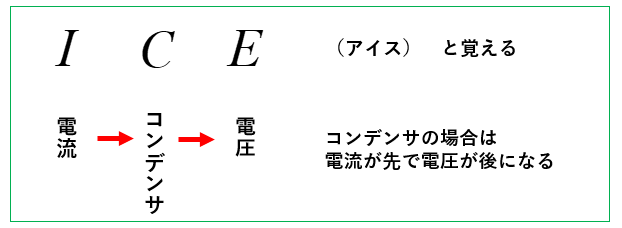
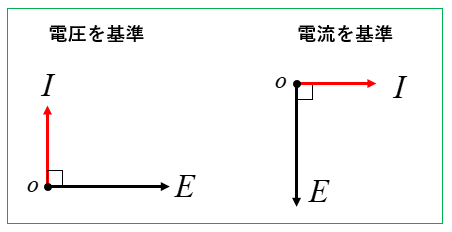
\(I、C、E\)（アイス）と覚えれば、電圧を基準にしても電流を基準にしても間違えません。
■ メモ
電圧と電流の進みと遅れについては、電圧を基準に考えるか、あるいは電流を基準に考えるかで違いますので、上のように覚えれば、どちらを基準にしても対応できると思います。
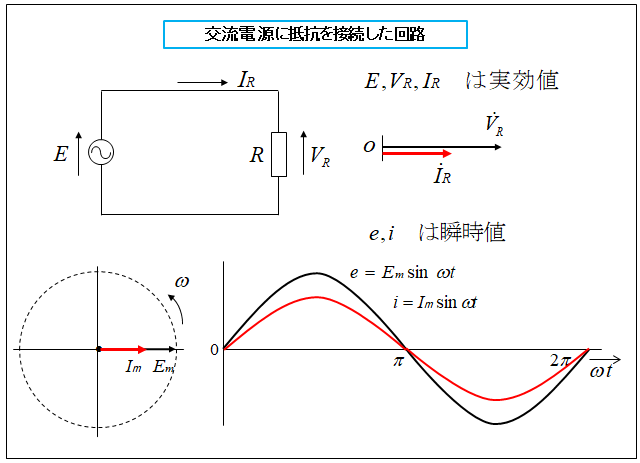
交流電源に抵抗を接続した場合
交流電源に抵抗を接続した場合は、電圧と電流の位相にズレ（位相差）はなく 同相 になります。
そのため、図に示すベクトルと波形になります。
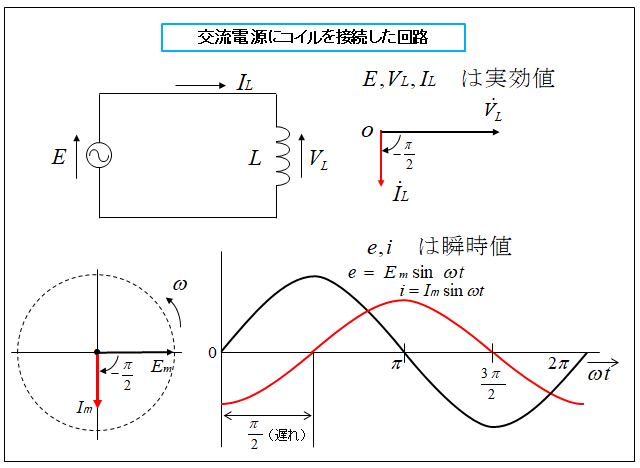
交流電源にコイルを接続した場合
交流電源にコイルを接続した時の、電圧と電流の関係を調べてみます。
コイルに加わる電圧とコイルを流れる電流の波形の間には
コイルの性質上 電流の波形は電圧の波形より \(\cfrac{π}{2}\) [rad] 遅れ ます。（電圧を基準にした場合）
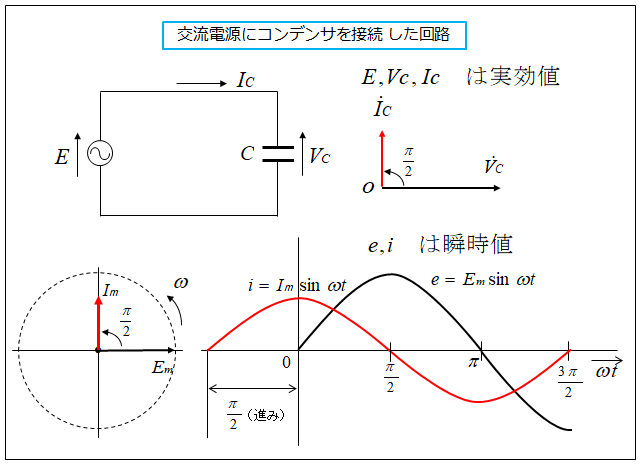
交流電源にコンデンサを接続した場合
交流電源にコンデンサを接続した時の、電圧と電流の関係を調べてみます。
コンデンサに加わる電圧とコンデンサを流れる電流の波形の間には、
コンデンサの性質上 電流の波形は電圧の波形より \(\cfrac{π}{2}\) [rad] 進み ます。（電圧を基準にした場合）
まとめ
■ コイルとコンデンサの位相の覚え方
電圧と電流どっちが先だっけ？
コイルの位相の覚え方
コイル\(\cdots ELI\)（エリー）と覚えましょう。
\(E\)（電圧）、\(L\)（コイル）、\(I\)（電流）の順なので、電圧が電流より進む。
コンデンサの位相の覚え方
コンデンサ\(\cdots ICE\)（アイス）と覚えましょう。
\(I\)（電流）、\(C\)（コンデンサ）、\(E\)（電圧）の順なので、電流が電圧より進む。
以上で「コイルとコンデンサの位相の覚え方」の説明を終わります。