角速度や角周波数は、1秒間に進む角度の大きさを「弧度法」で表示したものです。電気の分野では、角度を表示する場合に弧度法(ラジアン)を使います。
角速度はベクトル量、角周波数はスカラー量ですが、同じ用語で使われています。
ここでは、角速度と角周波数、弧度法の解説をします。
角速度 ω と 位相角 θ の関係

角速度 ω(オメガ)で、t 秒間移動した時の位相角 θ は、\(θ=ωt\) で表される。
- 弧度法の単位:1 [rad]
-
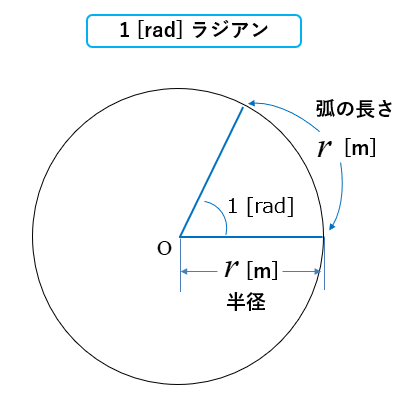
1 [rad] とは、「半径の長さ=弧の長さ」の時の中心角のこと。[rad] は弧度法の単位、読み方はラジアン。
半径の長さ=弧の長さ の時
\(1\) [rad]\(=\cfrac{弧の長さ}{半径}=\cfrac{r}{r}=1\)

- 角速度:1秒間に進む角度の大きさ
-
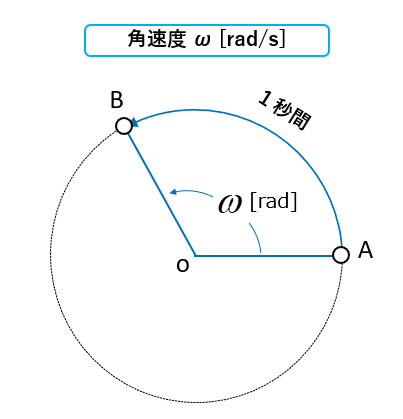
角速度とは、1秒間に A から B まで移動した時の角度の大きさを言う。
1秒間に ω [rad] 移動したとすれば、角速度は ω [rad/s] になります。
角速度の記号はω、単位は [rad/s] です。

- 角速度 ω と 位相角 θ の関係
-
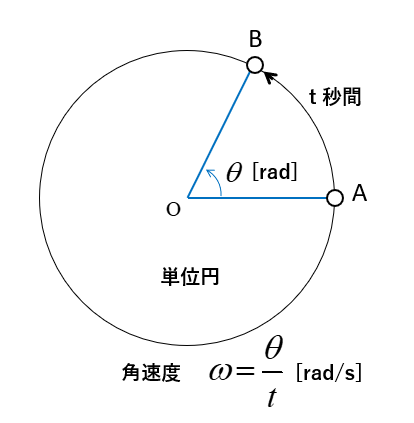
単位円において、t秒間に A から B まで θ [rad] 移動した時の角速度 ω [rad/s] は
\(ω=\cfrac{θ}{t}\) [rad/s]
\(θ=ωt\) [rad] になります。

角速度と各周波数
1回の円運動をする時間を「周期」、1秒間に回転する数が「周波数」 なので
周波数 \(f\) と周期 \(T\) の関係式は
\(f=\cfrac{1}{T}\) です。
1回転の角度は \(2π\) [rad]ですから、角速度は \(ω=2π\) です。
角速度を \(ω\)、周波数を \(f\) 、周期を \(T\) とすると、角速度 \(ω\) は 1秒間に \(f\) 回転することになります。
したがって
角周波数 \(ω=2πf=\cfrac{2π}{T}\) になります。
周波数については、次の記事が参考になります。
、周期を \(T\)
弧度法(ラジアン)と角度の変換
弧度法(ラジアン)を \(θ\)、度数を \(α\) とすると
\(θ=α×\cfrac{π}{180}\) [rad] の関係があります。
60度を弧度法(ラジアン)にすると、式に代入して
\(θ=60×\cfrac{π}{180}=\cfrac{π}{3}\) [rad]
■ よく使う角度
\(360°=2π\) [rad]
\(180°=π\)
\(90°=\cfrac{π}{2}\)
\(60°=\cfrac{π}{3}\)
\(45°=\cfrac{π}{4}\)
\(30°=\cfrac{π}{6}\)
交流電圧の角速度による表し方
\(\large e=E_m\sinθ\) [V]
\(\large e=E_m\sinωt\) [V]
\(\large e=E_m\sin2πft\) [V]
\(\large i=I_m\sinθ\) [A]
\(\large i=I_m\sinωt\) [A]
\(\large i=I_m\sin2πft\) [A]
まとめ
角速度や角周波数は、1秒間に進む角度の大きさを「弧度法」で表示したもの。角速度はベクトル量、角周波数はスカラー量ですが、同じ用語で使われます。
角速度 ω と 位相角 θ の関係
\(ω=\cfrac{θ}{t}\) [rad/s]
\(θ=ωt\) [rad] になります。
角周波数 \(ω=2πf=\cfrac{2π}{T}\) になります。
以上で「角速度と角周波数をわかりやすく解説!角速度と角周波数の違いは何?」の説明を終わります。