抵抗の並列回路では、回路に流れる電流がそれぞれの抵抗に 分流 されます。
流入する電流の和は流出する電流の和に等しい という キルヒホッフの第1法則 により
電流関係は
\(I=I_1+I_2\) になります。
分流の法則を、コンダクタンスを使って計算することができます。
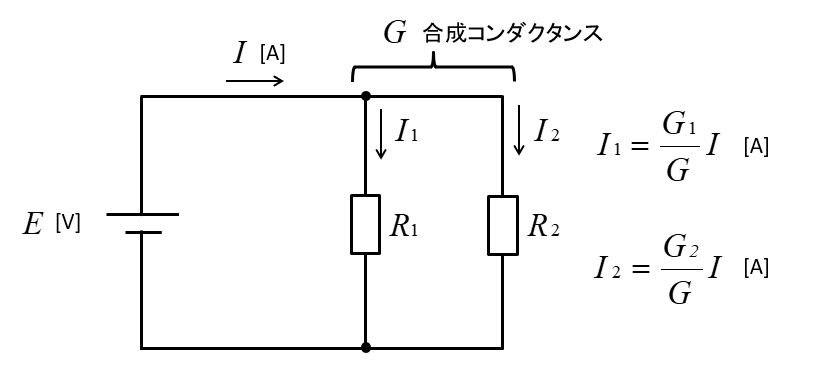
コンダクタンスに比例して、各枝路に電流が分流されます。
分流の法則をコンダクタンスで式にすると、次のようになります。

コンダクタンスによる分流の法則
分流の法則をコンダクタンスで式にすると、次のようになります。

コンダクタンスは、抵抗の逆数のことです。単位は [S](ジーメンス)
\(G_1=\cfrac{1}{R_1}\) [S]
\(G_2=\cfrac{1}{R_2}\) [S]
\(G_3=\cfrac{1}{R_3}\) [S]
合成コンダクタンスを \(G\) とすると
\(G=G_1+G_2+G_3\) [S]
コンダクタンスによる分流の法則(2個の抵抗の並列接続)
\(I_1=\cfrac{G_1}{G}I\) [A]
\(I_2=\cfrac{G_2}{G}I\) [A]
合成コンダクタンス
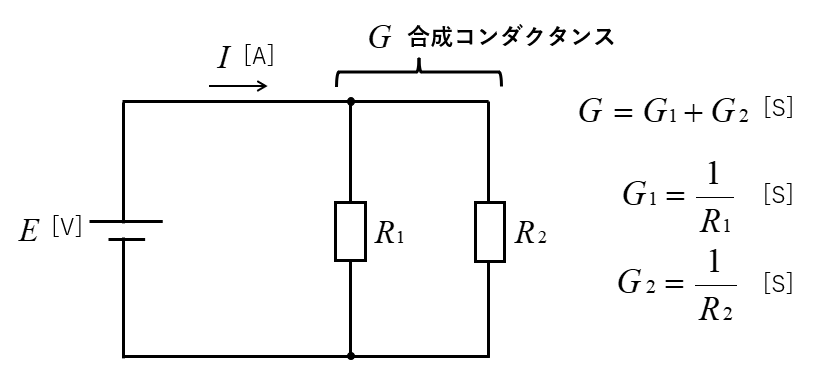
抵抗 \(R_1\)、\(R_2\) は、並列接続なので 合成コンダクタンス \(G\) は
\(G=G_1+G_2\) [S]
電源電圧
回路に流れる電流は \(I\) なので、電源電圧 \(E\) は
オームの法則から
\(E=RI=\cfrac{I}{G}\)
\(E=\cfrac{I}{G}=\cfrac{I_1}{G_1}=\cfrac{I_2}{G_2}\)
\(\cfrac{I}{G}=\cfrac{I_1}{G_1}\cdots(1)\)
\(\cfrac{I}{G}=\cfrac{I_2}{G_2}\cdots(2)\)
抵抗に分流される電流

抵抗 \(R_1\) に分流される電流 \(I_1\)
\(\cfrac{I}{G}=\cfrac{I_1}{G_1}\cdots(1)\) から
\(I_1=\cfrac{G_1}{G}I\)
抵抗 \(R_2\) に分流される電流 \(I_2\)
\(\cfrac{I}{G}=\cfrac{I_2}{G_2}\cdots(2)\) から
\(I_2=\cfrac{G_2}{G}I\) になります。
分流の法則をコンダクタンスで式にすると、次のようになります。

コンダクタンスによる分流の法則の例題(2個の抵抗の並列接続)
図のような回路において、抵抗に分流される電流 \(I_1\)、\(I_2\) を求めよ。
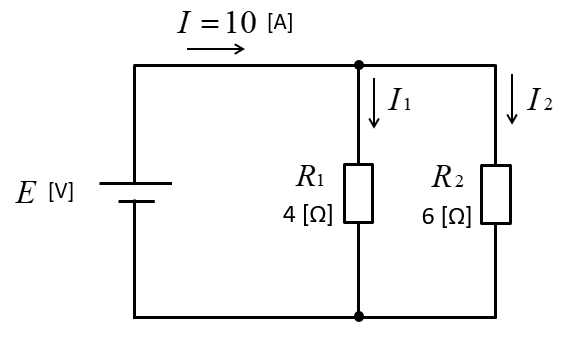
合成コンダクタンス
\(G=G_1+G_2\) [S]
\(G_1=\cfrac{1}{4}\)
\(G_2=\cfrac{1}{6}\)
\(G=\cfrac{1}{4}+\cfrac{1}{6}=\cfrac{10}{24}\)
回路に流れる電流
\(I=10\) [A]
コンダクタンスによる分流の法則の公式
\(I_1=\cfrac{G_1}{G}I\) [A]
\(I_2=\cfrac{G_2}{G}I\) [A]
分流の法則で計算すると
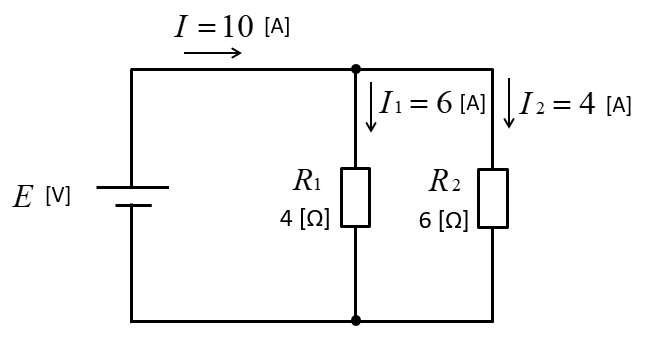
\(I_1=\cfrac{\cfrac{1}{4}}{\cfrac{10}{24}}×10=6\) [A]
\(I_2=\cfrac{\cfrac{1}{6}}{\cfrac{10}{24}}×10=4\) [A] になります。
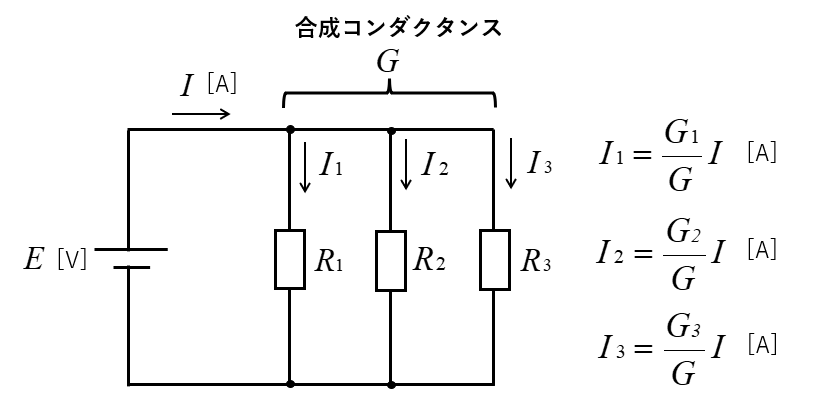
コンダクタンスによる分流の法則(3個の抵抗の並列接続)
\(I_1=\cfrac{G_1}{G}I\) [A]
\(I_2=\cfrac{G_2}{G}I\) [A]
\(I_3=\cfrac{G_3}{G}I\) [A]
合成コンダクタンス
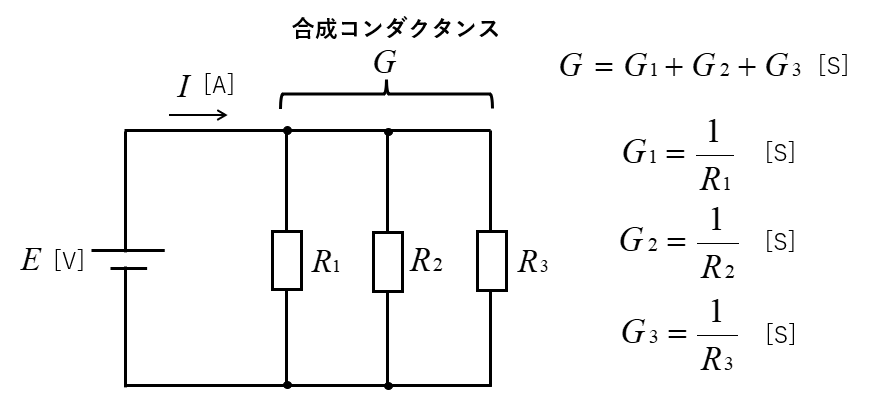
抵抗 \(R_1\)、\(R_2\)、\(R_3\) は、並列接続なので 合成コンダクタンス \(G\) は
\(G=G_1+G_2+G_3\) [S]
電源電圧
回路に流れる電流は \(I\) なので、電源電圧 \(E\) は
オームの法則から
\(E=RI=\cfrac{I}{G}\)
\(E=\cfrac{I}{G}=\cfrac{I_1}{G_1}=\cfrac{I_2}{G_2}=\cfrac{I_3}{G_3}\)
\(\cfrac{I}{G}=\cfrac{I_1}{G_1}\cdots(4)\)
\(\cfrac{I}{G}=\cfrac{I_2}{G_2}\cdots(5)\)
\(\cfrac{I}{G}=\cfrac{I_3}{G_3}\cdots(6)\)
抵抗に分流される電流
抵抗 \(R_1\) に分流される電流 \(I_1\)
\(\cfrac{I}{G}=\cfrac{I_1}{G_1}\cdots(4)\) から
\(I_1=\cfrac{G_1}{G}I\)
抵抗 \(R_2\) に分流される電流 \(I_2\)
\(\cfrac{I}{G}=\cfrac{I_2}{G_2}\cdots(5)\) から
\(I_2=\cfrac{G_2}{G}I\)
抵抗 \(R_3\) に分流される電流 \(I_3\)
\(\cfrac{I}{G}=\cfrac{I_3}{G_3}\cdots(6)\)
\(I_3=\cfrac{G_3}{G}I\) になります。
分流の法則をコンダクタンスで式にすると、次のようになります。

コンダクタンスによる分流の法則の例題(3個の抵抗の並列接続)
図のような回路において、抵抗に分流される電流 \(I_1\)、\(I_2\)、\(I_3\) を求めよ。
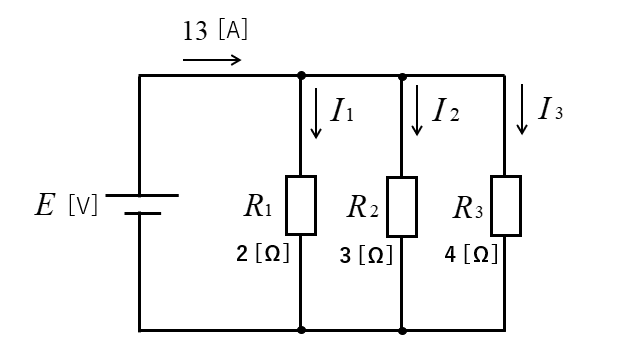
合成コンダクタンス
\(G=G_1+G_2+G_3\) [S]
\(G_1=\cfrac{1}{2}\)
\(G_2=\cfrac{1}{3}\)
\(G_2=\cfrac{1}{4}\)
\(G=\cfrac{1}{2}+\cfrac{1}{3}+\cfrac{1}{4}=\cfrac{13}{12}\)
回路に流れる電流
\(I=10\) [A]
コンダクタンスによる分流の法則の公式
\(I_1=\cfrac{G_1}{G}I\) [A]
\(I_2=\cfrac{G_2}{G}I\) [A]
\(I_3=\cfrac{G_3}{G}I\) [A]
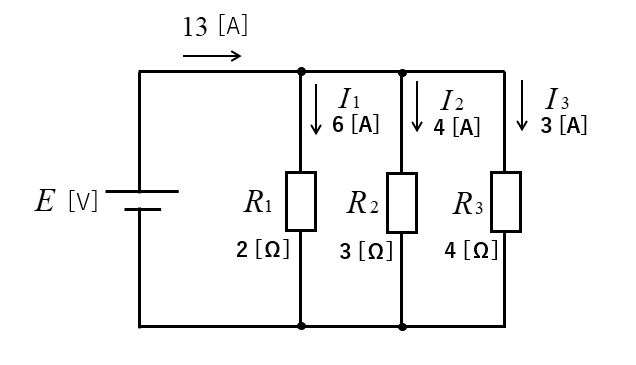
分流の法則で計算すると
\(I_1=\cfrac{\cfrac{1}{2}}{\cfrac{13}{12}}×13=6\) [A]
\(I_2=\cfrac{\cfrac{1}{3}}{\cfrac{13}{12}}×13=4\) [A]
\(I_3=\cfrac{\cfrac{1}{4}}{\cfrac{13}{12}}×13=3\) [A] になります。
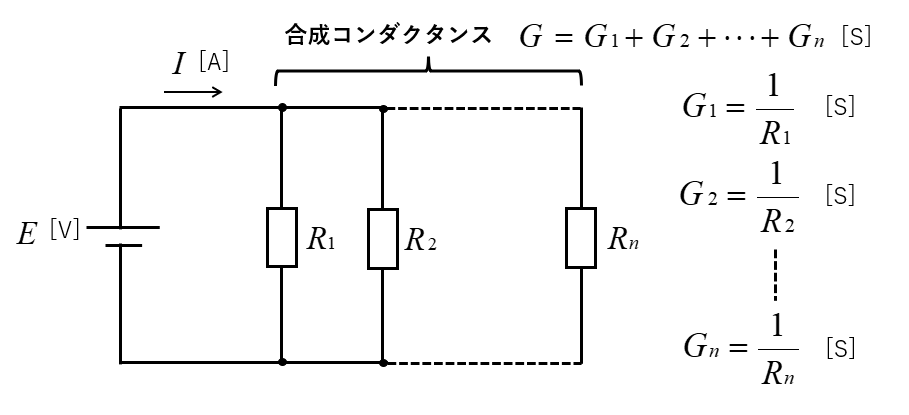
コンダクタンスによる分流の法則( \(n\) 個の抵抗の並列接続)
\(I_1=\cfrac{G_1}{G}I\) [A]
\(I_2=\cfrac{G_2}{G}I\) [A]
\(I_n=\cfrac{G_n}{G}I\) [A]
合成コンダクタンス
抵抗 \(R_1\)、\(R_2\)・・・\(R_n\) は、直列接続なので 合成コンダクタンス \(G\) は
\(G=G_1+G_2+\cdots+G_n\) [S]
電源電圧
回路に流れる電流は \(I\) なので、電源電圧 \(E\) は
オームの法則から
\(E=RI=\cfrac{I}{G}\)
\(E=\cfrac{I}{G}=\cfrac{I_1}{G_1}=\cfrac{I_2}{G_2}+\cdots+\cfrac{I_n}{G_n}\)
\(\cfrac{I}{G}=\cfrac{I_1}{G_1}\cdots(7)\)
\(\cfrac{I}{G}=\cfrac{I_2}{G_2}\cdots(8)\)
\(\cfrac{I}{G}=\cfrac{I_n}{G_n}\cdots(9)\)
抵抗に分流される電流
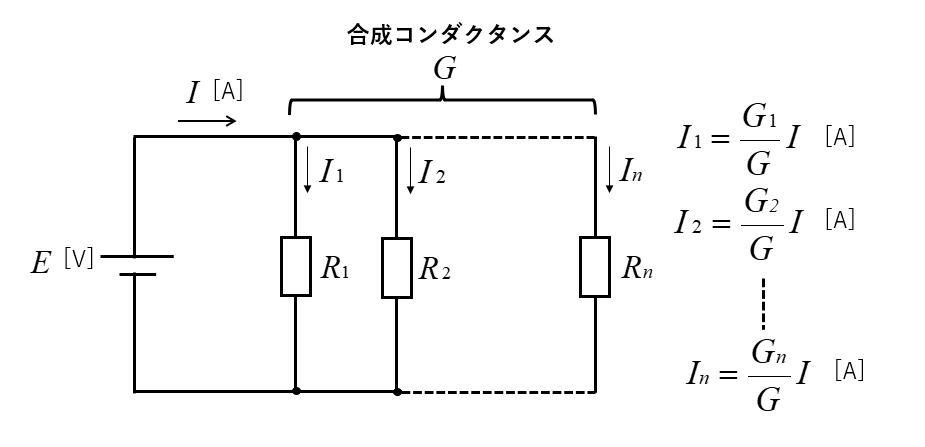
抵抗 \(R_1\) に分流される電流 \(I_1\)
\(\cfrac{I}{G}=\cfrac{I_1}{G_1}\cdots(7)\) から
\(I_1=\cfrac{G_1}{G}I\)
抵抗 \(R_2\) に分流される電流 \(I_2\)
\(\cfrac{I}{G}=\cfrac{I_2}{G_2}\cdots(8)\) から
\(I_2=\cfrac{G_2}{G}I\)
抵抗 \(R_n\) に分流される電流 \(I_n\)
\(\cfrac{I}{G}=\cfrac{I_n}{G_n}\cdots(9)\)
\(I_n=\cfrac{G_n}{G}I\) になります。
分流の法則をコンダクタンスで式にすると、次のようになります。
