電圧降下は抵抗の両端に電圧(電位差)が発生することです。抵抗などの負荷に電流が流れることで電圧降下が起こります。電流が流れない所では、電圧降下は起こりません。
電圧降下は、オームの法則で求めることができます。
抵抗の電圧降下と電圧降下の求め方

抵抗に電流が流れると、電流の入り口から出口に向かって電圧が下がります。これを電圧降下といいます。
図の回路の電圧の変化を示すと、青の線のように変化します。
- 電池の電圧により \(E\) [V] 電圧が上昇します。
- 抵抗に電流が流れることにより、\(RI\) [V] の電圧降下が起こります。
- キルヒホッフの第2法則により \(E=RI\) [V] になります。
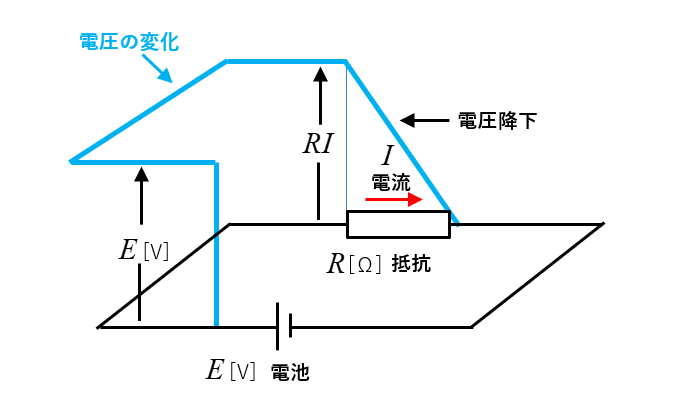
電圧降下の求め方
電圧降下は、抵抗に電流が流れることで起こります。したがって、電圧降下は、オームの法則から「抵抗×電流」で求めることができます。
抵抗を \(R\) [Ω]、電流を \(I\) [A] とすれば、オームの法則で
電圧降下=\(RI\) [V] で求められます。
電圧降下の問題
次の回路の各抵抗の両端の電圧を求めなさい。
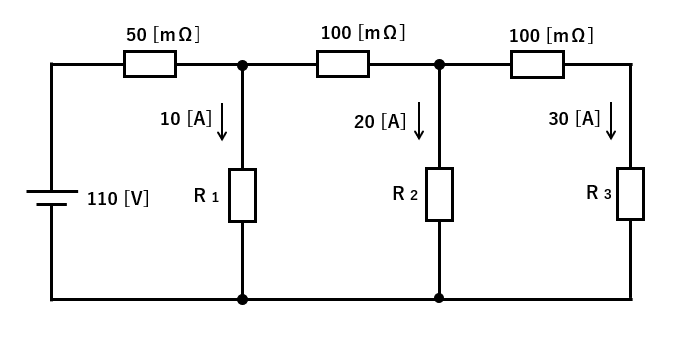
<解答例>
電池のマイナス側を基準にして、\(0\) [V] にして、\(a\) からの電圧降下を計算します。
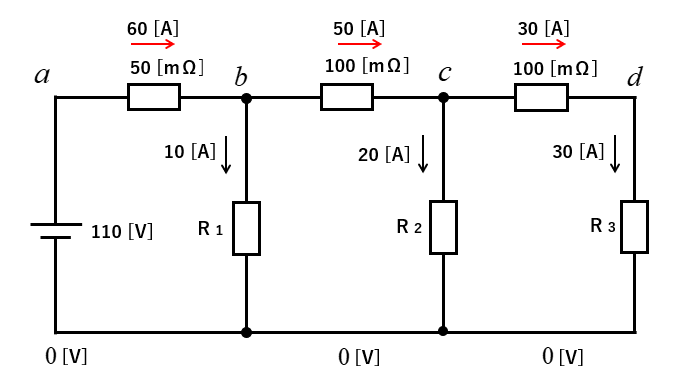
\(a\) の電位は、\(110\) [V]
\(ab\) 間の抵抗での電圧降下は、\(V_1=60×50×10^{-3}=3\) [V]
\(b\) の電位は、\(107\) [V]
\(bc\) 間の抵抗での電圧降下は、\(V_2=50×100×10^{-3}=5\) [V]
\(c\) の電位は、\(102\) [V]
\(cd\) 間の抵抗での電圧降下は、\(V_3=30×100×10^{-3}=3\) [V]
\(d\) の電位は、\(99\) [V]
したがって
\(R_1\) の両端の電圧は、\(107\) [V]
\(R_2\) の両端の電圧は、\(102\) [V]
\(R_3\) の両端の電圧は、\(99\) [V] になります。
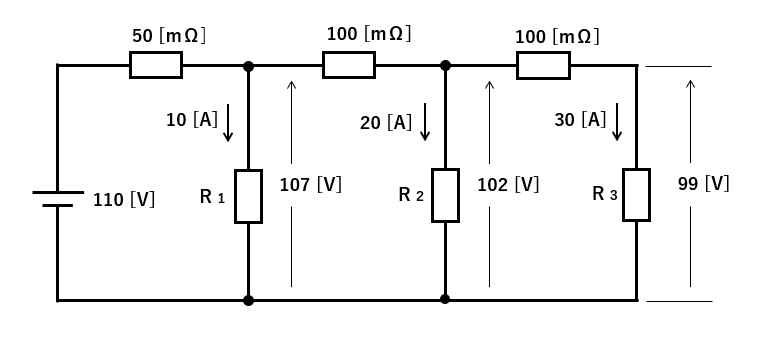
電圧降下から電流を求める問題
図のような4つの抵抗からなる回路があります。\(20\) [Ω] に流れる電流を求めよ。
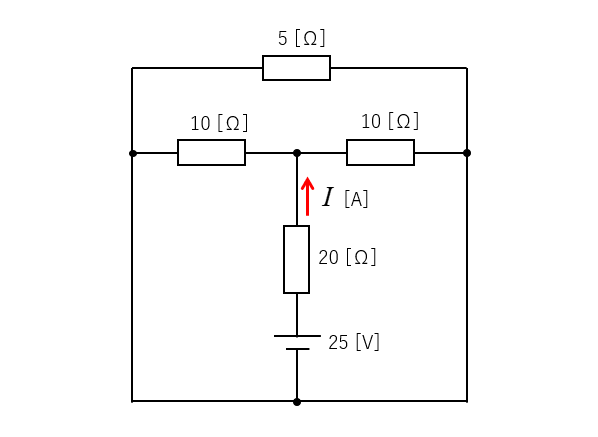
<解答例>
問題図を電位別に色分けをしてみると、図1のようになります。
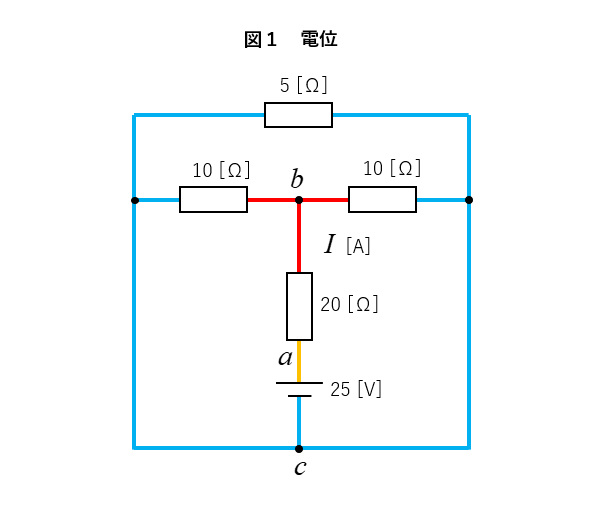
5[Ω] の抵抗の両端の電位は同じなので、電流は流れません。同じ電位の点は短絡または開放することができますので、図2のような等価回路にすることができます。
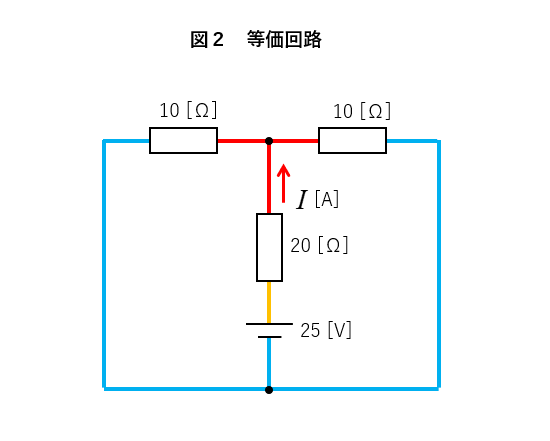
図2は抵抗の直並列接続の回路なので、図3のように変形できます。
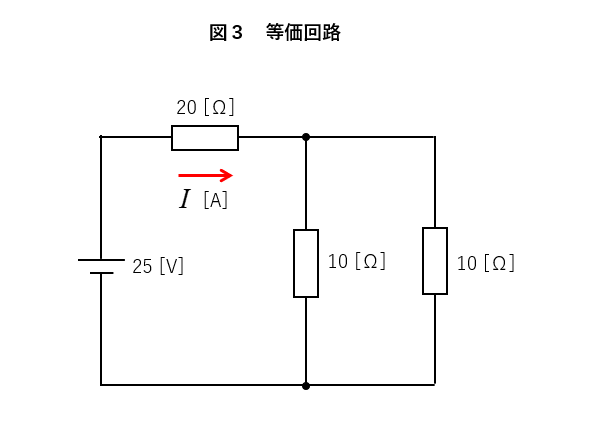
合成抵抗を \(R\) とすれば
\(R=20+\cfrac{100}{10+10}=25\) [Ω]
求める電流 \(I\) は、次のようになります。
\(I=\cfrac{E}{R}=\cfrac{25}{25}=1\) [A] になります。