電源とは、電気エネルギーを負荷に供給する装置のことで、電圧源と電流源があります。
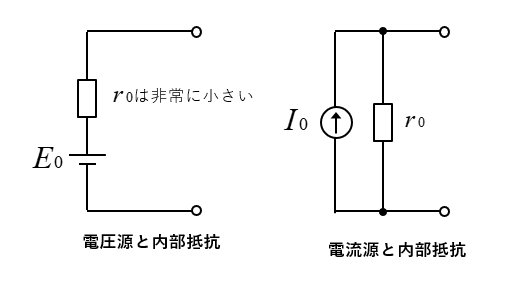
■ 電圧源とは
負荷の大きさが変動しても、一定の電圧 を供給できる電源のこと。
■ 電流源とは
負荷の大きさが変動しても、一定の電流 を供給できる電源のこと。
ここでは、電圧源と電流源の意味と 等価交換 について節米します。
電圧源と電流源の等価交換の公式
電圧源と電流源の間には、次の関係式があります。
電圧源を電流源に変換する
電圧源⇒電流源の変換式 \(I_0=\cfrac{E_0}{r_0}\) にして、\(r_0\) を電流源に並列に接続します。
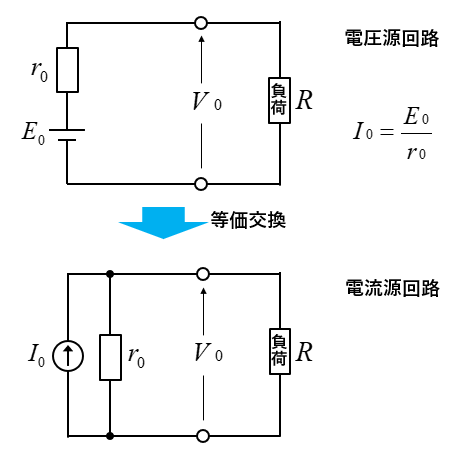
電流源を電圧源に変換する
電流源⇒電圧源の変換式 \(E_0=r_0I_0\) にして、\(r_0\) を電圧源に直列に接続します。
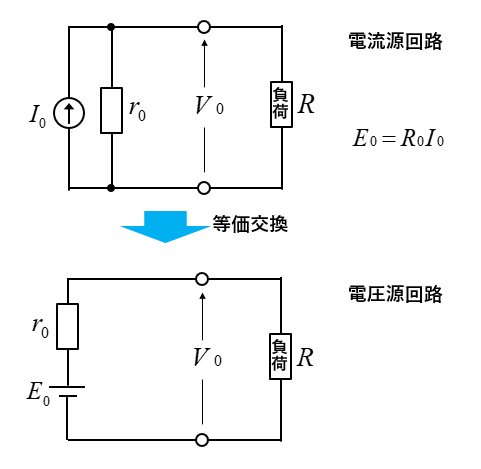
電圧源と電流源の等価回路の証明
電圧源と電流源が等価であるには、端子電圧と負荷電流が同じという条件が必要です。

電圧源 \(E_0=V_0+r_0I\cdots(1)\)
電流源 \(I=I_0-\cfrac{V_0}{r_0}\cdots(2)\)
式(1)に 式(2)を代入すると
\(E_0=V_0+r_0I=V_0+r_0\left(I_0-\cfrac{V_0}{r_0}\right)\)
\(E_0=V_0+r_0I_0-\cfrac{r_0V_0}{r_0}=r_0I_0\)
\(E_0=r_0I_0\) になり、等価交換の式になります。
以上のことから、電圧源と電流源を等価変換できる。
電圧源と電流源の内部抵抗について
電源というと電圧源が一般的で、電流源という考え方は普段の計算などではあまり使われないので馴染みがありません。
直流の電源としては、乾電池、バッテリー、小型で大きな容量のあるリチウム電池などがあります。
交流では家庭のコンセントに来ているものが、交流の代表といえます。
■ 電圧源の内部抵抗について
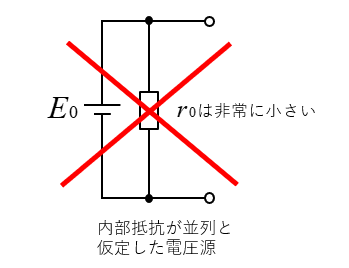
電圧源の内部抵抗は、理想的にはゼロが望ましいのですが、実際には非常に小さい抵抗があります。
そして、電圧源の内部抵抗は 直列 になっています。
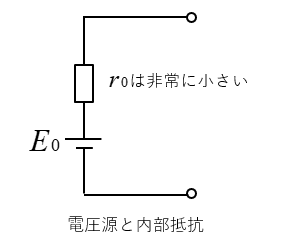
もしも、電圧源の非常に小さい内部抵抗が、並列に接続されていると短絡してしまいます。
■ 電流源の内部抵抗について
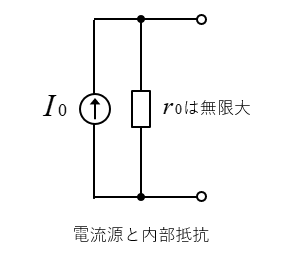
電流源の内部抵抗は、理想的には無限大です。
そして、電流源の内部抵抗は並列になっています。
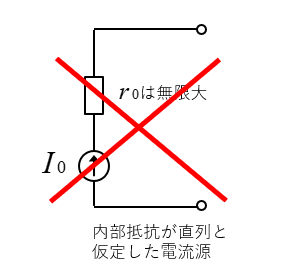
もしも、電流源の無限大の内部抵抗が、直列に接続されていると回路には電流が流れません。
定電圧源とは何か
一般的な電源では負荷の大きさが変動すると、電圧の大きさも変化します。
定電圧源は負荷の変動に関係なく常に一定の電圧を、供給する電源のことで 内部抵抗はゼロ と考えます。
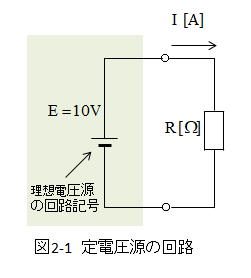
■ 定電圧源
- 理想的な電源を持つ、定電圧源です。
- この回路は電源電圧が \(10V\) の定電圧源です。
- 負荷として抵抗 \(R\) オームをつないであります。
- 定電圧源なので、内部抵抗はゼロです。
- 電源の電圧 E は常に一定で \(10V\) になります。
■ 抵抗 \(R\) の値を変化させた時の電流の変化の関係
- 定電圧源なので電圧は 10V で一定になります。
- オームの法則に従って、抵抗が小さくなると電流が大きくなります。
- 抵抗がどんどん小さくなってゼロに近づくと、電流は無限大になってしまう。
このような電源を定電圧源といいます。
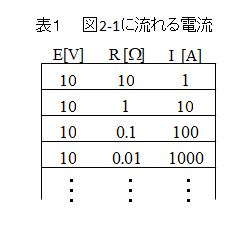
■ 抵抗と電流の関係をグラフで見る
- 抵抗が小さくなっていくと、電流は増加して行くことになります。
- 抵抗がゼロ(ショート)になると、流れる電流は無限大になります。
定電圧源では危険ですから、絶対に端子を短絡してはならない。
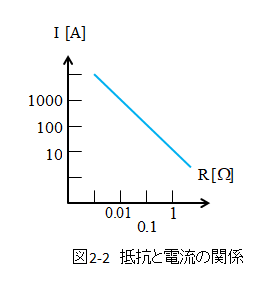
■ 定電圧電源の端子電圧
- 定電圧電源の端子電圧は内部抵抗による、電圧降下がないので常に一定になります。
- 電源電圧と端子電圧は等しくなります。
実際の電圧源の場合
- 実際の電源には少なからず、内部抵抗というものがあります。
そのため、電流が制限されるので無限大になることはありません。
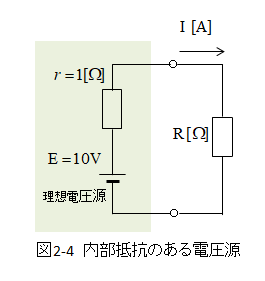
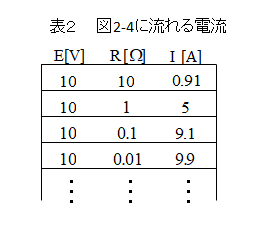
■ 内部抵抗のある電源の回路に流れる電流
- 負荷の抵抗と内部抵抗によって、回路に流れる電流が決まる。
- 負荷の抵抗がゼロ(ショート)になると電圧 10V、内部抵抗が1オームなのでオームの法則から電流は 10A になる。
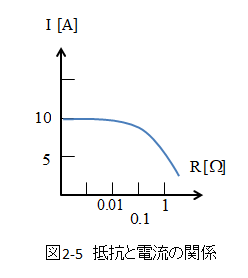
■ 抵抗と電流の関係をグラフで見る
- 負荷の抵抗がどんどん小さくなると、内部抵抗だけになる。
- そのため、回路を流れる電流は 10A に近づいて行くことになる。
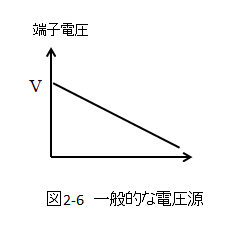
■ 一般的な電圧源の端子電圧
- 一般的な内部抵抗のある電圧源の場合
- 電流が流れると、内部抵抗で電圧降下がありますので端子電圧は変化する。
- 負荷の抵抗を小さくしていくと、短絡した時は端子電圧はゼロになる。
定電流源とは何か
負荷が変動しても常に一定の電流を供給する電源のことです。
定電流源では、内部抵抗は無限大 とされます。
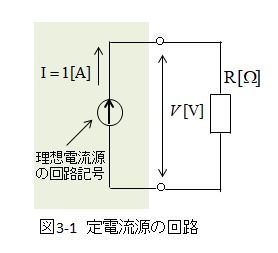
■ 定電流源
- 理想的な電源を持つ、定電流源です。
- この回路は 1A の電流が流れる定電流源です。
- 負荷に抵抗Rオームをつないであります。
- 定電流源なので、内部抵抗は無限大です。
- 回路に流れる電流は常に一定で1Aです。
- VはRにかかる両端の電圧です。
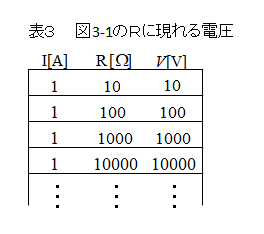
■ 表3は図3-1の抵抗Rの両端に現れる電圧の変化の関係
- 定電流源なので電流は1Aで一定です。
- オームの法則から、抵抗の大きさに比例して端子電圧 V は大きくなります。
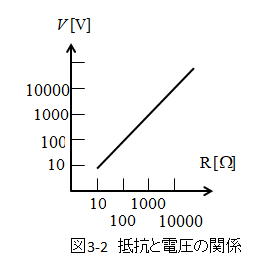
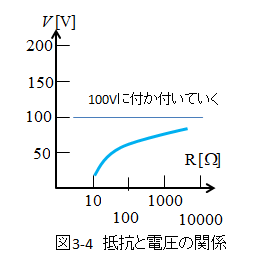
■ 抵抗と電圧の関係をグラフで見る
- 電流は1Aで一定なので、負荷にかかる電圧は抵抗に比例して変化します。
- そのため、どんどん抵抗が大きくなって無限大(端子が開放される)理論的には無限大の電圧になります。
定電流源では危険ですから端子を開放してはいけません。
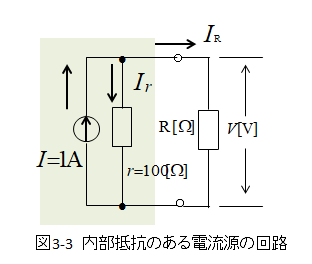
実際の電流源の場合
- 内部抵抗をもった電流源の回路です。
- 電流 I=1 A は \(I_R,I_r\) に分流します。
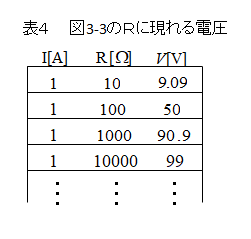
■ 表4は図3-3の抵抗Rの両端に現れる電圧の変化の関係
- 電流1Aを内部抵抗と負荷抵抗で分流されます。
- 負荷抵抗がどんどん大きくなっていくと、負荷抵抗に流れる電流はゼロに近くなります。
- その結果、電流 1A × 内部抵抗 100Ω で 100V に近づいていきます。
■ 抵抗と電圧の関係をグラフで見る
- 負荷抵抗が大きくなっていくと、オームの法則から内部抵抗と電流の積になり 100V に近づいていきます。
練習問題
問題1
図5-1 の \(I_3\) の値を求めよ。
この問題はキルヒホッフの法則の所で解いた問題です。解き方を比較してみてください。
図5-1を計算しやすいように変形する。
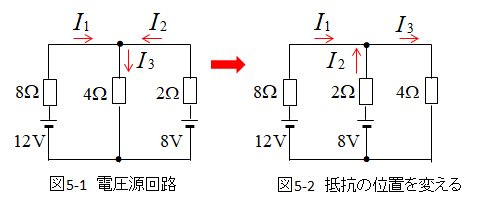
次に電流源の回路に置換して、回路を整理する。
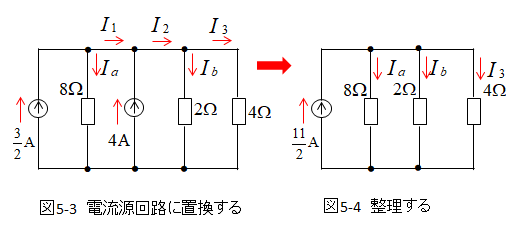
図5-3から
\(I_1=\cfrac{3}{2}A-I_a\)
\(I_2=4A-I_b\) となる。
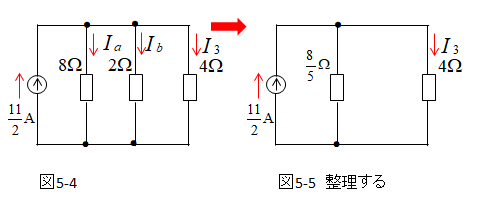
図5-4 は図5-5 のようにできるので
電流 \(\cfrac{11}{2}\) [A] が、抵抗の逆数に配分されるので \(I_3\) だけを求める問題ならば
\(I_3=\cfrac{11}{2}×\cfrac{1.6}{1.6+4}=\cfrac{11}{7}\) [A] のように計算できる。
さらに、\(I_1\) と \(I_2\) を求める必要がある場合は \(I_a\) と \(I_b\) を計算する。
手 順
1.合成抵抗の逆数を計算する。
2.並列抵抗に流れる電流は、抵抗の逆数に比例するということから配分する。
\(\cfrac{1}{R}=\cfrac{1}{8}+\cfrac{1}{2}+\cfrac{1}{4}=\cfrac{7}{8}\) [Ω]
\(I_a=\cfrac{11}{2}× \cfrac{\cfrac{1}{8}}{\cfrac{7}{8}}=\cfrac{11}{14}\) [A]
\(I_b=\cfrac{11}{2}× \cfrac{\cfrac{1}{2}}{\cfrac{7}{8}}=\cfrac{22}{7}\) [A]
\(I_1=\cfrac{3}{2}A-I_a=\cfrac{3}{2}A-\cfrac{11}{14}A=\cfrac{5}{7}\) [A]
\(I_2=4A-I_b=4A-\cfrac{22}{7}A=\cfrac{6}{7}\) [A] となります。