■ 定電圧源とは
負荷の大きさが変動しても、一定の電圧 を供給できる電源のこと。
■ 定電流源とは
負荷の大きさが変動しても、「一定の電流」を供給できる電源のことです。
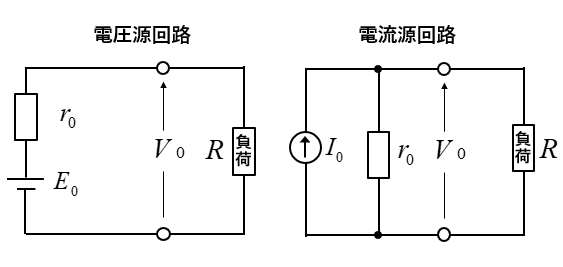
電源とは電気エネルギーを負荷に供給する装置のことで、電圧源と電流源 があります。
電源というと一般的には電圧源が使用されます。
ここでは定電圧源と定電流源の意味と等価交換について説明します。
定電圧源
電圧源の回路で負荷電流 \(I_L\) に関係なく、一定の端子電圧 \(V_L\) を出力する電源を 定電圧源 といいます。
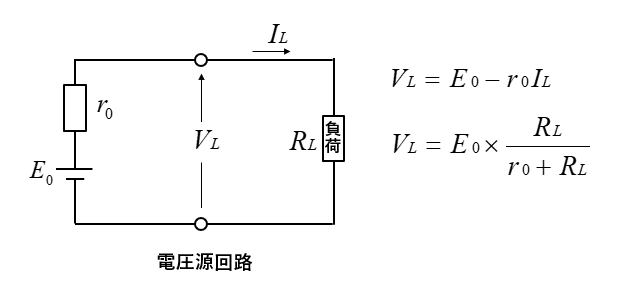
定電圧源では、内部抵抗 \(r_0=0\) なので、端子電圧 \(V_L\) は
\(V_L=E_0-r_0I_L=E_0\) になります。
実際の電圧源では内部抵抗 \(r_0\) がありますので \(V_L\) は
\(V_L=E_0-r_0I_L\)\(=E_0×\cfrac{R_L}{r_0+R_L}\) で表されます。
■ 定電圧源
一般的な電圧源は、内部抵抗 \(r_0\) が負荷抵抗 \(R_L\) に比べて
非常に小さいので(\(r_0 \ll R_L\))
\(V_L=E_0×\cfrac{R_L}{r_0+R_L}≒E_0\) と考えて、 定電圧源 として扱うことができます。
定電流源
電流源の回路で負荷抵抗 \(R_L\) に関係なく、一定の出力電流 \(I_L\) を出力する電源を 定電流源 といいます。
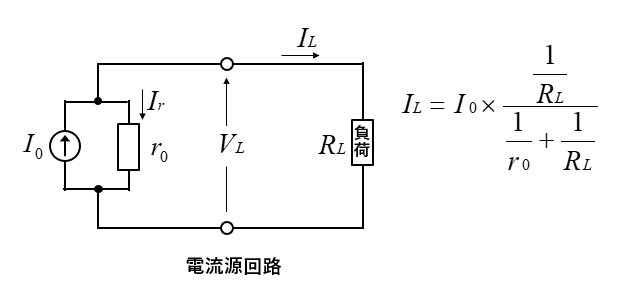
定電流源では、内部抵抗 \(r_0=∞\) なので、出力電流 \(I_L\) は
\(I_L=I_0-I_r=I_0\) になります。
実際の電流源では内部抵抗 \(r_0\) がありますので \(I_L\) は
\(I_L=I_0×\cfrac{\cfrac{1}{R_L}}{\cfrac{1}{r_0}+\cfrac{1}{R_L}}\) で表されます。
■ 定電流源
一般的な電流源は、内部抵抗 \(r_0\) が負荷抵抗 \(R_L\) に比べて
非常に大きいので(\(r_0 \gg R_L\))
\(I_L=I_0×\cfrac{\cfrac{1}{R_L}}{\cfrac{1}{r_0}+\cfrac{1}{R_L}}≒I_0\) と考えて、 定電流源 として扱うことができます。
電圧源と電流源の等価交換
電圧源 \(E_0\) と電流源 \(I_0\) の間には
\(I_0=\cfrac{E_0}{r_0}\) という関係があります。
この事により次のような、等価交換が成り立ちます。
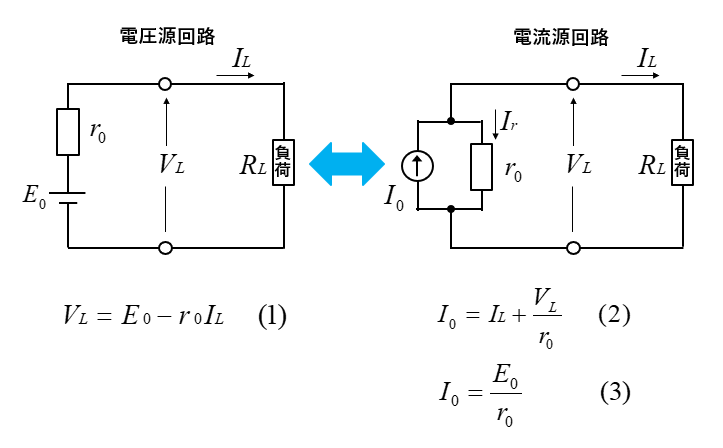
電圧源と電流源の等価交換は、次のように計算できます。
\(V_L=E_0-r_0I_L\cdots(1)\)
\(I_0=I_L+\cfrac{V_L}{r_0}\cdots(2)\)
式(1)を式(2)に代入する。
\(I_0=I_L+\cfrac{V_L}{r_0}\)\(=I_L+\cfrac{E_0-r_0I_L}{r_0}\)\(=\cfrac{E_0}{r_0}\)
\(I_0=\cfrac{E_0}{r_0}\) になります。
練習問題
問題1
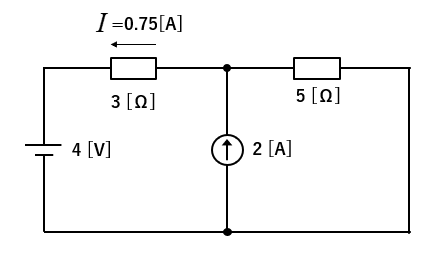
図の回路において、3Ωの抵抗に流れる電流 \(I\) を求めよ。
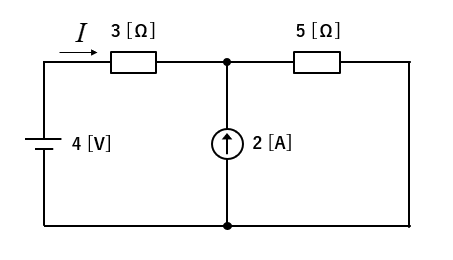
手順
「重ね合わせの理」を使って、電圧源の回路と電流源の回路に分けて考えます。
<解答例>
次のように、電圧源だけの回路と電流源だけの回路に分けます。
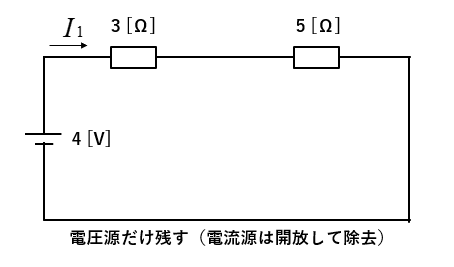
■ 電圧源だけの回路にする
電流源は \(0[A]\) で内部抵抗が無限大と想定し開放して除去します。
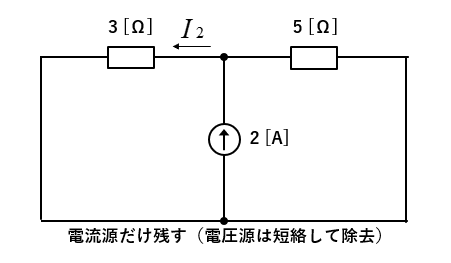
■ 電流源だけの回路にする
電圧源は \(0[V]\) で内部抵抗がゼロと想定し短絡し除去します。
計算すると
\(I_1=\cfrac{4}{3+5}=0.5\) [A]
\(I_2\) は並列接続になっているので、分流の法則から
\(I_2=2×\cfrac{5}{3+5}=1.25\) [A]
3Ωの抵抗に流れる電流 \(I\) は
\(I=I_1-I_2=0.5-1.25=-0.75\) [A] となります。
電流の符号が「マイナス」なので、向きは左向きになります。
問題2
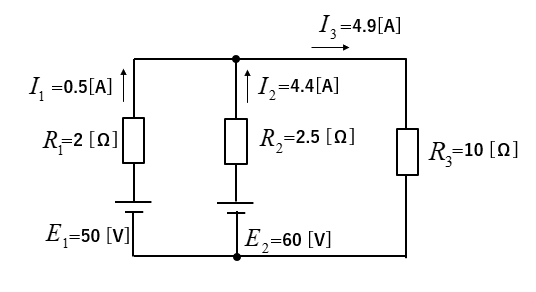
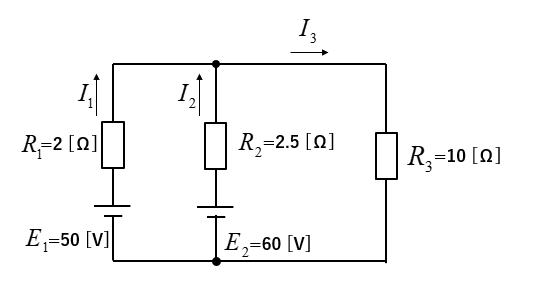
図の回路において、電圧源 \(E_1、E_2\) に流れる電流 \(I_1、I_2\) [A] と \(R_3\) に流れる電流 \(I_3\) [A] を求めよ。
<解答例>
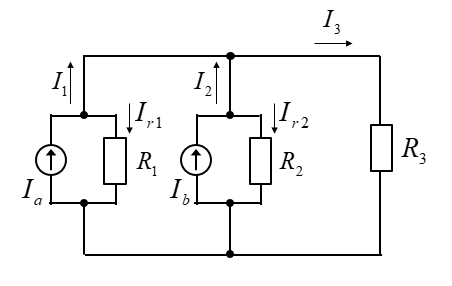
問題の回路を電流源の回路に等価交換します。
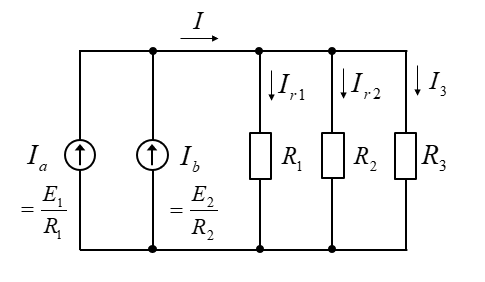
さらに整理すると次のようになります。
手順
\(I_a=\cfrac{E_1}{R_1}=\cfrac{50}{2}=25\) [A]
\(I_b=\cfrac{E_2}{R_2}=\cfrac{60}{2.5}=24\) [A]
\(I=I_a+I_b=49\) [A]
抵抗の並列回路の場合、各抵抗に流れる電流はコンダクタンスに比例します。
したがって、各枝路の電流 \(I_3、I_{r1}、I_{r2}\) は次のようになります。
\(I_3=I×\cfrac{1}{R_3}×\cfrac{1}{\cfrac{1}{R_1}+\cfrac{1}{R_2}+\cfrac{1}{R_3}}\)\(=49×\cfrac{1}{10}×\cfrac{1}{\cfrac{1}{2}+\cfrac{1}{2.5}+\cfrac{1}{10}}\)\(=4.9\) [A]
\(I_{r1}=I×\cfrac{1}{R_1}×\cfrac{1}{\cfrac{1}{R_1}+\cfrac{1}{R_2}+\cfrac{1}{R_3}}\)\(=49×\cfrac{1}{2}×\cfrac{1}{\cfrac{1}{2}+\cfrac{1}{2.5}+\cfrac{1}{10}}\)\(=24.5\) [A]
\(I_{r2}=I×\cfrac{1}{R_2}×\cfrac{1}{\cfrac{1}{R_1}+\cfrac{1}{R_2}+\cfrac{1}{R_3}}\)\(=49×\cfrac{1}{2.5}×\cfrac{1}{\cfrac{1}{2}+\cfrac{1}{2.5}+\cfrac{1}{10}}\)\(=19.6\) [A]
電圧源 \(E_1、E_2\) に流れる電流 \(I_1、I_2\) を求める。
\(I_1=I_a-I_{r1}\)
\(I_2=I_b-I_{r2}\)
\(I_1=I_a-I_{r1}=25-24.5=0.5\) [A]
\(I_2=I_b-I_{r2}=24-19.6=4.4\) [A]
結果
\(I_1=0.5\) [A]
\(I_2=4.4\) [A]
\(I_3=4.9\) [A]