合成抵抗の例題を集めました。
合成抵抗を求めるには、問題を解いてみることが理解する早道です。
実際に問題を解いて見ましょう。
例題合成抵抗の例題
例題1
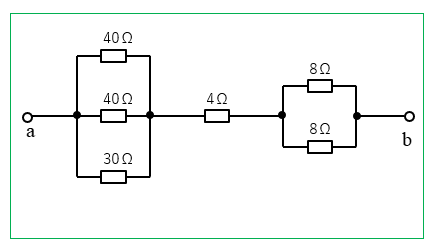
次のように抵抗が直列と並列に、複雑に接続されている場合の解き方を説明します。
<解答例>
解き方のコツは、並列に接続されている抵抗を1つに合成することです。
この問題は次のような順番で解いていきます。
1.回路を \(R_1、R_2、R_3\) に分けて考えます。\(R_1\) の回路には抵抗が3つありますので、2つだけの合成抵抗を求めます。
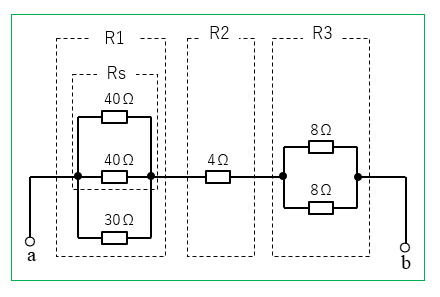
2.\(R_1\) の \(R_S\) から順に合成して単純にしていきます。
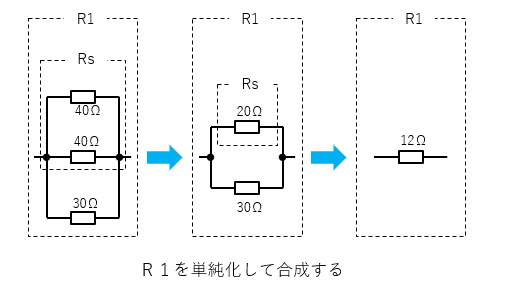
\(R_S\) を計算すると
\(R_S=\cfrac{40×40}{40+40}=20\quad\rm[Ω]\)
\(R_1\) を計算すると
\(R_1=\cfrac{20×30}{20+30}=12\) [Ω]
\(R_2=4\) [Ω]
\(R_3\) は並列接続ですから
\(R_3=\cfrac{8×8}{8+8}=4\) [Ω]
最後に \(R_1、R_2、R_3\) の直列接続になったので、足し算をすれば良いことになります。
合成抵抗\(=R1+R2+R3=12+4+4=20\) [Ω] となります。
合成抵抗の計算のコツ
並列抵抗を合成して単純化していくことが、計算をするときのコツになります。
例題2
オームの法則で合成抵抗を求めよ。
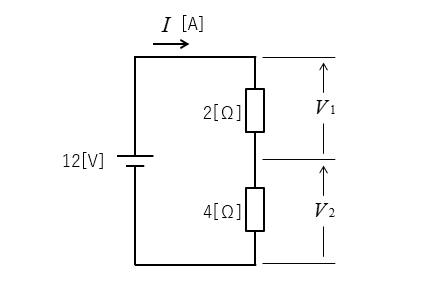
<解答例>
回路の合成抵抗を \(R\)、電圧を \(E\)、流れる電流 \(I\) とすると、各抵抗の端子電圧は
\(V_1=2×I\) [V]
\(V_2=4×I\) [V]
\(E=V_1+V_2\) ですから
\(12=2×I+4×I=6I=RI\) なので、オームの法則から \(E=RI\)
したがって、\(R=6\) [Ω] であることがわかります。
例題3
端子ab間の合成抵抗を求めよ。
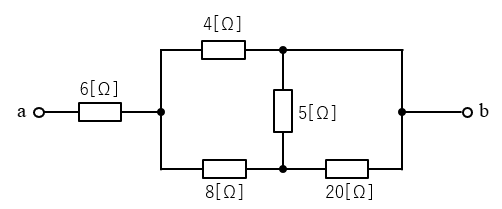
<解答例>
1.\(5\) [Ω] の抵抗の上端を右に移動すると、\(5\) [Ω] と\(20\) [Ω] の並列回路になります。
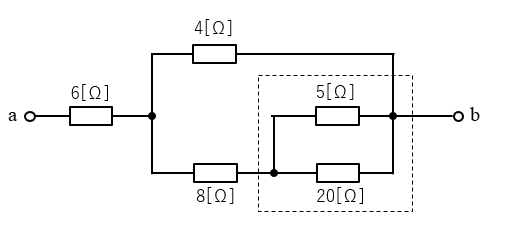
点線部分を「和分の積」で計算すると
合成抵抗は
\(\cfrac{5×20}{5+20}=4\) [Ω]
2.次に赤い点線部分は、\(8\) [Ω] と\(4\) [Ω] の直列回路になります。
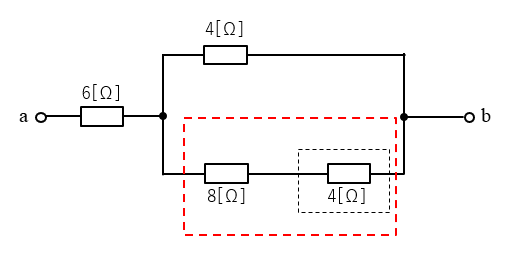
合成抵抗は
\(8+4=12\) [Ω]
3.次に緑の点線部分は、\(4\) [Ω] と\(12\) [Ω] の並列回路になります。
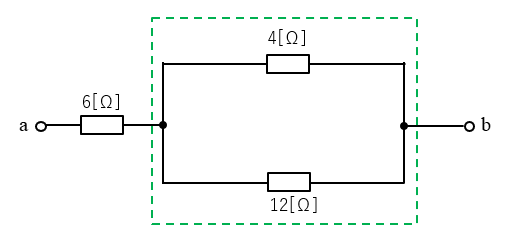
合成抵抗は
\(\cfrac{4×12}{4+12}=3\) [Ω]
4.最後は、\(6\) [Ω] と\(3\) [Ω] の直列回路になります。

ab間の合成抵抗は
\(6+3=9\) [Ω] になります。
例題4
図の回路の抵抗 \(R\) の両端の電圧が \(6\) [V]、電流 \(I\) が\(1\) [A] でした。
抵抗 \(R\) を求めよ。
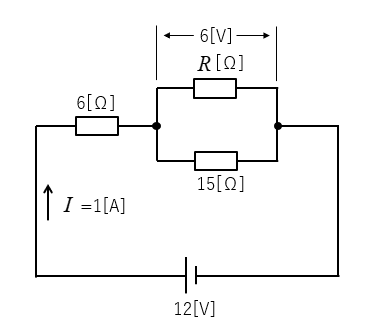
<解答例>
図のように抵抗に流れる電流を \(I_1、I_2\) として考えます。
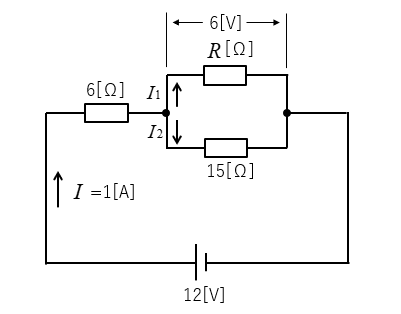
1.\(I_2\) は電圧と抵抗がわかっているので、オームの法則から
\(I_2=\cfrac{6}{15}=0.4\) [A]
2.回路を流れる電流 \(I=I_1+I_2\) なので
\(I_1=I-I_2=1-0.4=0.6\) [A] になります。
3.オームの法則から抵抗 \(R\) [Ω] は
\(R=\cfrac{E}{I}=\cfrac{6}{0.6}=10\) [Ω] になります。
例題5
端子ab間の合成抵抗を求めよ。

<解答例>
暗算でできそうな問題です。\(7.5\) [Ω] でOKと思ったら、\(2.5\) [Ω]
なんでー?
よく見たら、右側の \(5\) [Ω] は短絡されていた。確かに答えは \(2.5\) [Ω] でした。
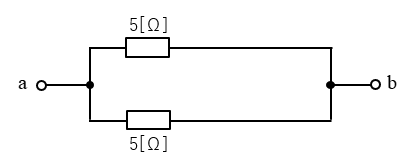
こんな問題もあるから注意が必要です。
答えは和分の積で求められます。
\(R=\cfrac{5×5}{5+5}=2.5\) [Ω]
例題6
端子ab間の合成抵抗を求めよ。
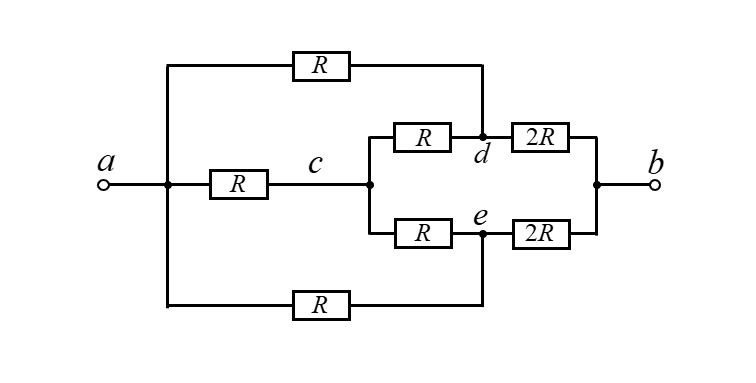
<解答例>
- 電流が a から b の方向に、流れると仮定します。
- ad と ae を見ると、対称になっているので d と e の電位は等しくなります。
- de 間の電位は等しいので、de 間を短絡できます。
電位が等しい時の「短絡または開放」については、ブリッジ回路とは の記事が参考になります。
問題の図は、次のように変形することができます。
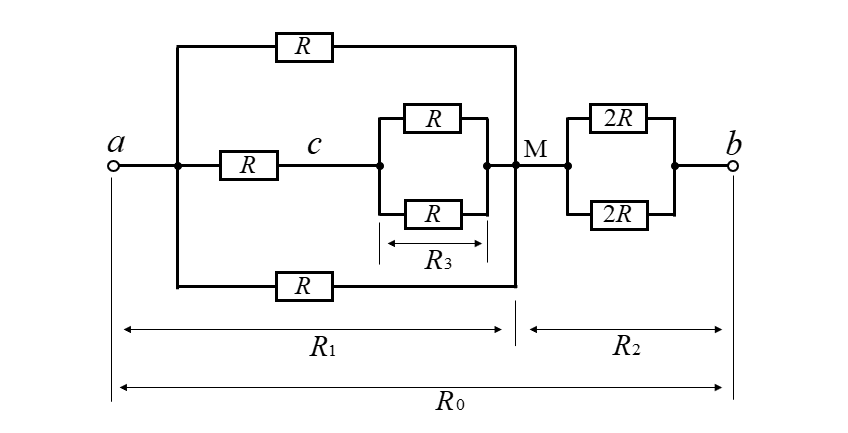
直並列接続の合成抵抗は、最も内部にある抵抗から求めていくのが定石です。
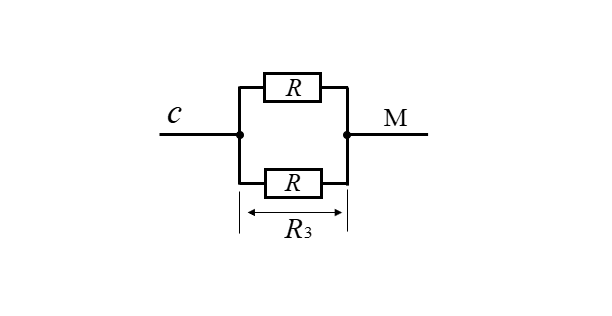
- cM 間の合成抵抗を \(R_3\)
- aM 間の合成抵抗を \(R_1\)
- Mb 間の合成抵抗を \(R_2\)
- ab 間の合成抵抗を \(R_0\) とすると
\(R_0=R_1+R_2\) になります。
- ■ 最も内部にある抵抗 \(R_3\) から求めます。
-

\(R_3\) は「和分の積」から
\(R_3=\cfrac{RR}{R+R}=\cfrac{R}{2}\) になります。
2つの並列接続された抵抗値が同じ場合は、\(\cfrac{1}{2}\) になることを知っていれば計算をしなくてもできます。
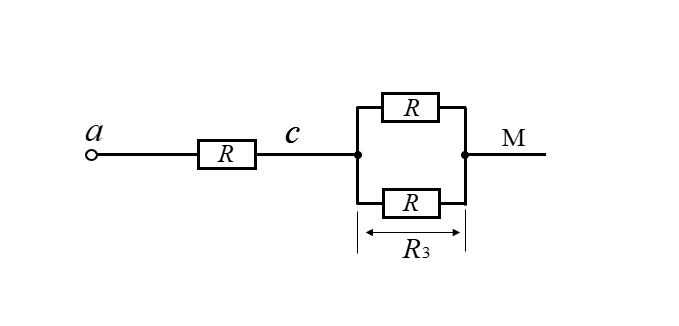
- ■ acM 間の抵抗は、直列接続です
-

acM 間の抵抗 \(R+\cfrac{R}{2}=\cfrac{3R}{2}\)
- ■ \(R_1\) は、\(R\) と \(\cfrac{3R}{2}\) と \(R\) の並列接続です
-

\(\cfrac{1}{R_1}=\cfrac{1}{R}+\cfrac{1}{\cfrac{3R}{2}}+\cfrac{1}{R}=\cfrac{8}{3R}\)
\(R_1=\cfrac{3R}{8}\)
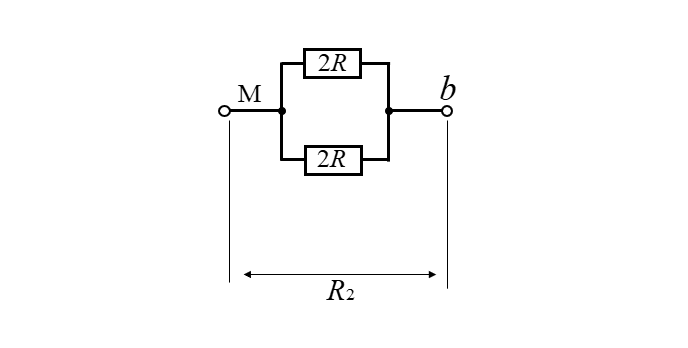
- ■ Mb 間の抵抗 \(R_2\) を求める
-

\(R_2=\cfrac{2R2R}{2R+2R}=R\)
- ab 間の合成抵抗 \(R_0\) を求める
-
\(R_0=R_1+R_2\) なので
\(R_0=\cfrac{3R}{8}+R\)
\(R_0=\cfrac{11R}{8}\) になります。
例題7
次の回路の合成抵抗を求め、回路に流れる電流 \(I\) [A] を求めよ。
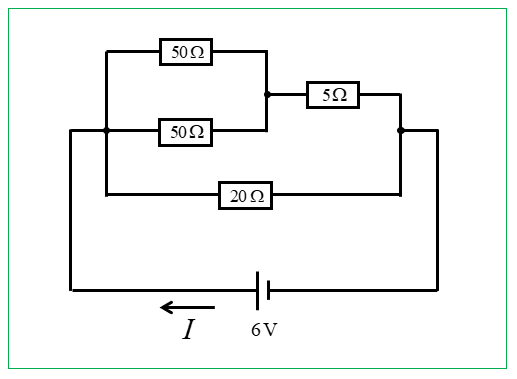
<解答例>
\(50と50\) [Ω] の並列接続なので \(25\) [Ω] になります。
\(25と5\) [Ω] の直列接続で \(30\) [Ω]
最後に \(30と20\) [Ω] の並列接続ですから和分の積を使って
合成抵抗\(=\cfrac{30×20}{30+20}=\cfrac{600}{50}\)
合成抵抗\(=12\) [Ω] になります。
回路に流れる電流 \(I\) は
\(I=\cfrac{E}{R}=\cfrac{6}{12}=0.5\) [Ω] になります。
例題8
図のような、直流回路に流れる電流 \(I\) [A] を求めよ。
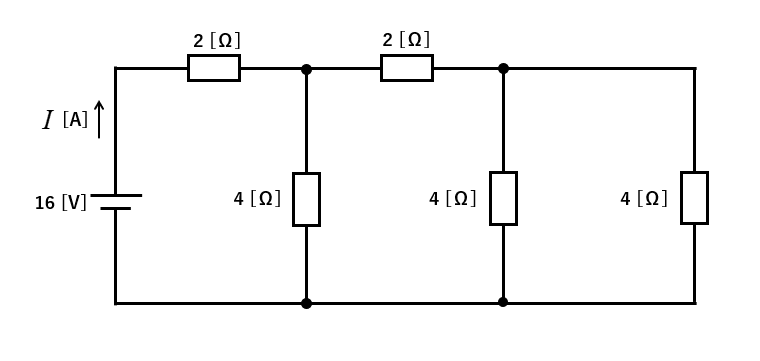
<解答例>
合成抵抗を求める場合の コツ は、一番うしろ(末端)の抵抗から計算することです。
問題の回路図を変形すると、次の図のようになります。
それぞれの抵抗に説明しやすいように、記号を付けます。
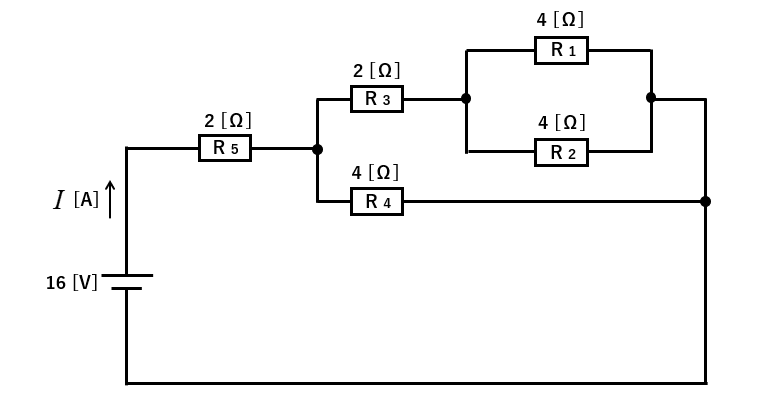
この回路で一番うしろの抵抗は R1とR2 ですから、この並列抵抗の合成を求めます。
2つの並列抵抗は「和分の積」で求められますが、並列接続の場合、2つの抵抗の大きさが同じときは 半分の大きさ になるということを知っておくと便利です。
R1とR2 の合成抵抗は \(2\) [Ω]
この合成抵抗 \(2\) [Ω] とR3 \(2\) [Ω] は直列ですから 足せば良いので \(4\) [Ω]
上の合成抵抗 \(4\) [Ω] とR4 \(4\) [Ω] は並列で 大きさが同じなので半分の \(2\) [Ω]
上の合成抵抗 \(2\) [Ω] とR5 \(2\) [Ω] は直列ですから 足せば良いので \(4\) [Ω] になります。
したがって、回路に流れる電流 \(I\) [A] はオームの法則から
\(I=\cfrac{16}{4}=4\) [A] になります。
この問題は合成抵抗の基本を理解していれば、簡単に解くことができる問題だと思います。
この問題は次のような問題にすることができます。
例題9
\(4\) [Ω] の抵抗に \(1\) [A] の電流が流れています。
回路に流れる電流 \(I\) [A] と電源電圧 \(E\) [V] を求めよ。
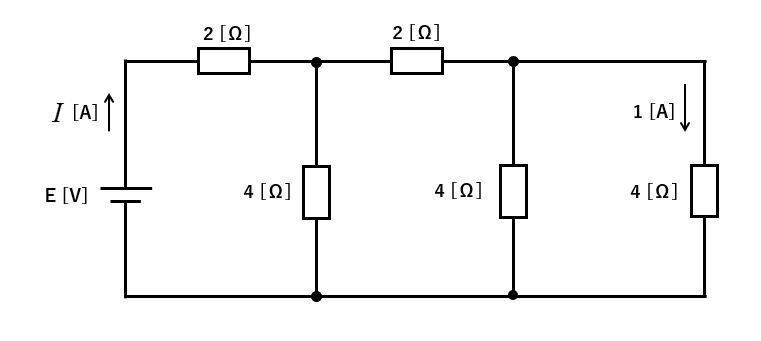
<解答例>
\(4\) [Ω] の抵抗の電圧降下は \(4\) [V] になりますので、\(a\)点の電圧は \(4\) [V] になります。
隣の \(4\) [Ω] に流れる電流 \(I_1\) は、オームの法則から \(1\) [A] であることがわかります。
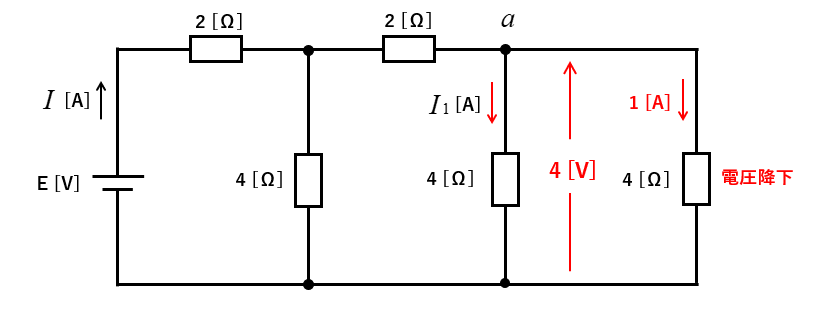
\(2\) [Ω] に流れる電流を \(I_2\) とすると、キルヒホッフの法則から
\(I_2=1+1=2\) [A] になります。
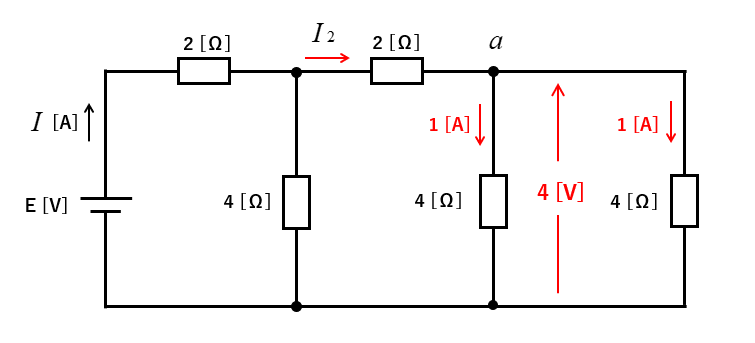
\(b\)点の電圧は \(8\) [V] なので \(I_2\) は \(2\) [A] になります。

回路に流れる電流 \(I\) は キルヒホッフの法則から \(4\) [A] になります。
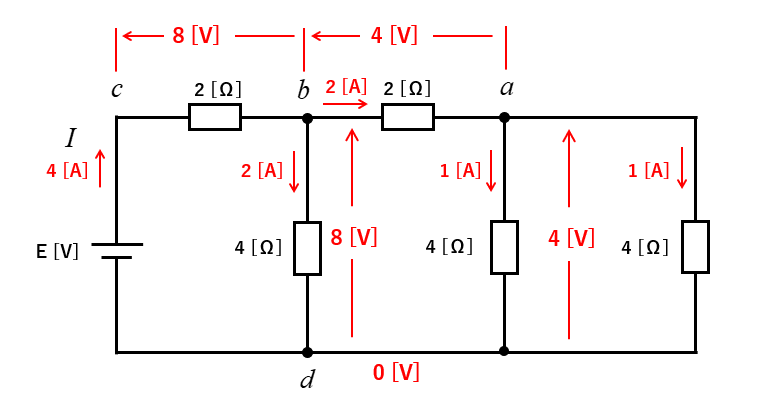
\(cbd\) 間の電圧が \(E\) になりますので
\(E=8+8=16\) [V] になります。