- 三相交流回路の計算をしてみます。
- スター結線の計算
- デルタ結線の計算
- 結線方式を変換する計算
について説明しています。
練習問題
三相交流回路 スター結線の計算
平衡三相交流回路の線間電圧が \(200\sqrt{3}\) [V] \(Z=4+j3\) [Ω] のとき
負荷に流れる電流を求めよ。
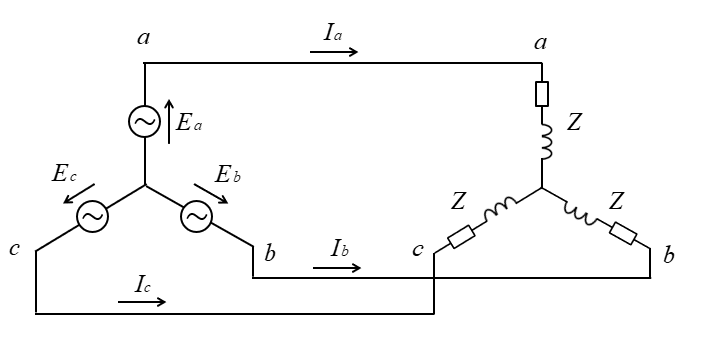
<解答例>
平衡三相交流回路なので相電圧 \(E_a、E_b、E_c\) を \(E_p\)
相電流 \(I_a、I_b、I_c\) を \(I_p\) とすると
各相に流れる電流は相電圧を各相のインピーダンスで割れば良いことになります。
スター結線の相電圧は公式から線間電圧の \(\cfrac{1}{\sqrt3}\) なので
\(E_p=\cfrac{200\sqrt{3}}{\sqrt{3}}=200\) [V] になります。
1相のインピーダンスは
\(Z=4+j3\) から
\(|Z|=\sqrt{4^2+3^2}=5\) [Ω]
負荷に流れる電流は
\(I_p=\cfrac{E_p}{Z}=\cfrac{200}{5}=40\) [A] となります。
三相交流回路デルタ結線の計算
平衡三相交流回路の線間電圧が \(200\sqrt{3}\) [V] \(Z=8+j6\) [Ω] のとき
回路に流れる線電流を求めよ。
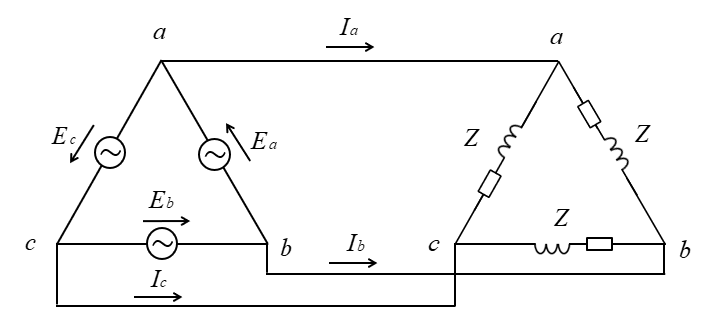
<解答例>
平衡三相交流回路なので相電流を \(I_p\)
相電圧 \(E_a、E_b、E_c\) を \(E_p\)
線電流 \(I_a、I_b、I_c\) を \(I_l\) とすると
デルタ結線の相電圧は線間電圧と等しいので \(E_p=200\sqrt3\) [V] になります。
1相のインピーダンスは
\(Z=8+j6\)から
\(|Z|=\sqrt{8^2+6^2}=10\) [Ω]
三相負荷に流れる相電流は
\(I_p=\cfrac{E_p}{Z}\)\(=\cfrac{200\sqrt3}{10}=20\sqrt3\) [A] となります。
デルタ結線の線電流は相電流を \(\sqrt3\) 倍 すれば良いので
\(I_l=20\sqrt3×\sqrt3=60\) [A] となります。
三相交流回路の変換式
平衡三相交流回路の電源の相電圧が \(200\) [V] \(Z=90+j30\) [Ω] のとき
回路流れる線電流を求めよ。
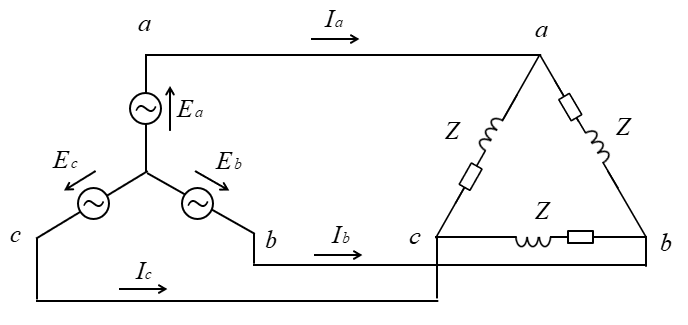
<解答例>
負荷側のデルタ結線をスター結線して、Y-Y結線に変換します。
スター結線に変換したインピーダンスを \(Z_Y\) とすると、次の図のようになります。
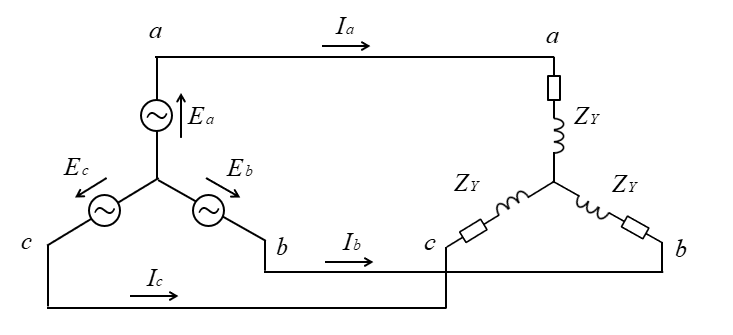
スター結線に変換したインピーダンス \(Z_Y\) はデルタ・スター変換公式より
\(Z_Y=\cfrac{Z}{3}=\cfrac{90+j30}{3}=30+j10\) [Ω]
\(|Z_Y|=\sqrt{30^2+10^2}=10\sqrt{10}\) [Ω]
負荷側をスターに変換したので 線電流=相電流ですから
\(I_L=\cfrac{200}{10\sqrt{10}}=2\sqrt{10}\) [Ω] になります。