数の意味
- 素数とは、1と自分以外の数では割り切れない数のことです。
たとえば、2,3,5,7,11,13,17…..などがあります。 - 自然数とは、正の整数のことです。0(ゼロ)や負の数は含まない。
- 整数とは、小数・分数でない数字のすべてのことで、0(ゼロ)も 負(マイナス)の数も含みます。
- 素因数分解とは、自然数(正の整数)を素数の積で表すこと。
- 有理数とは、分数で表せる数のこと。
a,bを整数(b≠0)とした時、\(\Large\frac{a}{b}\)の形で表せる数のこと。 - 無理数とは、分数で表せない数のこと。(例\(\sqrt2\)など)
a,bを整数(b≠0)とした時、\(\Large\frac{a}{b}\)の形で表せない数のこと。 - 最大公約数とは2つ以上の正の整数にに共通な約数(公約数)のうちの最大のもの。
- 最小公倍数とは2つ以上の正の整数にに共通な倍数(公倍数)のうちの最小のもの。
- 平方根とは「2乗するとaになる数}、つまり\(x^2=a\)で\(x\)のことを平方根という。
(例)9の平方根は \(3^2=9 、-3^2=9\)から\(±3\) となる - 展開と因数分解
展開とは\((x+a)(x+b) を(x^2+ax+bx+ab)\)のように分配法則でかっこを開くこと。
因数分解とは展開の逆をすること。 - 次数とは(項)に文字が掛けられている数をいう。\(3a^2\)は2次になる。
なぜなら、3×a×aで文字が2個掛けられている。 - ベクトルのあらわし方
\(\dot{A}\) - 虚数単位\((\sqrt{-1})\)は数学では( \(i\)) を使うが、電気工学では電流の記号に( \(i\)) を使うので、( \(j\)) を使う。
- スカラー・・・大きさのみを持つ量のことをいう。大きさと向きを持つ
ベクトルに対比する概念です。 - スカラー量・・・大きさのみ・長さ、質量、時間、温度、電荷、面積、体積、気圧、エネルギーなど。
- ベクトル量・・・大きさと向き・速度、加速度、力、運動量、角運動量、電流など。
有効数字について
有効数字とは、確実に信頼できる数字ことををいいます。
あるものの重さを測ったとき、3200 g ありました。
有効数字が、2桁のとき
確実に信頼できる数字は、「3 と 2」の数字です。
有効数字が、3桁のとき
確実に信頼できる数字は、「3 と 2 と 0」の数字です。
有効数字が、4桁のとき
確実に信頼できる数字は、「3 と 2 と 0 と 0」の数字です。
有効数字と桁数
■ 有効数字の表し方
有効数字は \(□×10^n\) で表します。
例えば、重さを測定したら \(3000\) g でした。
これを有効数字で表示すると、次のようになります。
有効数字1桁 \(\cdots 3×10^3\) g
有効数字2桁 \(\cdots 3.0×10^3\) g
有効数字3桁 \(\cdots 3.00×10^3\) g
有効数字4桁 \(\cdots 3.000×10^3\) g
同様に、重さが \(536,4\) kgの物があリます。
これを有効数字で表示すると、次のようになります。
有効数字1桁 \(\cdots 5×10^2\) kg
有効数字2桁 \(\cdots 5.3×10^2\) kg
有効数字3桁 \(\cdots 5.36×10^2\) kg
有効数字4桁 \(\cdots 5.364×10^2\) kg
\(15 \cdots\) 2桁
\(1.05 \cdots\) 3桁
\(0.036 \cdots\) 2桁 (位取りの「0.0」は有効数字にはならない。)
\(0.00506 \cdots\) 3桁 (位取りの「0.00」は有効数字にはならない。)
有効数字の加算と減算
■ 加 算
\(3.06 + 1.5\) の場合はどうなるのでしょうか?

最小の有効数字は、2桁です。
計算結果の \(4.56\) の数字の信頼できる数字は
\(4.5\) になりますので、\(4.56\) の \(0.06\) を四捨五入します。
その結果 \(4.6\) となります。
■ 減 算
\(3 – 0.02\) の場合はどうなるのでしょうか?

最小の有効数字は、1桁です。
計算結果の \(2.98\) の数字の信頼できる数字は
\(2\) になりますので、\(2.9\) の \(0.9\) を四捨五入します。
その結果 \(3\) となります。
有効数字の乗算と除算
■ 乗 算
\(2.34 × 1.1\) の場合はどうなるのでしょうか?
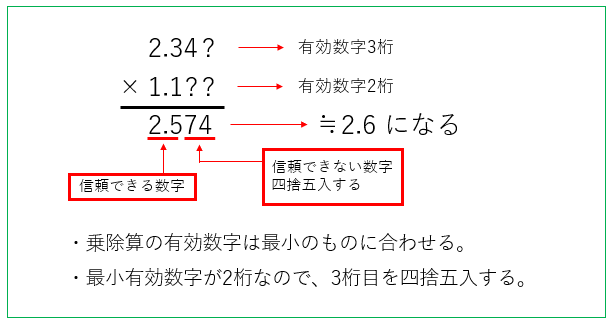
最小の有効数字は、2桁です。
計算結果の \(2.574\) の数字の信頼できる数字は
\(2.5\) になりますので、\(2.57\) の \(0.07\) を四捨五入します。
その結果 \(2.6\) となります。
■ 除 算
\(2.34 × 1.1\) の場合はどうなるのでしょうか?
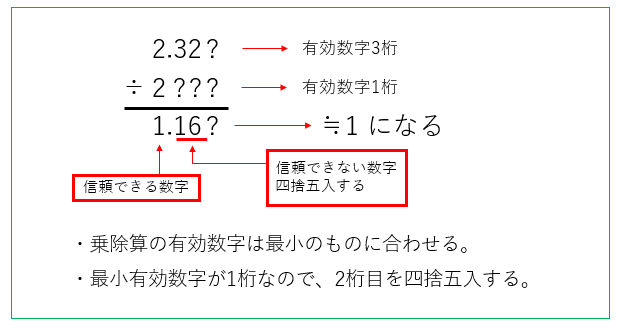
最小の有効数字は、1桁です。
計算結果の \(1.16\) の数字の信頼できる数字は
\(1\) になりますので、\(1.1\) の \(0.1\) を四捨五入します。
その結果 \(1\) となります。
有効数字の精度
■ 末尾につくゼロについて
\(12.3\) g と \(12.300\) g の精度の違い
\(12.3\) g の範囲は \(12.25~12.35\) g で \(0.1\) g の幅があります。
\(12.300\) g の範囲は \(12.2995~12.3005\) g で \(0.001\) g の幅があります。
したがって、\(12.3\) g と \(12.300\) g の精度は違います。
このことから、「末尾につくゼロは有効な数字の一部になる」ことがわかります。
■ 先頭につくゼロについて
\(0.001234\) kg と \(1.234\) g の精度について
\(0.001234\) kg の範囲は \(0.0012335~0.0012345\) kg で \(0.000001\) kg の幅があります。
\(0.000001\) kg\(=0.000001×1000\) g\(=0.001\) g になります。
\(1.234\) g の方は、\(1.2335~1.2345\) g で \(0.001\) g の幅があります。
したがって、\(0.001234\) kg と \(1.234\) g の精度は同じになります。
このことから、「先頭につくゼロは有効数字に関係しない」ことがわかります。
最大公約数と最小公倍数
最大公約数
2つ以上の正の整数に共通な約数(公約数)のうち最大のもの。
■ 共通に割れるだけ割る方法を使う場合
共通に割れる数の積が最大公約数になります。
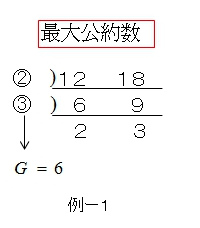
3つ以上の数のときも共通に割れる数の積が最大公約数になります。
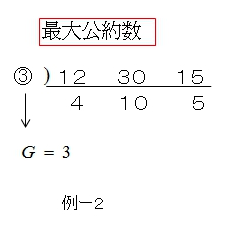
最小公倍数
2つ以上の正の整数に共通な倍数(公倍数)のうち最小のもの。
■ 共通に割れるだけ割る方法を使う場合
共通に割れる数と残った数の積が最小公倍数になります。

3つ以上の数のときは最小公倍数のやり方には注意が必要です。
共通に割るときに 一部でも割れるときは割り、他はそのまま残します。

不等号の意味
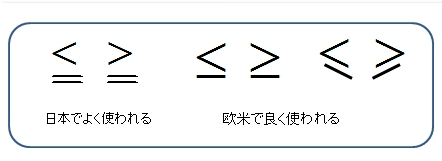
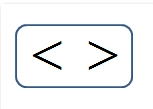
■ 「<」は左辺が右辺より小さいことを示す。
( a < b ) で a が b より小さいことを示す。
■ 「>」は左辺が右辺より大きいことを示す。
( a > b ) で a が b より大きいことを示す。
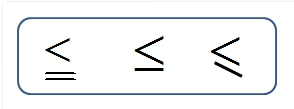
■ (すべて意味は同じ。)は左辺が右辺より小さいか等しい(a < b または a = b)ことを示す。
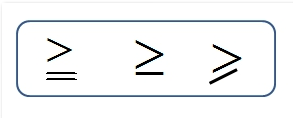
■ 左辺が右辺より大きいか等しい(a > b または a = b)ことを示す。

■ 右辺が左辺より非常に大きいことを示す。
あるいは、左辺が右辺より非常に小さいともいえる。

■ 左辺が右辺より非常に大きいことを示す。
あるいは、右辺が左辺より非常に小さいともいえる。
2次不等式
2次不等式の公式
\(ax^2+bx+c=0\) の解が \(x=α、β\) で \((β>α)\) のとき
\(ax^2+bx+c≧0 (a>0) → x≦α、 x≧β\)
\(ax^2+bx+c≦0 (a>0) → α≦x≦β\)
指数の意味を理解する
指数の役割りは何でしょうか?
もし、指数という考えがないとすると大変なことがあります。
たとえば 3を300回かけた計算式を書いてくださいという場合です。
3×3×3×3×3×3×3×3×3×3×3×3×3×3×…を繰り返さなければなりません。
べき乗という考えが出てきた
ここで登場したのが べき乗 というものです。
「べき乗」は簡単に言うと
同じ数を繰り返し掛けることを意味するものです。
たとえば、上の 「3を300回かけた計算式」 を表すには
次のように書けば良いのです。
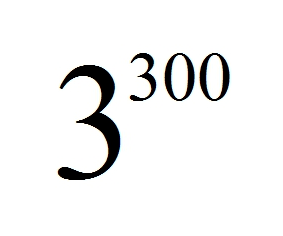
指数の意味
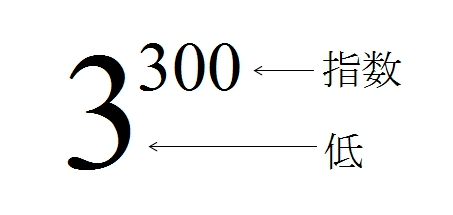
上に出てきた「掛け算を繰り返す回数」を 指数 といいます。
そして、この指数がついた数字を 低(てい) といいます。
つまり、上の 300 が 指数 で 3 が 低 となります。
■ 指数計算の考え方
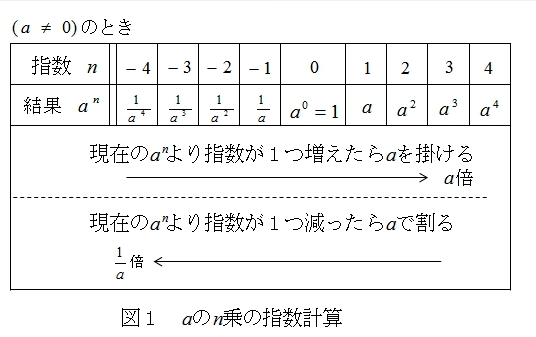
図1のように \(a^n\) の時
- 指数が増える時は a を掛ける。
- 指数が減る時は a で割る。と考えると都合が良い。
そのように考えると、 何かを「ゼロ乗」すると「1」になる 説明が付きます。
指数法則
■ \(a≠0\) で \(m,n\) が整数(正に限らない)のとき
- \(a^ma^n=a^{m+n}、a^{-m}=\cfrac{1}{a^m}\)
- \((a^m)^n=a^{mn}\)
- \((ab)^n=a^nb^n\)
整数とは、小数・分数でない数字のすべてのことで、0(ゼロ)も、負(マイナス)の数も含みます。
有理数と無理数
■ 有理数とは 分数で表せる数のこと。
\(有理数=\frac{b}{a}\)
\(a\) はゼロでないこと
■ 無理数とは 分数で表せない数のこと。
円周率の \(π\) や 平方根 \(\sqrt{2}\) などのことを無理数といいます。
平方根でも \(\sqrt{4}\) のように、根号がはずせるものは無理数ではありません。
無理数の四則計算
■ 無理数の足し算と引き算
無理数の計算のルール(足し算と引き算)は
「同じ無理数どうし」 でしか、足し算も引き算もできない。
\(\sqrt2、\sqrt3、\sqrt5、\)\(\sqrt6、\sqrt7、\sqrt{10}、\sqrt{11}\) などを、それぞれの文字と考えると良いでしょう。
それぞれを a、b、c、dなどのように考えると、文字が違うのでそのまま単純に足したり、引いたりできません。
\(3\sqrt2\) というのは \(\sqrt2+\sqrt2+\sqrt2\) のことです。
つまり、\(\sqrt2\) が 3つ あるということです。
■ 例題 足し算・引き算
\(3\sqrt2+\sqrt2=4\sqrt2\) で \(\sqrt2\) を文字と考えた場合 \(3a+a=4a\) と同じと考えることができます。
\(8\sqrt5-4\sqrt5=4\sqrt5\) で \(\sqrt5\) を文字と考えた場合 \(8b-4b=4b\) と同じと考えることができます。
無理数の掛け算
■ 掛け算の場合も 文字 の 掛け算 と同じと考える
- 無理数 × 有理数
- 有理数 × 無理数
- 無理数 × 無理数 という計算ができます。
■ 例題 掛け算
\(3×\sqrt2=3\sqrt2\) は \(3×a=3a\) と同じ。
\(\sqrt2×\sqrt5=\sqrt{10}\) は \(a×b=ab\) と同じ。
無理数の割り算
■ 割り算の場合も 文字 の 割り算 と同じと考える
- 無理数 ÷ 有理数
- 有理数 ÷ 無理数
- 無理数 ÷ 無理数 という計算ができます。
注意するのは、分母に無理数が残ってはいけないので、その場合には 分母の有理化 をしなければならないことです。
■ 例題 割り算
\(8\sqrt2÷2=4\sqrt2\) は \(8a÷2=4a\) と同じ。
\(\sqrt{14}÷\sqrt7=\sqrt{2×7}÷\sqrt7=\sqrt2\) は \(a×c÷c=a\) と同じ。
■ 分母に無理数が残る場合はそのままではいけません。
この場合は 分母の有理化 をする必要があります。
\(\cfrac{3}{\sqrt2}=\cfrac{3}{\sqrt2}×\cfrac{\sqrt2}{\sqrt2}=\cfrac{3\sqrt2}{2}\)
で分母から無理数が消えました。
これが 分母の有理化 です。
整式の微分
微分するということは、どういうことかというと、関数 \(f(x)\) の導関数 \(f'(x)\) を求めることです。
これを関数 \(f(x)\) を微分するという。
■ 関数とは何か
関数とは対応である といった先生がいます。
つまり、 \(x\) を決めると、ひとつの \(y\) が決まることです。
たとえば、 \(y=x\) でも \(y=x^2\) でも \(x\) の値が決まると一つの \(y\) が決まります。
\(x\) に対応して \(y\) が決まるので 関数 と言えます。
変数 \(x\) の値は、好きな様に決められるので、独立変数といい、 \(y\) は変数 \(x\) の値によって決められるので、従属変数 といいます。
整式の定義
ある幾つかの文字を含む式を加法・減法・乗法を使って整理して、分母あるいは根号の中に文字を含まないようにした代数式のことです。
要するに答えとしての形としては、 分数の分母に文字が残っていたり、根号(ルート)の中に文字が残っていてはいけない ということです。
■ \(y=f(x)\)の持つ意味
これから \(y=f(x)\) という式にあるように
\(f(x)\) というものがでてきます。
この \(f(x)\) の意味をよく理解しておかないと、後で分からなくなります。
この \(f(x)\) の意味は ここに 関数が入りますよ ということを示しているのです。
ですから、ここに \(x、x^2、(2x+2)\) のように関数が入るという意味を理解しておくと良いでしょう。
関数の極限
関数 \(y=f(x)\) について、変数 \(x\) が数 \(a\) 以外の値をとりながら \(a\) に近づくとき、\(y=f(x)\) の値が限りなく値 \(b\) に近づくとする。
このことを \(\lim_{x \to a} f(x)=b\) または \(\lim_{x \to a} y=b\)\(\cdots(1)\) と書きます。
\(lim\) はリミットとよみます。
\(x\) を限りなく \(a\) に近づけるとき \(y=f(x)\) は \(b\) に収束するといいます。
\(b\) を \(x\) が \(a\) に近づくときの \(y=f(x)\) の極限値といいます。
上の式(1)を次のように書くこともあります。
\(x→a\) のとき \(f(x)→b\) または \(f(x)→b (x→a)\) と書きます。
極限値の考え方はどうするか
■ 極限値の考え方
- 代入するということ
- 分数は約分してから
■ 例題
1.\(\lim_{h \to 1} (1+2h)\)\(=1+2×1=3\)\(\cdots h=1\) を代入
2.\(\lim_{h \to 0} (1+2h+h^2)\)\(=1+2×0+0^2=1\)\(\cdots h=0\) を代入
3.\(\lim_{h \to 1}\cfrac{3(a+h^2)-3a^2}{h}\)
\(=\lim_{h \to 1}\cfrac{3(a^2+2ah+h^2)-3a^2}{h}\)
\(=\lim_{h \to 1}\cfrac{6ah+3h^2}{h}\)
\(=\lim_{h \to 1}(6a+3h)=6a\)
4.\(\lim_{h \to 1}\cfrac{(3+h)^3-3^3}{h}\)
\(=\lim_{h \to 1}\cfrac{h^3+9h^2+27h-27}{h}\)
\(=\lim_{h \to 1}\cfrac{h^3+9h+27h}{h}\)
\(=\lim_{h \to 1}(h^2+9h+27)=27\)
5.\(\lim_{x \to 2} \cfrac{x^2+x-6}{x^2-4}\)
\(=\lim_{x \to 2}\cfrac{(x+3)(x-2)}{(x+2)(x-2)}\)
\(=\lim_{x \to 2}\cfrac{(x+3)}{(x+2)}\)
\(=\cfrac{5}{4}\)
■ 平均変化率とは傾きのこと
\(y=f(x)\) において、変数 \(x\) の値が \(a\) から \(b\) まで変化するとき、\(y\) は \(f(a)\) から \(f(b)\) まで変化する。
\(y\) の増分を \(⊿y=f(b)-f(a)\) で表し
\(x\) の増分を \(⊿x=b-a\) で表す。
⊿はデルタとよみます。
ここで、\(⊿y\) と \(⊿x\) の比のことを関数 \(y=f(x)\) の平均変化率をいう。
この平均変化率は傾きのことです。
\(\cfrac{⊿y}{⊿x}= \cfrac{f(b)-f(a)}{b-a} \cdots(2.1)\)
\(x\) の増分 \(⊿x=b-a\) から \(b=a+⊿x\) とすると
\(\therefore ⊿y=f(a+⊿x)-f(a)\) となり、平均変化率(2.1)は次のようになる。
\(\cfrac{⊿y}{⊿x}\)\(=\cfrac{f(a+⊿x)-f(a)}{⊿x}\cdots(2.2)\)
■ 例題
\(y=f(x)\) で \(y=2x^2\) のとき \(y’\) は
1.\(\cfrac{2×3^2-2×1^2}{3-1}\)\(=\cfrac{18×2}{2}=8\)
2.\(\cfrac{2(-1)^2-2(-4)^2}{-1-(-4)}\)\(=\cfrac{-30}{3}=-10\)
3.\(\cfrac{2b^2-2a^2}{b-a}\)
\(=\cfrac{2(b+a)(b-a)}{b-a}\)\(=2(a+b)\)
4.\(\cfrac{2(1+h)^2-2×1^2}{1+h-1}\)
\(=\cfrac{2h^2+4h+2-2}{h}\)
\(=\cfrac{2h^2+4h}{h}=2h+4\)
5.\(\cfrac{2(a+h)^2-2(a)^2}{a+h-a}\)
\(=\cfrac{2h^2+4ah+2a^2-2a^2}{h}\)
\(=\cfrac{2h^2+4ah}{h}=4a+2h\)
微分係数
■ 定義に従った求め方
微分係数=接線の傾き です。
関数 \(y=f(x)\) について、\(x\) が \(a\) から \(a+h\) まで変化すると、平均変化率は次のようになります。
\(\cfrac{⊿y}{⊿x}\)=\(\cfrac{f(a+h)-f(a)}{h}\)
定義に従った求め方というのは、平均変化率の極限値を求めることです。
その極限値のことを微分係数 という。
記号は \(f'(a)\) とする。
したがって、\(y=f(x)\) の \(x=a\) における微分係数は次のようになる。
\(f’\)の’(ダッシュ)が微分すること を意味します。
\(f'(a)=\lim_{h \to 0} \cfrac{f(a+h)-f(a)}{h} \cdots(2.3)\)
また、次のように表すこともできる。
\(f'(a)=\lim_{x \to a} \cfrac{f(x)-f(a)}{x-a} \cdots(2.4)\)
■ (f(3)) の意味は何かというと
\(y=f(x)=2x^2\) のときに
\(y=2x^2\) に \(x=3\) を入れた時の \(y\) の値はいくつかということを意味しています。
1.\(f(x)=2x^2\) で \(x=1\) とした時
\(f'(1)\)\(=\lim_{h \to 0}\cfrac{f(1+h)-f(1)}{1+h-1}\)
\(=\lim_{h \to 0}\cfrac{2(1+h)^2-2×1^2}{h}\)
\(=\lim_{h \to 0}\cfrac{2h^2+4h+2-2}{h}\)
\(=\lim_{h \to 0}\cfrac{h(2h+4)}{h}=4\)
2.\(f(x)=2x-3\) で \(x=-1\) とした時
\(f'(-1)\)\(=\lim_{h \to 0}\cfrac{f(-1+h)-f(-1)}{-1+h-(-1)}\)
\(= \lim_{h \to 0}\cfrac{\{(-2+2h)-3\}-\{2(-1)-3\}}{h}\)
\(=\lim_{h \to 0}\cfrac{2h}{h}\)
\(=\lim_{h \to 0}2=2\)
微分とは導関数を求めること
導関数は微分係数のときの \(a\) が \(x\) に変わっただけです。
そして、 導関数 \(f'(x)\) を求めることを微分する といいます。
■ 微分係数の変化
2次関数 \(f(x)=x^2\) の \(x=a\) における微分係数 \(f'(a)\) は
\(f'(a)=\lim_{⊿x \to 0} \cfrac{(a+⊿x)^2-a^2}{⊿x}\)
\(=\lim_{⊿x \to 0} \cfrac{a^2+2a⊿x+⊿x^2-a^2}{⊿x}\)
\(=\lim_{⊿x \to 0} \cfrac{⊿x(2a+⊿x)}{⊿x}\)
\(=\lim_{⊿x \to 0}(2a+⊿x)=2a\)
となリます。
ここで勘違いをするのが、\(⊿y\) の増加分の内の \(-a^2\) を忘れてしまうことです。
話を戻して、2次関数 \(f(x)=x^2\) の \(x=a\) における微分係数 \(f'(a)\) は \(f'(a)=2a\) となりますので、微分係数 \(f'(a)=2a\) は \(a\) が決まれば \(f'(a)\) が決まりますので \(a\) の関数であるといえます。
ここで、 \(a\) を \(x\) でおきかえれば、2次関数 \(f(x)=x^2\) から新たに関数 \(f'(x)=2x\) を作ることができる。
導関数の定義
一般に、関数 \(f(x)\) について、微分係数 \(f'(x)\) を 関数 \(f(x)\) の導関数といいます。
■ 導関数
関数 \(y=f(x)\) の導関数 \(f'(x)\) は
\(f'(x)=\lim_{⊿x \to 0} \cfrac{⊿y}{⊿x}\)\(=\lim_{⊿x \to 0} \cfrac{f(x+⊿x)-f(x)}{⊿x}\)
そして、関数 \(f(x)\) の導関数を
\(y’、f’、f'(x)、\frac{dy}{dx}、\frac{df}{dx}、\frac{d}{dx}f(x)\) などの記号で表す。
ここで、分子の \(f(x+⊿x)-f(x)\) を展開したくなるが、\(f(x+⊿x)\) 自体がひとつの関数なので、これ以上展開できないことを理解しなければならない。
微分
関数 \(f(x)\) の導関数 \(f'(x)\) を求めることを関数 \(f(x)\) を微分するという。
微分とは接線の傾きを求めることである。
参考
3乗の展開公式
\(( a+b)^3=a^3+3a^2b+3ab^2+b^3\)
\(( a-b)^3=a^3-3a^2b+3ab^2-b^3\)
\((a+b)(a^2- ab+b^2)= a^3+b^3\)
\((a-b)(a^2+ ab+b^2)= a^3-b^3\)
微分の公式(簡単な方法)
■ 微分の公式
前に出して、1次下げる。
\((x^n)’=nx^{n-1}\) (nは正の整数)
■ 例題
\((x^3)’=3×x^2=3x^2\)
\((3x^2)’=2×3x^1=6x\)
\((-5x)’=1×(-5)x^0=-5\)
\((7)’=0\)
三角関数の微分と積分の公式
三角関数の微分は、大ざっぱに言うと サインを微分するとコサイン< になり、 コサインを微分するとサイン になるということになります。
微分の公式
\((\sin x)’=\cos x\)
\((\cos x)’=-\sin x\)
\((\tan x)’=\cfrac{1}{\cos^2x}=\sec^2x\)
\(a\) を定数として、一般化する
\((\sin ax)’=a\cos ax\)
\((\cos ax)’=-a\sin ax\)
\((\tan ax)’=a\sec^2ax\)
積分の公式
\(\int \cos xdx=\sin x+C\)
\(\int \sin xdx=-\cos x+C\)
\(a\) を定数として、一般化する
\(\int \cos axdx=\cfrac{1}{a}\sin ax+C\)
\(\int \sin axdx=-\cfrac{1}{a}\cos ax+C\)
整式の積分
積分をするには、微分を知らないと積分をすることができません。
なぜなら、積分するとは微分の反対 をすることなのです。
積分のマークはインテグラルと読みます。
積分するとは、どういうことか
\(f(x)=x^2\) を微分すると、\(f'(x)=2x\) となる訳ですが、積分するとは微分して求めた式の元の式を求める ことです。
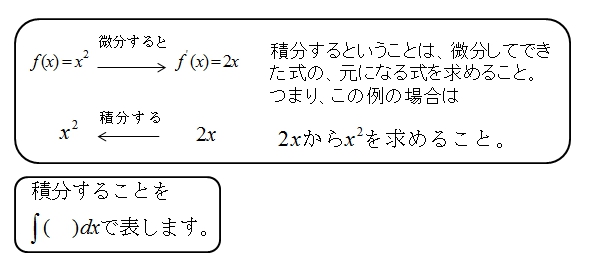
■ 微分する時
微分のときは「前に出して、1次下げる」といいました。
■ 積分する時
積分のときは「次数を上げて、次数を分母に置く」です。
例題
- \(\int x^2 dx=\cfrac{1}{3} x^3=\cfrac{x^3}{3}\)
- \(\int x dx=\cfrac{1}{2} x^2=\cfrac{x^2}{2}\)
- \(\int 1 dx=\cfrac{x}{1}=x\)
- \(\int kx dx=k\int x dx=k\cfrac{x^2}{2}\)
- \(\int A dx+\int B dx\)\(=\int(A+B) dx\)\(=\cfrac{(A+B)^2}{2}\)
不定積分とは
答えがひとつでなく、たくさんあって、ひとつに定まらないものです。
上の \(f(x)=x^2\) の微分して、\(2x\) になるのは \(x^2\) だけではなく
\(x^2+1\)
\(x^2+5\)
\(x^2-2\)
\(x^2+100・・・\) などのようにたくさんあります。
そのため、この数字にあたるものを 「積分定数C」 としています。
そのため、上の例の答えは「積分定数C」を付けなければならないのです。
次のようになります。
例題
- \(\int x^2 dx=\cfrac{1}{3} x^3=\cfrac{x^3}{3}+C\)
- \(\int x dx=\cfrac{1}{2} x^2=\cfrac{x^2}{2}+C\)
- \(\int 1 dx=\cfrac{x}{1}=x+C\)
- \(\int kx dx=k\int x dx=k\cfrac{x^2}{2}+C\)
- \(\int A dx+\int B dx\)\(=\int(A+B) dx\)\(=\cfrac{(A+B)^2}{2}+C\)
定積分
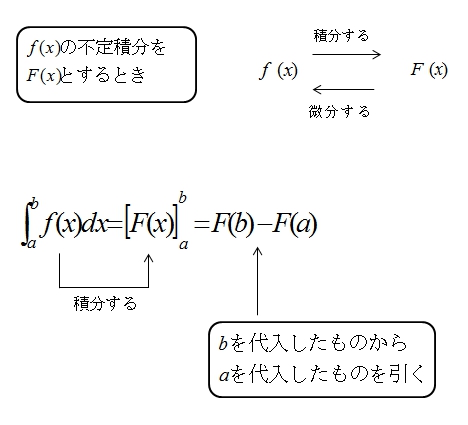
例題
1.\(\int^3_2 x dx=\left[\cfrac{x^2}{2} \right]^3_2\)
\(=\cfrac{3^2}{2}-\cfrac{2^2}{2}\)
\(=\cfrac{5}{2}\)
2.\(\int^2_{-1}(3x^2-5x+2) dx\)
\(=\left[x^3-\cfrac{5}{2}x^2+2x \right]^2_{-1}\)
\(=(2^3-\cfrac{5}{2}×2^2+2×2)\)\(-\{(-1)^3-\cfrac{5}{2}(-1)^2+2(-1)\}\)
\(=\cfrac{5}{2}\)
3.\(\int^2_1(x-3)(x+1) dx\)
\(=\int^2_1(x^2-2x-3) dx\)
\(=\left[\cfrac{x^3}{3}-x^2-3x \right]^2_1\)
\(=(\cfrac{2^3}{3}-2^2-2^2×3×2)\)\(-(\cfrac{1^3}{3}-1^2-3×1)\)
\(=-\cfrac{22}{3}-(-\cfrac{11}{3})\)
\(=-\cfrac{11}{3}\)
定積分についての公式

円
円周率が3.14・・・と続くのは誰でも知っていmasu .
では、円周率ってどうやって出すの?と聞かれて答えられる人はどれだけいるでしょう。
分からなかったので調べて見ました。
パイを習った時に3.14・・・と続くのは記憶があるが、 円周と直径の比率 ということはまるっきり覚えていません。
私だけか?
それくらい、数字のほうの印象が強いのではないでしょうか。
■ 円周と直径を測れば、円周 ÷ 直径で求めることができます。
\(π=\cfrac{円周}{直径}=\cfrac{2πr}{2r}=π\)
円の面積
■ 円の面積=\(πr^2\)=(円周÷2)×半径になる理由
図1のように円を半分にして、小さなピースに分けます。
ピースをものすごく小さくすると円周の曲線は直線になリます。
図1
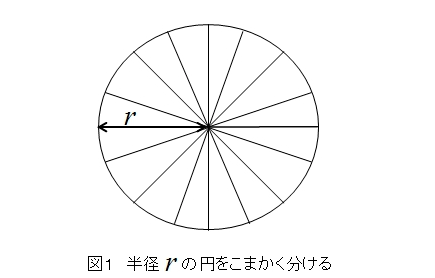
図2
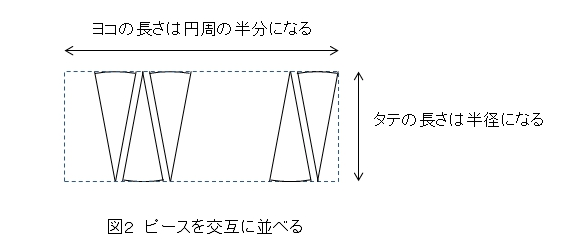
図2のようにこのピースを互い違いに並べると円は長方形になる。
ここで
円の面積=平行四辺形の面積
↓
円の面積=底辺×高さ
↓
円の面積=円周の半分×半径
上の式にそれぞれを当てはめると
円周は \(2πr\) ですから
円の面積=\(\cfrac{円周}{2}×半径=\cfrac{2πr}{2}×r=πr^2\) になります。