電池の内部抵抗とは、文字通り電池が内部に持つ抵抗のことをいいます。
理想的な電源とすれば電池の場合、内部抵抗が無いあるいは小さい方が電源としては適しています。
電池が持つ内部抵抗は、電池が新しいときはあまり問題になりませんが、電池が消耗してくると無視できなくなります。
ここでは、電池の内部抵抗と流れる電流によって、端子電圧がどのように変化するかを説明します。
電池の内部抵抗とは何か
電池には電流を流す元になる 起電力 \(E\) があります。
そして、電流が流れることにより発生する 内部抵抗 \(r\) があります。
電池の構造を電気回路として見る、と次のように考えることができます。

電池の起電力は、電池を使用することで徐々に小さくなって行きます。
これは、電池の元になる、化学変化ができなくなったり、何らかの事情で電池の内部抵抗が、徐々に大きくなることで電池の寿命が尽きるとも考えられます。

電池の内部抵抗と電気回路の関係
起電力 \(E\) の電池に、負荷抵抗 \(R\) を接続した回路に流れる電流を \(I\) とすると次のようになります。
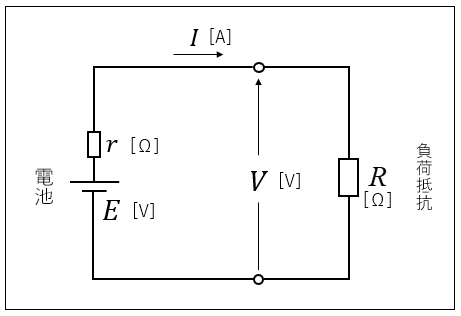
オームの法則から、それぞれの関係は
\(E=rI+V=(r+R)I\) [V]
\(V=E-rI\) [V]
電池を短絡した場合
電池を短絡するとどうなるでしょうか?
仮に、電池の内部抵抗を \(1.0\) [Ω] として考えてみます。
次の図から
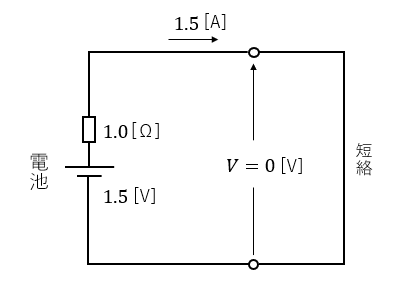
\(E=rI+V=(r+R)I\) [V]
\(I=\cfrac{1.5}{1.0}=1.5\) [A] になります。
短絡するので、負荷の端子電圧 \(V\) はゼロになります。
電池の寿命と端子電圧
電気製品に使用している電池がなくなって、電池をを入れ替えることがあります。
使い終わった電池の電圧を、テスターやバッテリーチェッカーで測ってみると電圧が \(1.5\) [V] 近くあったりします。
ではこの電池は使えるかというと、実際には使えないことがほとんどです。
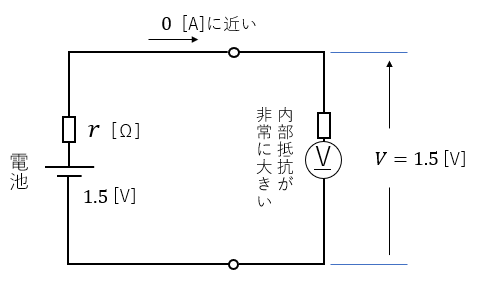
使い終わった電池の電圧が、\(1.5\) [V] 近くになる理由は次のようなことが考えられます。
- 電圧計の内部抵抗は非常に大きいため、流れる電流が十分に小さい。
- 流れる電流が十分に小さいため、内部抵抗による電圧降下が起こらないので起電力が測定される。
\(V=E-rI\) で \(rI≒0\) なので
\(V=E\) [V] が表示される。
電池の現状を知るには、ある程度の電流を流したときの状態を見ないと、電池が使えるものなのかどうかはわかりません。
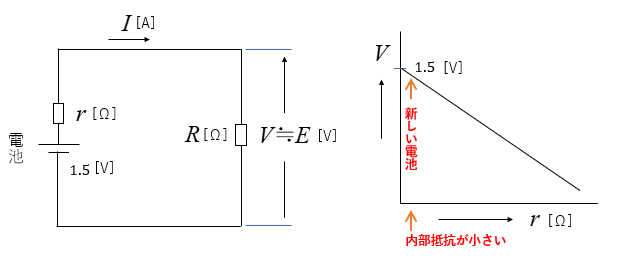
新しい電池のとき
端子電圧 \(V\) は
\(V=E-rI\) [V] になります。
ここで、新しい電池のときは、内部抵抗 \(r\) が非常に小さいので
\(V≒E\) [V] になります。
消耗した電池のとき
端子電圧 \(V\) は
\(V=E-rI\) [V] になります。
ここで、消耗した電池のときは、内部抵抗 \(r\) が大きくなっているので
\(rI\) [V] の電圧降下が無視できなくなります。

そのため、端子電圧 \(V\) は
起電力 \(E\) より、小さくなります。
練習問題
問題1
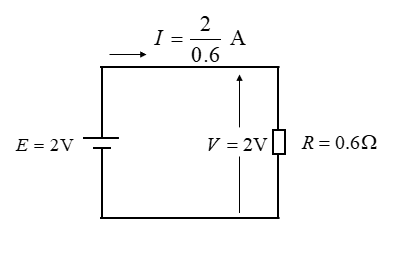
2 [V] の起電力がある電池に 0.6 [Ω] の抵抗を接続した回路があります。
抵抗の端子電圧を測定すると 1.5 [V] でした。
もし、端子を短絡すると 何 [A] の電流が流れるか求めよ。
(このような実験は危険なので行わないこと)
<解答例>
この問題は、電池には内部抵抗があるということを示しています。
■ 電池に内部抵抗がない場合
電池の電圧は、抵抗の電圧降下と同じになります。
■ 問題文の場合
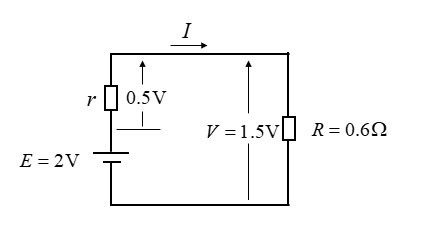
電池の内部抵抗を \(r\) とすると、負荷抵抗を \(R\) とすれば回路に流れる電流は
\(I=\cfrac{E}{r+R}\) [A]
抵抗 \(R\) の端子電圧は
\(V=RI=\cfrac{ER}{r+R}\) [V]
内部抵抗は
\(r=\cfrac{(E-V)R}{V}=\cfrac{0.5×0.6}{1.5}=0.2\) [Ω]
あるいは
\(V=E-rI=\cfrac{RE}{r+R}\) から \(r\) を求めます。
短絡時に流れる電流は
\(I_0=\cfrac{E}{r}=\cfrac{2}{0.2}=10\) [A] になります。
