ここでは、演算増幅器の説明をします。
演算増幅器(OPアンプ)
演算増幅器は オペアンプ(OPアンプ) ともいいます。
理想増幅器としての条件
理想増幅器としての条件は次のようなものです。
- \(Z_i=∞\) 入力インピーダンスが無限大
- \(Z_o=0\) 出力インピーダンスがゼロ
- \(A_v=∞\) 電圧増幅度無限大
- \(f\) 周波数特性が良い
- 雑音が少ない
演算増幅器(OPアンプ) は理想増幅器に近い特性を持っていて、音響機器やラジオ、テレビなどの電子機器によく使われています。
演算増幅器は、反転入力(-)と非反転入力(+)の2つの入力端子と、1つの出力端子をもつ増幅器です。
■ 反転入力端子を逆相入力端子
非反転入力端子 を 正相入力端子 と表現する場合もあるようです。
一般に、電源は正負の同じ大きさの2つの電源を必要として、\(\pm15\quad\rm[V]\) が使われる。
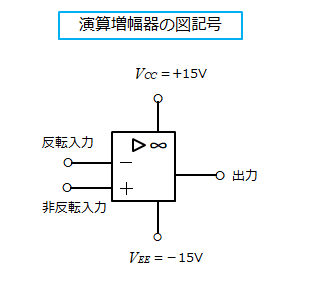
演算増幅器の特性
演算増幅器は、図のような理想増幅器と近い特性を持っています。
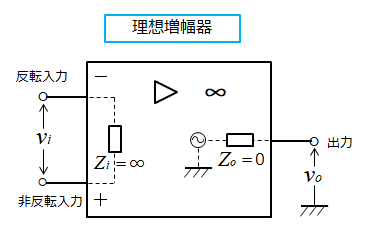
演算増幅器の
入力インピーダンス \(Z_i=∞\)
出力インピーダンス \(Z_o=0\)
電圧増幅度 \(A_v=∞\) と考えてみます。
\(A_v=\cfrac{v_o}{v_i}\) なので
\(v_i=\cfrac{v_o}{A_v}\) になる。
ここで、\(A_v=∞\) とすると
\(v_i≒0\quad\rm[V]\) となります。
この状態を、入力端子間が短絡しているように動作しますので、仮想的短絡(バーチャルショート) といいます。
演算増幅器の種類
■ 反転増幅回路
反転増幅回路とは、入力電圧と出力電圧の符号が反転するため、このように呼ばれます。
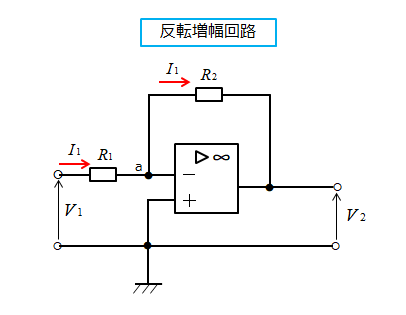
a 点は仮想的短絡なので、 \(0\) [V] と考えます。
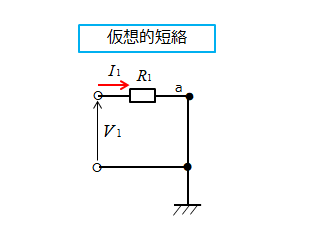
\(V_1=R_1I_1[V]\)
また、\(V_2\) は
\(V_2=-R_2I_1\) [V] となります。
マイナスになる理由は、次の記事を参照してください。
反転増幅回路の電圧増幅度は、上の式から次のようになります。
\(A_v=\cfrac{V_2}{V_1}=-\cfrac{R_2}{R_1}\)
■ 非反転増幅回路
非反転増幅回路とは、入力電圧と出力電圧の符号が同じになります。
そのため、このように呼ばれます。
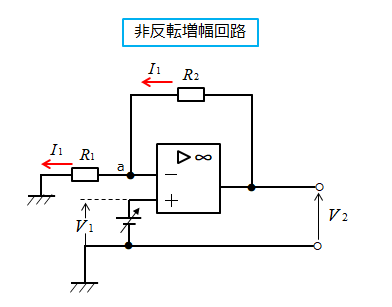
a 点は仮想的短絡なので、\(V_1\) と考えます。
\(R_1I_1=V_1\)
\((R_1+R_2)I_1=V_2\) なので
\(A_v=\cfrac{V_2}{V_1}=\cfrac{(R_1+R_2)I_1}{R_1I_1}\)
非反転増幅回路の電圧増幅度は、次のようになります。
\(A_v=\cfrac{V_2}{V_1}=1+\cfrac{R_2}{R_1}\)
練習問題
問題1
図のような直流増幅回路の出力電圧 \(V_2\) [V] を求めよ。
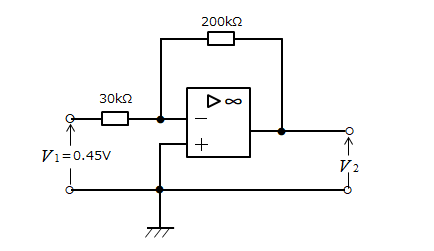
<解 答>
この回路は、反転増幅回路なので
\(A_v=\cfrac{V_2}{V_1}=-\cfrac{R_2}{R_1}\) にそれぞれの数値を代入します。
\(A_v=\cfrac{V_2}{0.45}=-\cfrac{200kΩ}{30kΩ}=-\cfrac{20}{3}\)
\(V_2=-\cfrac{20}{3}×0.45=-3.0\) [V]
問題2
図のような直流増幅回路の出力電圧 \(V_2\) [V] を求めよ。
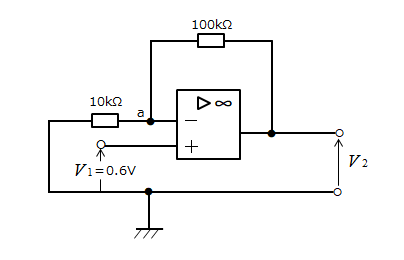
<解 答>
この回路は、非反転増幅回路なので
\(A_v=\cfrac{V_2}{V_1}=1+\cfrac{R_2}{R_1}\) にそれぞれの数値を代入します。
\(A_v=\cfrac{V_2}{0.6}=1+\cfrac{100kΩ}{10kΩ}=11\)
\(V_2=0.6×11=6.6\) [V] になります。
