インピーダンスは、分かったようで分からないような、少しややこしい用語です。
インピーダンスとは 交流回路における抵抗のような働きをするもの で単位も抵抗と同じ オーム [Ω] を使います。
実際に インピーダンスの計算をしようとすると、どのように計算したらよいか考えてしまうのではないでしょうか?
特に、複素数が入ってきて 記号法 で計算するとなると分かりづらくなります。
ここでは、インピーダンスの計算について、問題を解きます。
RLC回路とインピーダンス
RLC直列回路のまとめ
RLC直列回路の「インピーダンス、流れる電流、端子電圧」を求める公式のまとめです。
| RLC直列回路 | 公式 | |
|---|---|---|
| インピーダンス | 記号法 | \(Z=R+j(X_L-X_C)\) [Ω] |
| 大きさ | \(Z=\sqrt{R^2+X^2}\) [Ω] | |
| \(Z=\sqrt{R^2+(X_L-X_C)^2}\) [Ω] | ||
| 流れる電流 | 大きさ | \(I=\cfrac{E}{Z}\) [A] |
| \(I=\cfrac{E}{\sqrt{R^2+(ωL-\cfrac{1}{ωC})^2}}\) [A] | ||
| \(I=\sqrt{{I_R}^2+{I_X}^2}\) [A] | ||
| \(I=\sqrt{{I_R}^2+(I_L-I_C)^2}\) [A] | ||
| 端子電圧 | 大きさ | \(V_R=RI\) [V] |
| \(V_L=X_LI\) [V] | ||
| \(V_C=X_CI\) [V] | ||
RLC並列回路のまとめ
RLC並列回路の「インピーダンス、流れる電流、端子電圧」を求める公式のまとめです。
| RLC並列回路 | 公式 | |
|---|---|---|
| インピーダンス | 記号法 | \(\cfrac{1}{Z}=\cfrac{1}{R}+\cfrac{1}{jX_L}+\cfrac{1}{-jX_C}\) [Ω] 最終的には \(Z=\) として求める。 |
| 流れる電流 | 記号法 | \(I=E\left(\cfrac{1}{R}+\cfrac{1}{jX_L}+\cfrac{1}{-jX_C}\right)\) [A] |
| 大きさ | \(I=\sqrt{{I_R}^2+(I_L-I_C)^2}\) [A] | |
| 素子を流れる電流 | 記号法 | \(I_R=\cfrac{E}{R}\) [A] |
| \(I_L=\cfrac{E}{jX_L}\) [A] | ||
| \(I_C=\cfrac{E}{-jX_C}\) [A] | ||
| 大きさ | \(I_R=\cfrac{E}{R}\) [A] | |
| \(I_L=\cfrac{E}{X_L}\) [A] | ||
| \(I_C=\cfrac{E}{X_C}\) [A] | ||
練習問題
問題1
12Ωの抵抗と5Ωの誘導性リアクタンスが、直列に接続されています。
抵抗とコイルの合成インピーダンスを求めよ。
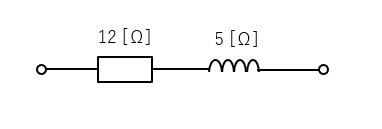
<解答例>
この問題は インピーダンスの大きさを求めれば良いので、数値を代入すれば OKです。
RLC直列回路の公式に数値を代入します。
\(Z=\sqrt{R^2+X^2}\)
\(Z=\sqrt{12^2+5^2}=13\) [Ω] になります。
問題2
交流電源100Vに、4Ωの抵抗と3Ωの誘導性リアクタンスが、直列に接続されています。
回路の抵抗とコイルにかかる電圧を求めよ。
また、電圧のベクトル図を描きなさい。
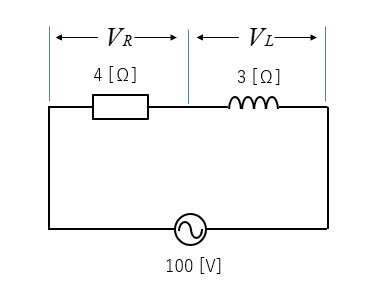
<解答例>
この問題は、回路に流れる電流を求めれば解けます。
RLC直列回路の公式から、合成インピーダンス \(Z\) は
\(Z=\sqrt{R^2+X^2}\) なので、数値を代入すると
\(Z=\sqrt{4^2+3^2}=5\) [Ω]
回路に流れる電流 \(I\) は
\(I=\cfrac{100}{5}=20\) [A] になります。
したがって
\(V_R=4×20=80\) [V]
\(V_L=3×20=60\) [V]
コイルの電圧は 電流に対して \(\cfrac{π}{2}\) 進みます。
ベクトル図は次のようになります。
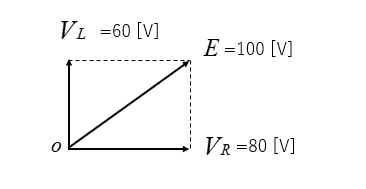
\(E=\sqrt{80^2+60^2}=100\) [V] となり、電源電圧と等しくなります。
問題3
交流電源100Vに、40Ωの抵抗と80Ωの誘導性リアクタンス、50Ωの容量性リアクタンスが
直列に接続されています。
回路の合成インピーダンス \(Z\) [Ω] と
回路に流れる電流 \(I\) [A] を求めよ。
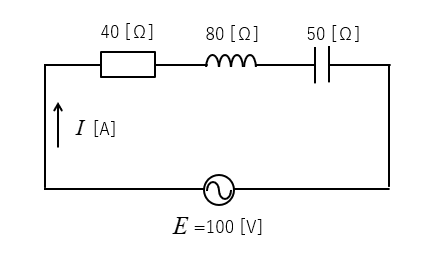
<解答例>
回路のインピーダンスを求める公式は
\(Z=\sqrt{R^2+X^2}\)\(=\sqrt{R^2+(X_L-X_C)^2}\)
\(Z=\sqrt{40^2+(80-50)^2}=50\) [Ω] になります。
また、電流 \(I\) は
\(I=\cfrac{E}{Z}=\cfrac{100}{50}=2\) [A] となります。
問題4
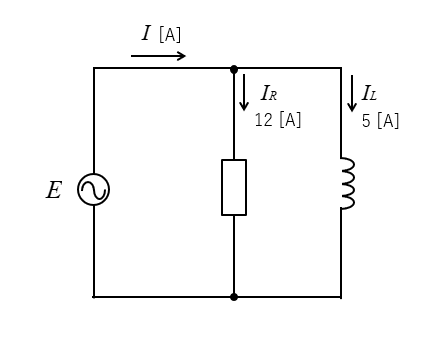
抵抗と誘導性リアクタンスが、並列に接続されています。
抵抗を流れる電流は、12A
誘導性リアクタンスを流れる電流は、5Aです。
回路に流れる電流 \(I\) [A] を求めよ。
<解答例>
並列回路の電流の大きさは
\(I=\sqrt{{I_R}^2+{I_L}^2}\) なので
\(I=\sqrt{12^2+5^2}=13\) [A] になります。
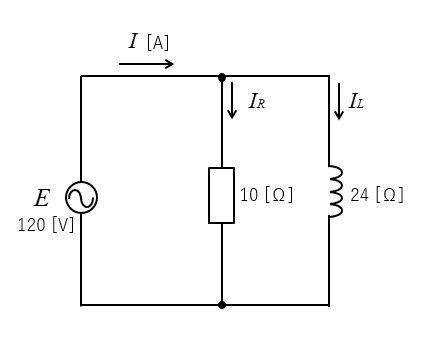
また、この問題が図のように、
電源電圧120V、抵抗10Ω、リアクタンス24Ωの場合の電流を求めよ。
<解答例>
RLC並列回路の公式から
インピーダンスの逆数は、各インピーダンスの逆数の和になります。
\(\cfrac{1}{Z}=\cfrac{1}{10}+\cfrac{1}{j24}\)
並列回路の電流は
\(I=\cfrac{E}{Z}\) なので
\(I=120×(\cfrac{1}{10}+\cfrac{1}{j24})\)\(=12-j5\) [A]
並列回路の電流の大きさは
\(I=\sqrt{{I_R}^2+{I_L}^2}\) なので
\(I=\sqrt{12^2+5^2}=13\) [A] になります。
問題5
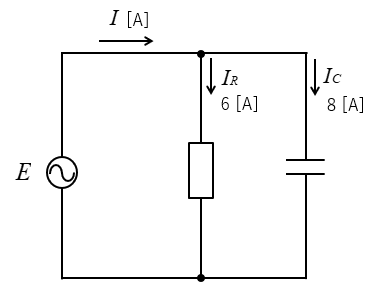
抵抗とコンデンサの並列回路です。
抵抗を流れる電流は、6A
容量性リアクタンスを流れる電流は、8Aです。
回路に流れる電流 \(I\) を求めよ。
<解答例>
RLC並列回路の公式から
並列回路の電流の大きさは
\(I=\sqrt{{I_R}^2+{I_C}^2}\) なので
\(I=\sqrt{6^2+8^2}=10\) [A] になります。
問題6
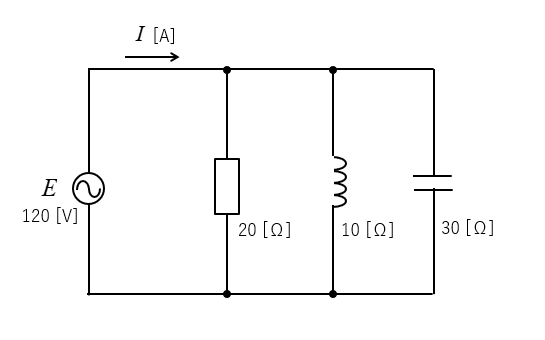
交流電源120Vに、20Ωの抵抗と10Ωの誘導性リアクタンス、30Ωの容量性リアクタンスが
並列に接続されています。
回路を流れる電流 \(I\) [A] を求めよ。
<解答例>
抵抗を流れる電流を \(I_R\) コイルを流れる電流を \(I_L\)
コンデンサを流れる電流を \(I_C\) とした回路図は 次のようになります。
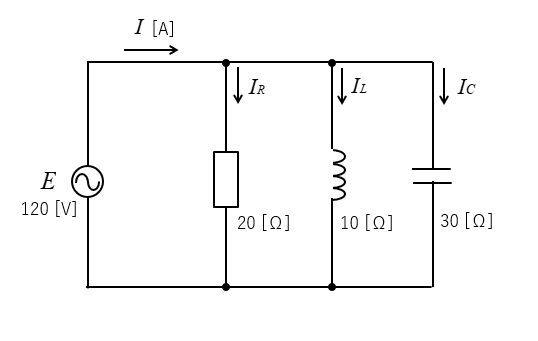
RLC並列回路の公式から
\(I_R=\cfrac{E}{R}\)\(=\cfrac{120}{20}=6\) [A]
\(I_L=\cfrac{E}{X_L}\)\(=\cfrac{120}{10}=12\) [A]
\(I_C=\cfrac{E}{X_C}\)\(=\cfrac{120}{30}=4\) [A]
ベクトル図は 次のようになります。
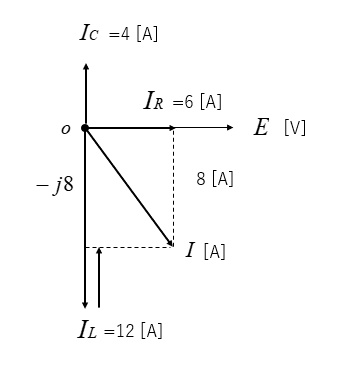
回路の電流 \(I\) [A] は
\(I=\sqrt{6^2+8^2}=10\) [A] になります。
<解答例>
■ アドミタンスを使って求める
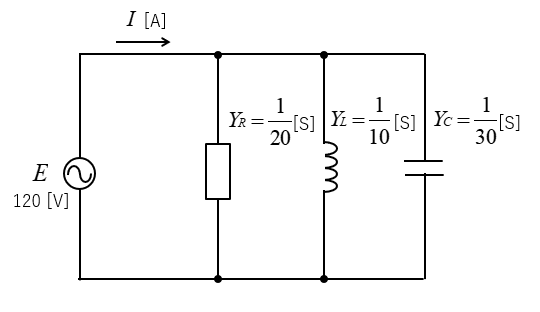
アドミタンス を \(Y\) [S] とすると
\(Y=Y_R+Y_L+Y_C\)
\(Y=\cfrac{1}{20}+\cfrac{1}{j10}-\cfrac{1}{j30}\)
\(Y=\cfrac{1}{20}-j\cfrac{2}{30}\) [S]
回路の電流 \(I\) [A] は
\(I=YE\)
\(I=(\cfrac{1}{20}-j\cfrac{2}{30})×120\)
\(I=6-j8\) [A] なので
回路の電流 \(I\) の大きさは
\(I=\sqrt{6^2+8^2}=10\) [A] となります。
問題7
抵抗と誘導性リアクタンスが、直列に接続されています。
電源電圧 \(100\) [V] で位相ゼロ、回路に \(10∠-\cfrac{\pi}{6}\) [rad] の電流が流れています。
この回路のインピーダンス \(Z、R、X_L\) を求めよ。
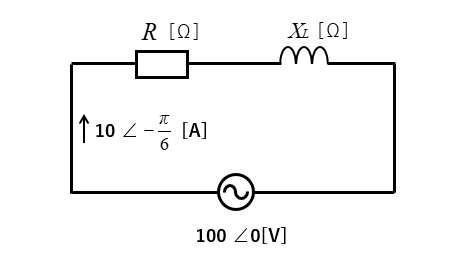
<解答例>
電圧と電流のベクトルを描くと、次のようになります。
電流は電圧より \(\cfrac{\pi}{6}\) 遅れています。
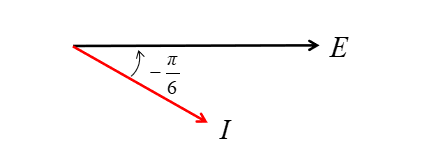
RL直列回路では、電流を基準にして \(V_R、V_L\) を描くとわかりやすくなります。
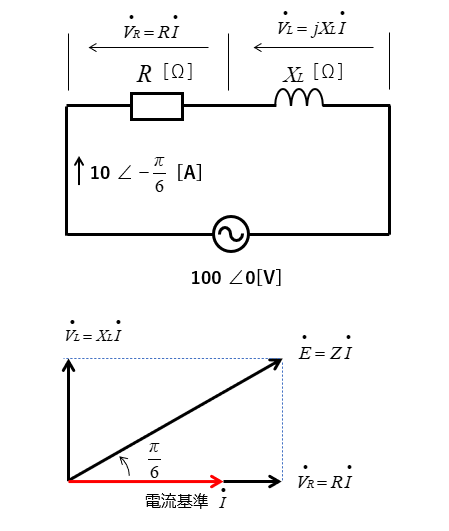
電圧のベクトル図から、インピーダンスの三角形が得られます。
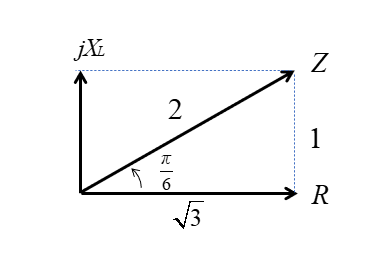
それぞれの辺の比は角度が \(\cfrac{\pi}{6}\) なので \(1:2:\sqrt3\) になります。
\(Z=\cfrac{E}{I}=\cfrac{100}{10}=10\) [Ω]
\(R=Z\cos\cfrac{\pi}{6}=10×\cfrac{\sqrt3}{2}=5\sqrt3\)
\(X_L=Z\sin\cfrac{\pi}{6}=10×\cfrac{1}{2}=5\)
したがって
\(Z=10\) [Ω]
\(R=5\sqrt3\) [Ω]
\(X_L=5\) [Ω] になります。
抵抗とコイルのインピーダンス計算
図のような抵抗とコイルの直列接続の、インピーダンス \(Z\) は次のようになります。
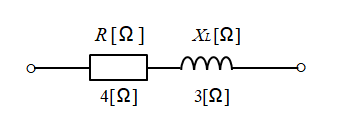
\(Z=R+jX_L\) (+jになることに注意)
\(|Z|=\sqrt{R^2+{X_L}^2}\)
ここで \(R=4\) [Ω] \(X_L=3\) [Ω] とすると
\(Z=4+j3\)
\(|Z|=\sqrt{4^2+3^2}=\sqrt{25}=5\) [Ω] になります。
★ ベクトル図
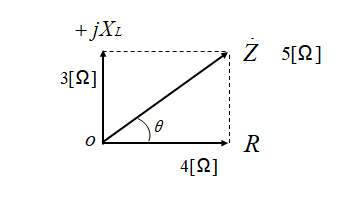
抵抗とコンデンサのインピーダンス
図のような抵抗とコンデンサの直列接続の インピーダンス \(Z\) を求めてみます。
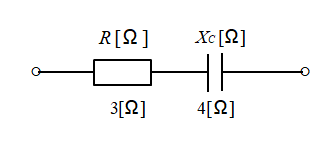
\(Z=R-jX_C\) (-jになることに注意)
\(|Z|=\sqrt{R^2+{X_C}^2}\)
ここで、\(R=3\quad\rm[Ω]\)、\(X_C=4\) [Ω] とすると
\(Z=3-j4\)
\(|Z|=\sqrt{3^2+4^2}=\sqrt{25}=5\) [Ω] になります。
■ ベクトル図
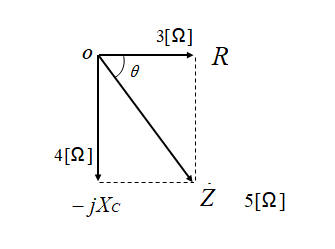
上記の問題にある、「抵抗とコイル」、「抵抗とコンデンサ」のインピーダンスの絶対値は、同じですがインピーダンスの位相は全く異なります。
インピーダンスの並列接続の計算
インピーダンスの並列接続の計算は 次のようにします。
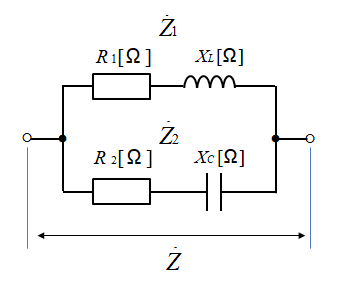
\(\cfrac{1}{Z}\)\(=\cfrac{1}{Z_1}+\cfrac{1}{Z_2}\)
\(\cfrac{1}{Z}\)\(=\cfrac{1}{R_1+jX_L}+\cfrac{1}{R_2-jX_C}\)
次のような、値が入っている時の計算です。
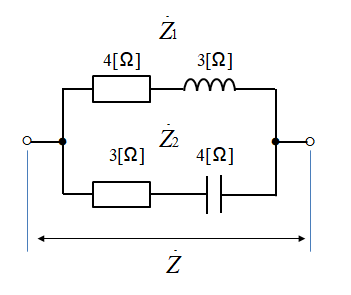
\(\cfrac{1}{Z}\)\(=\cfrac{1}{4+j3}+\cfrac{1}{3-j4}\)
逆数から、\(Z\) を求めて計算することができますが
並列回路の場合は アドミタンス として、逆数のままで計算する方が簡単になることがあります。
以上で「インピーダンスの計算」の説明を終わります。